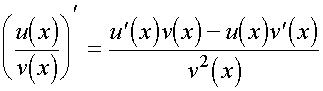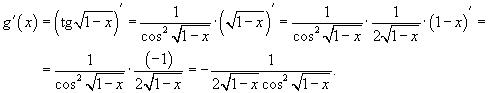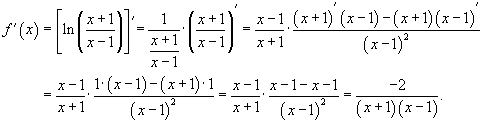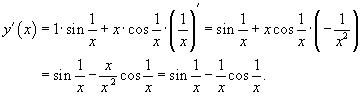18. Производная функции в точке, ее геометрический смысл. Сделай пожалуста и этот вопрос.

Геометрический смысл производной. Тангенс угла наклона касательной (угловой коэффициент наклона касательной), проведенной к графику функции в точке равен производной функции в этой точке: Заметим, что угол – это угол между прямой и положительным направлением оси ОХ: Уравнение касательной к графику функции в точке имеет вид: В этом уравнении: – абсцисса точки касания, – значение функции в точке касания, – значение производной функции в точке касания.

19.Свойства производной функции.

ПРОИЗВОДНАЯ ФУНКЦИИ

Рассмотрим произвольную внутреннюю точку x0 области определения функции y = f(x).

Разность

где x - также внутренняя точка области определения, называется

приращением аргумента в точке x0. Разность

называется

приращением функции в точке x0, соответствующим приращению

и обозначается

  

Производной функции y = f(x) в точке x0 называется предел отношения приращения

функции к приращению аргумента в этой точке при стремлении приращения аргумента к нулю, если такой предел существует и конечен, т.е.

 

ОСНОВНЫЕ СВОЙСТВА ПРОИЗВОДНЫХ

Если в точке x существуют конечные производные функций v = v(x) и u = u(x),

то в этой точке существуют также производные суммы, разности, произведения и частного этих функций, причем:

1.
2.
3.
4.			(при		);
5.

 

1. Производная сложной функции

Если функция y = f(x) имеет производную в точке x0, а функция y = g(x) имеет производную

в точке y0 = f(x0), то сложная функция h(x) = g(f(x))

также имеет производную в точке x₀, причем

2. Достаточное условие монотонности функции

Если в каждой точке интервала (a; b) выполнено неравенство

то функция y = f(x) возрастает на этом интервале.

 

Если

при

то y = f(x) убывает на (a; b).

3. Необходимое условие экстремума функции

Если точка x0 является точкой экстремума функции y = f(x) и в этой точке

существует производная

то она равна нулю

.

4. Признак максимума функции

Если функция y = f(x) определена на интервале (a; b), непрерывна в точке

имеет производную

на интервалах

и

на интервале

и

на интервале

то точка

x0 является точкой максимума функции

 

5. Признак минимума функции

Если функция

определена на интервале

непрерывна в

точке

имеет производную

на интервалах

и

на интервале

и

на интервале

то точка x0 является точкой минимума функции

 

Правило отыскания наибольшего и наименьшего значений функции.

Чтобы найти наибольшее и наименьшее значения функции, имеющей на отрезке конечное число критических точек (точек из области определения, в которых производная функции обращается в ноль или не существует), нужно вычислить значения функции во всех критических точках и на концах отрезка и выбрать наибольшее и наименьшее из полученных чисел.

20. Производные основных элементарных функций.

Производные тригонометрических функций (sin х)' = cos x, (cos х)' = -sin х,

Производную у = sin x найдем с помощью определения производной и I замечательного предела:

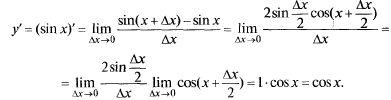
Производная у = cos х находится с помощью формул приведения и производной функции:

Производные у = tg х, у = ctg x могут быть найдены как производные частного. Например,

Производные обратных тригонометрических функций:

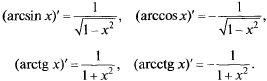
Т: Пусть функциявозрастает (убывает) на

 дифференцируема внутри промежутка иТогда существует возрастающая (убывающая) надиф-

ференцируемая обратная кфункцияпричем

Первая часть теоремы о существовании непрерывной функциигеометрически очевидна (рис. 9.3).

Выведем формулу для производной. По определению

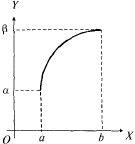
Рис. 9.3

В цепочке равенств использовали — непрерывна).

Получим теперь формулу для производной функции у = arcsin х.

Рассмотрим главное значение функции:Она является

обратной к х = sin у, которая возрастает и дифференцируема на

 причемПо теореме об обратной

функции имеем

Найдем формулу для производной у = arctg x, главное значение которойПользуясь теоремой об обратной функции, получаем

Для функций у = arcccos х, у = arcctg х производим аналогичные действия.

21. Производная сложной функции

"Двухслойная" сложная функция записывается в виде где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f.  Если f и g - дифференцируемые функции, то сложная функция также дифференцируема поx и ее производная равна Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - в точке u = g(x)!  Эта формула легко обобщается на случай, когда сложная функция состоит из нескольких "слоев", вложенных иерархически друг в друга.  Рассмотрим несколько примеров, иллюстрирующих правило производной сложной функции. Это правило широко применяется и во многих других задачах раздела "Дифференцирование".

Пример 1

Найти производную функции . Решение. Поскольку , то по правилу производной сложной функции получаем

Пример 2

Найти производную функции . Решение. Здесь мы имеем дело с композицией трех функций. Производная тангенса равна . Тогда

Пример 3

Определить производную функции . Решение. Применим формулы производной сложной функции и производной частного.

Пример 4

Продифференцировать функцию . Решение. Сначала найдем производную произведения:        Далее, по формуле производной сложной функции

Пример 5

Продифференцировать . Решение. Здесь мы опять имеем дело с "трехслойной" функцией. Поэтому дважды применяем формулу производной сложной функции. Получаем

22. Понятие дифференциала функции, его геометрический смысл и его свойства.

Дифференциалом функции вназывается главная, линейная относительно, часть приращения функции.

.

Покажем, что иэквивалентные бесконечно малые при:

(- бесконечно малая).

Геометрический смысл дифференциала:

Проведем к графику функции в точкукасательную и рассмотрим ординату этой касательной для точки . На рисунке,. Из прямоугольного треугольникаимеем:, т.е.. Но, согласно геометрическому смыслу производной,. Поэтомуили. Это означает, что дифференциал функциивравен приращению ординаты касательной к графику функции в этой точке, когдаполучает приращение.

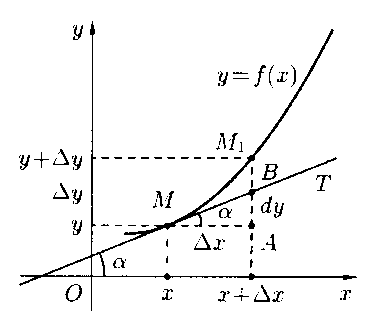
Приближенные вычисления:

Дифференциал функции обладает свойствами, аналогичными свойствам производной.

1. Дифференциал постоянной равен нулю: dc = 0, с = const.

2. Дифференциал суммы дифференцируемых функций равен сумме дифференциалов слагаемых:

d(u+v)=du + dv

Следствие. Если две дифференцируемые функции отличаются постоянным слагаемым, то их дифференциалы равны

d(u+c) = du (c= const).

3. Дифференциал произведения двух дифференцируемых функций равен произведению первой функции на дифференциал второй плюс произведение второй на дифференциал первой:

d(uv) = udv + vdu.

Следствие. Постоянный множитель можно выносить за знак дифференциала

d(cu) = cdu (с = const).

4. Дифференциал частного u/v двух дифференцируемых функций и = и(х) и v = v(x) определяется формулой

Пример . Пользуясь понятием дифференциала, вычислить приближенно ln 1,01.

Решение. Число ln 1,01 является одним из значений функции y = ln x . Формула (15) в данном случае примет вид

Положим

тогда

Следовательно,

что является очень хорошим приближением: табличное значение ln 1,01 = 0,0100.