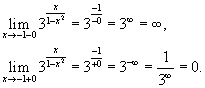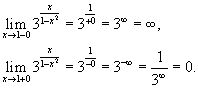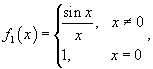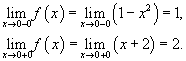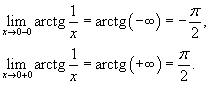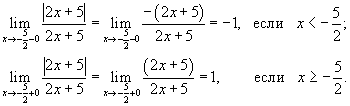15.Непрерывность сложных и обратных функций
Теорема (о
непрерывности сложной функции). Пусть
функция 
непрерывна
в точке
,
а функция
непрерывна
в точке
.
Тогда сложная функция
непрерывна
в точке
.
Всевозможные
арифметические комбинации простейших
элементарных функций, которые рассматривают
в школьном курсе алгебры и начал анализа,
мы будем называть элементарными
функциями. Например, 
является
элементарной.
Все
элементарные функции непрерывны в
области определения. Так что 
всюду
непрерывна, так как всюду определена,
а функция
разрывна
в точке 
.
Дадим теперь классификацию точек разрыва функции. Возможны следующие случаи.
1.
Если 
и
существуют
и конечны, но не равны друг другу, то
точку
называют
точкой разрыва первого рода. При этом
величину
называют
скачком функции в точке
.
Пример. Исследовать на непрерывность функцию
Решение. Эта
функция может претерпевать разрыв
только в точке 
,
где происходит переход от одного
аналитического выражения к другому, а
в остальных точках области определения
функция непрерывна.
Найдем
левосторонний предел функции при 
.
Cлева от точки
,
т.е. при
,
а
.
Справа
от точки 
.
Тогда
.
Значение функции в точке
,
т.е.
.
Функция в точке
имеет
разрыв первого рода. Это видно и на
графике функции (рис. 25).
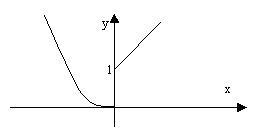
Рис. 25
2.
Если в точке 
,
но в точке
функция
либо
не определена, либо
,
то точка
является
точкой устранимого разрыва.
Последнее
объясняется тем, что если в этом случае
доопределить или видоизменить функцию 
,
положив
,
то получится непрерывная в точке
функция.
Пример. Функция 
в
точке
не
определена, но
,
т.е.
.
Доопределим функцию в точке 1, положив
ее значение в этой точке равным трем.
Тогда функция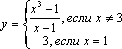
становится
непрерывной в точке
.
3. Точка разрыва функции, не являющаяся точкой разрыва первого рода или точкой устранимого разрыва, является точкой разрыва второго рода.
Пример. Функция 
в
точке
имеет
разрыв второго рода, так как
и
.
Пример. Исследовать
на непрерывность функцию 
.
Решение. Функция
не определена в точке 
.
Тогда
,
.
И функция в точке
имеет
разрыв второго рода.
Замечание. В
последних двух примерах мы ввели
символическую запись 
которая
означает, что знаменатель такой дроби
стремится к нулю, вся дробь стремится
к бесконечности, но вовсе не означает,
что мы производим деление на 0, что
невозможно.
|
| |||||||||||||||
|
16. Точки разрыва функции | |||||||||||||||
|
| |||||||||||||||
|
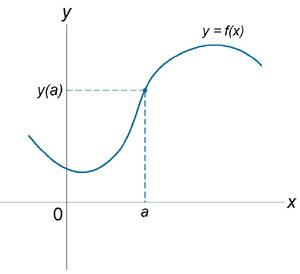
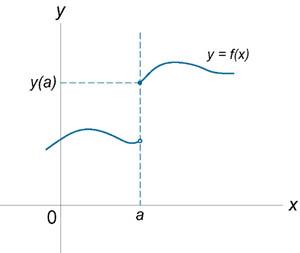
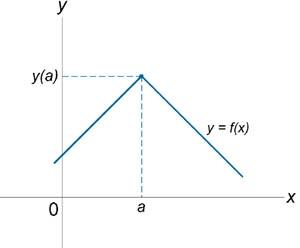
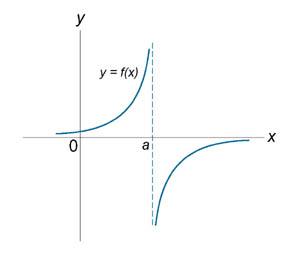
Если функция f (x) не является непрерывной в точке x = a, то говорят, что f (x) имеет разрыв в этой точке. На рисунке 1 схематически изображены графики четырех функций, две из которых непрерывны при x = a, а две имеют разрыв.
Классификация точек разрыва функции Все точки разрыва функции разделяются на точки разрыва первого и второго рода. Говорят, что функция f (x) имеет точку разрыва первого рода при x = a, если в это точке
При этом возможно следующие два случая:
Такая точка называется точкой устранимого разрыва.
Такая
точка называется точкой
конечного разрыва.
Модуль разности значений односторонних
пределов Функция f (x) имеет точку разрыва второго рода при x = a, если по крайней мере один из односторонних пределов не существует или равен бесконечности. | |||||||||||||||
|
Пример 1 | |||||||||||||||
|
| |||||||||||||||
|
Исследовать
функцию Данная функция не определена в точках x = −1 и x = 1. Следовательно, функция имеет разрывы в точкахx = ±1. Чтобы определить тип разрыва, вычислим односторонние пределы в этих точках. Поскольку левосторонний предел при x = −1 равен бесконечности, то данная точка является точкой разрыва второго рода. Аналогично, левосторонний предел в точке x = 1 равен бесконечности. Эта точка также является точкой разрыва второго рода. | |||||||||||||||
|
Пример 2 | |||||||||||||||
|
| |||||||||||||||
|
Показать,
что функция Решение. Очевидно,
данная функция не определена при x
= 0.
Поскольку sin x является
непрерывной функцией для всехx,
то искомая функция которая будет непрерывной при любом действительном x. | |||||||||||||||
|
Пример 3 | |||||||||||||||
|
| |||||||||||||||
|
Найти
точки разрыва функции Данная функция существует при всех значениях x, однако она состоит из двух различных функций и, поэтому, не является элементарной. Исследуем "поведение" этой функции вблизи точки x = 0, где ее аналитическое выражение изменяется. Вычислим односторонние пределеы при x = 0. Следовательно, функция имеет точку разрыва первого рода при x = 0. Скачок функции в этой точке равен При всех других значениях x функция является непрерывной, поскольку обе составляющие функции слева и справа от точки x = 0 представляют собой элементарные функции без точек разрыва. | |||||||||||||||
|
Пример 4 | |||||||||||||||
|
| |||||||||||||||
|
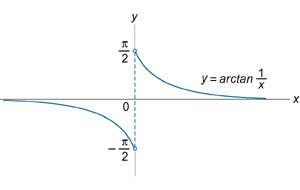
Найти
точки разрыва функции Решение. Данная элементарная функция определена для всех x, исключая точку x = 0, где она имеет разрыв. Найдем односторонние пределы в этой точке. Видно, что в точке x = 0 существует разрыв первого рода (рисунок 2).
| |||||||||||||||
|
Пример 5 | |||||||||||||||
|
| |||||||||||||||
|
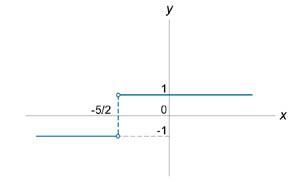
Найти
точки разрыва функции Решение. Функция
определена и непрерывна при всех x,
за исключением точки Так
как значения односторонних пределов
конечны, то, следовательно, в
точке | |||||||||||||||
и
правосторонний предел
;
называетсяскачком
функции.
на
непрерывность.
Решение.
имеет
устранимый разрыв в точкеx
= 0.
также
непрерывна при всехx за
исключением точки x
= 0.
Так
как 
,
то в данной точке существует устранимый
разрыв. Мы можем сконструировать новую
функцию
,
если они существуют.
Решение.
,
если они существуют.
,
если таковые существуют.
,
где существует разрыв. Исследуем точку
разрыва.
существует
разрыв первого рода. График функции
схематически показан на рисунке 3.