14.Предел последовательности комплексных чисел.

Определение

Число называетсяпределом числовой последовательности , если последовательностьявляется бесконечно малой, т. е. все её элементы, начиная с некоторого, по модулю меньше любого заранее взятого положительного числа.

В случае, если у числовой последовательности существует предел в виде вещественного числа , её называютсходящейся к этому числу. В противном случае, последовательность называют расходящейся. Если к тому же она неограниченна, то её предел полагают равным бесконечности.

Кроме того, если все элементы неограниченной последовательности, начиная с некоторого номера, имеют положительный знак, то говорят, что предел такой последовательности равен плюс бесконечности.

Если же элементы неограниченной последовательности, начиная с некоторого номера, имеют отрицательный знак, то говорят, что предел такой последовательности равен минус бесконечности.

Частичный предел последовательности — это предел одной из её подпоследовательностей.

Верхний предел последовательности — это наибольшая из её предельных точек.

Нижний предел последовательности — это наименьшая из её предельных точек.

Обозначения

Тот факт, что последовательность сходится к числуобозначается одним из следующих способов:

• 

• 

Свойства

Существуют определённые особенности для предела последовательностей вещественных чисел.^[2]

Можно дать альтернативные определения предела последовательности. Например, называть пределом число, в любой окрестности которого содержится бесконечно много элементов последовательности, в то время, как вне таких окрестностей содержится лишь конечное число элементов. Таким образом, пределом последовательности может быть только предельная точкамножества её элементов. Это определение согласуется с общим определением предела для топологических пространств.

Это определение обладает неустранимым недостатком: оно объясняет, что такое предел, но не даёт ни способа его вычисления, ни информации о его существовании. Всё это выводится из доказываемых ниже свойств предела.

Свойства

Арифметические свойства

• Операторвзятия предела числовой последовательности являетсялинейным, т. е. проявляет два свойства линейных отображений.

  • Аддитивность. Пределсуммычисловых последовательностей есть сумма их пределов, если каждый из них существует.

• Однородность.Константуможно выносить из-под знака предела.

• Предел произведения числовых последовательностей факторизуетсяна произведение пределов, если каждый из них существует.

• Предел отношения числовых последовательностей есть отношение их пределов, если эти пределы существуют и последовательность-делитель не является бесконечно малой.

Свойства сохранения порядка

• Если все элементы сходящейся последовательности, начиная с некоторого номера, не превышают некоторого числа, то и предел этой последовательности также не превышает этого числа.

• Если некоторое число не превышает все элементы сходящейся последовательности, начиная с некоторого номера, то оно также не превышает и предела этой последовательности.

• Если некоторое число строго превышает все элементы сходящейся последовательности, начиная с некоторого номера, то предел этой последовательности не превышает этого числа.

• Если все элементы сходящейся последовательности, начиная с некоторого номера, строго превышают некоторое число, то это число не превышает предела этой последовательности.

• Если, начиная с некоторого номера, все элементы одной сходящейся последовательности не превышают соответствующих элементов другой сходящейся последовательности, то и предел первой последовательности не превышает предела второй.

• Для числовых последовательностей справедлива теорема о двух милиционерах(принцип двустороннего ограничения).

Другие свойства

• Сходящаяся числовая последовательность имеет только один предел.

• Замкнутость. Если все элементы сходящейся числовой последовательности лежат на некоторомотрезке, то на этом же отрезке лежит и её предел.

• Предел последовательности из одного и того же числа равен этому числу.

• Замена или удаление конечного числа элементов в сходящейся числовой последовательности не влияет на её предел.

• У возрастающейограниченной сверху последовательности есть предел. То же верно для убывающей ограниченной снизу последовательности.

• Имеет место теорема Штольца.

• Если у последовательности 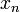существует предел, то последовательностьсредних арифметических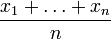имеет тот же предел (следствие из теоремы Штольца).

• Если у последовательности чисел 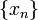существует предел, и если задана функция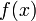, определенная для каждого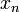и непрерывная в точке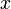, то

Примеры

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

Случай комплексных чисел

Комплексное числоназываетсяпределом последовательности , если для любого положительного числаможно указать такой номер, начиная с которого все элементыэтой последовательности удовлетворяют неравенствупри

Последовательность , имеющая предел, называется сходящейся к числу, что записывается в виде.

Примеры

Не у всякой ограниченной последовательности существует предел. Например, если взять в качестве пространства множество вещественных чиселсо стандартной топологией, а в качествепоследовательность, то у неё не будет предела (однако у неё можно найтиверхнийинижнийпределы,, то есть пределы её подпоследовательностей —частичные пределы).