7Основные теоремы о пределах. Арифметические операции над пределами.

Теорема 1. Если в точке существуют конечные пределы функцийи, то в этой точке существует и предел суммы, причем.

Теорема 2. Если в точке существуют пределы функцийи, то существует и предел произведения, причем.

Следствие 1. Постоянный множитель можно выносить за знак предела.

Действительно, .

Следствие 2..

Теорема 3. Если в точке существуют пределы функцийии при этом, то существует и предел частного, причем.

Теорема 4. Если в окрестности точки выполняется условиеи при этом функцииистремятся к одному и тому же пределу, то и функциятакже стремится к тому же пределу, т.е..

8.Первый замечательный предел

Доказательство

Рассмотрим односторонние пределы и и докажем, что они равны 1.

Пусть . Отложим этот угол на единичной окружности ().

Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке . ТочкаH — проекция точки K на ось OX.

Очевидно, что:

(1)

(где — площадь сектора)

(из :)

Подставляя в (1), получим:

Так как при :

Умножаем на :

Перейдём к пределу:

Найдём левый односторонний предел:

Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.

Следствия

• 

• 

• 

• 

Доказательства

9.Второй замечательный предел

или 

Доказательство второго замечательного предела:

Доказательство для натуральных значений

 Докажем вначале теорему для случая последовательности 

По формуле бинома Ньютона:

 

Полагая , получим:

Из данного равенства (1) следует, что с увеличением n число положительных слагаемых в правой части увеличивается. Кроме того, при увеличении n число убывает, поэтому величины возрастают. Поэтому последовательность — возрастающая, при этом

(2).

Покажем, что она ограничена. Заменим каждую скобку в правой части равенства на единицу, правая часть увеличится, получим неравенство

Усилим полученное неравенство, заменим 3,4,5, …, стоящие в знаменателях дробей, числом 2:

.

Сумму в скобке найдём по формуле суммы членов геометрической прогрессии:

.

Поэтому (3).

Итак, последовательность ограничена сверху, при этом выполняются неравенства (2) и (3):.

Следовательно, на основании теоремы Вейерштрасса (критерий сходимости последовательности) последовательность монотонно возрастает и ограниченна, значит имеет предел, обозначаемый буквойe. Т.е.

  Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что . Рассмотрим два случая:

1. Пусть . Каждое значение x заключено между двумя положительными целыми числами:, где— это целая часть x.

Отсюда следует: , поэтому

.

Если , то. Поэтому, согласно пределу, имеем:

.

По признаку (о пределе промежуточной функции) существования пределов .

2. Пусть . Сделаем подстановку, тогда

.

Из двух этих случаев вытекает, что для вещественного x.

Следствия

1. 

2. 

3. 

4. 

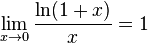
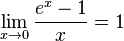
5. для ,

6. 

Доказательства следствий

1. 

2. 

3. 

4. 

5. 

6. 

10. Бесконечно малые функции. Свойства бесконечно малых.

Бесконечно малые функции Функция f (x) называется бесконечно малой функцией в точке х = х0, если  Аналогично определяются бесконечно малые функции при x → ∞, x → + ∞, x → – ∞, x → x0 – 0, x → x0 + 0. Можно дать равносильное определение бесконечно малой функции «на языке ε – δ: функция f (x) называется бесконечно малой в точке х = х0, если для любого как угодно малого ε > 0 существует δ = δ(ε) > 0, такое, что для всех х, удовлетворяющих неравенству 0 < | х – x0 | < δ, выполняется неравенство | f (x) | < ε. Или в символьном виде ( ε > 0) ( δ = δ(ε) > 0)( 0 < |х – х0| < δ ) : | f (x) | < ε.  Имеет место следующая теорема: функция f (x) в окрестности точки х0 отличается от своего предельного значения A на бесконечно малую функцию. Доказательство. Рассмотрим разность f (x) – А = α(х). Так как  то функция α(х) является бесконечно малой при x → х0.  Свойства бесконечно малых функций Опираясь на правила вычисления пределов, можно сформулировать свойства бесконечно малых: алгебраическая сумма и произведение конечного числа бесконечно малых функций при x → x0, а также произведение бесконечно малой функции на ограниченную функцию являются бесконечно малыми функциями при x → x0: 1.  Все сказанное о бесконечно малых функциях при x → x0 справедливо и для бесконечно малых функций при x → ∞, x → + ∞, x → – ∞, x → x0 – 0, x → x0 + 0.