4. Бесконечно малые и бесконечно большие последовательности. Их свойства. Бесконечно малые и бесконечно большие последовательности и их свойства.

Определение 27 (бесконечно малая последовательность). Бе- сконечно малая последовательность — последовательность, предел которой равен 0. То есть

lim_n ® Ґ x_n = 0

или более подробно с учетом определения предела " e>0 $ N: " n>N |x_n| < e Ю x_n.

Пример 20. Последовательность x_n = 1/n

является бесконечно малой последовательностью.

Определение 28 (бесконечно большая последовательность). x_n – бесконечно большая последовательность, если " c>0 $ N: " n>N |x_n|>c.

Пример 21. Последовательности n, 2ⁿ являются бесконечно большими.

Следует различать неограниченную и бесконечно большую последовательности. Всякая бесконечно большая последовательность является неограниченной, однако неограниченная не обязательно является бесконечно большой. Рассмотрим следующий пример.

Пример 22. Пусть x_n = 1,1/2,3,1/3,5,1/4,..., нетрудно заметить, что данная последовательность состоит из двух составляющих, а именно x_2k-1 = 2k-1, x_2k = 1/(k+1). Данная последовательность неограниченная, так как содержит неограниченную составляющую x_2k-1 = 2k-1, но не является бесконечно большой, так как содержит вторую часть x_2k = 1/(k+1).

Очевидно следующее утверждение.

Лемма 1. Если a_n — бесконечно малая последовательность, то 1/ a_n —бесконечно большая последовательность.

Пример 23. Пусть a_n = 1/n, которая является бесконечно малой, тогда последовательность b _n = 1/a _n = n будет бесконечно большой.

Теорема 5. Для того чтобы последовательность {x_n} имела предел, равный A необходимо и достаточно, чтобы ее члены имели вид

x_n = A+ a_n,

где lim _n ® Ґ a_n = 0.

Справедливы следующие свойства бесконечно малых последовательностей, которые легко получить из определения бесконечно малой последовательности.

Теорема 6. (свойства бесконечно малых последовательностей)

1. Сумма и разность двух бесконечно малых последовательностей является бесконечно малой последовательностью.

2. Произведение ограниченной последовательности на бесконечно малую последовательность является бесконечно малой последовательностью.

Следствие 1. Произведение конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью. Алгебраическая сумма конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью.

5. Свойства пределов последовательности, связанные с арифметическими операциями.

Сумма сходящихся последовательностей есть сходящаяся последовательность, предел которой равен сумме пределов исходных последовательностей.

Доказательство .

Пусть ,,,- бесконечно малая последовательность,,- бесконечно малая последовательность.

2. Если ,, то

3. Если ,, то

4. Если ,≠ 0, то=

6.Предел функции. Свойства предела функции в точке

1. Пусть функция определена в некоторой окрестности точкиа или в некоторых точках этой окрестности. Функция стремится к пределупри х, стремящемся к, если для каждого положительного числа , как бы мало оно ни было, можно указать такое положительное число, что для всехх, отличных от и удовлетворяющих неравенству, имеет место неравенство

 .

Если естьпредел функции f(x) при , то пишут:илиf (x) при .

2. Число b называется пределом функции в точке а, если для любой – окрестности точки b существует– окрестность точки а.

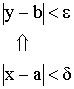
–предел функции при , равный b.

.Обозначение предела

Предел функции обозначается как или через символ предела:.  Всюду ниже предполагается, что пределы функцийсуществуют.

Предел суммы

Предел суммы двух функций равен сумме пределов этих функций:

Расширенное правило суммы

Предел постоянной величины

Предел постоянной величины равен самой постоянной величине:

Предел произведения функции на постоянную величину

Постоянный коэффициент можно выносить за знак предела:

Предел произведения

Предел произведения двух функций равен произведению пределов этих функций (при условии, что последние существуют):

Расширенное правило произведения

Предел частного

Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:

Предел степенной функции

где степень p - действительное число. В частности,

Если f ( x ) = x, то

Предел показательной функции

где основание a > 0. 

Предел логарифмической функции

где основание a > 0. 

Теорема "о двух милиционерах"

Предположим, что для всехx близких к a, за исключением, быть может, самой точкиx = a. Тогда, если

то

То есть функция f (x) остается "зажатой" между двумя другими функциями, стремящимися к одному и тому же пределу L.