15. Собственные векторы и собственные значения матрицы.

Собственным векторомлинейного преобразованияназывается такой ненулевойвектор, что для некоторого

Собственным значением линейного преобразования называется такое число, для которого существует собственный вектор, то есть уравнениеимеет ненулевое решение.

Упрощённо говоря, собственный вектор — любой ненулевой вектор x, который отображается оператором в коллинеарный , а соответствующий скалярназываетсясобственным значением оператора.

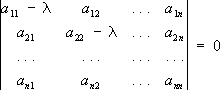 Собственные значения матрицы  (i, k = 1, 2,..., n) называют Собственные значениясоответствующего ей линейного преобразования п-мерного комплексного пространства. Их можно определить также как корни определителя матрицы А — lЕ (где Е — единичная матрица), т. е. корни уравнения   , (*)   называемого характеристическим уравнением матрицы

16.Ортонормированные системы векторов и их свойства

Если длина вектора равна единице, он называется нормированным вектором:(x,x)= 1,|x| = 1.

Если все векторы системы векторов нормированы, то система векторов называется нормированной системой.

Если векторы системы векторов e₁,e₂,..., e_nпопарно ортогональны и нормированы, то система векторов называетсяортонормированной системой:(e_i, e_j) = 0, если i ≠ j ,(e_i, e_i) = 1.

Если e₁,e₂,..., e_n — ортонормированная система иx=x₁e₁+x₂e₂+ ... +x_ne_n — разложение вектораxпо этой системе, то x_i =(x, e_i).

17 Линейные операторы. Матрица линейного оператора.

Пусть заданы линейные пространства X и Y. Правило, по которому каждому элементу x e X ставится в соответствие единственный элемент y e Y , называется оператором, действующим в линейных пространствах X , Y. Результат действия оператора A на элемент x обозначают y = A x или y = A(x). Если элементы x и y связаны соотношением y = A x, то y называют образом элемента x; элемент x прообразом элемента y.

Множество элементов линейного пространства X, для которых определено действие оператора A, называют областью определения оператора и обозначают D(A).

Множество элементов линейного пространства Y, которые являются образами элементов из области определения оператора A, называют образом оператора и обозначают Im(A). Если y = A x , то x e D(A), y e Im(A) .

Оператор A, действующий в линейных пространствах X , Y называется линейным оператором, если

A(u+v)=A(u)+A(v) и A(au)=aA(u) и для любых u,v e X и для любого числа a.

Если пространства X и Y совпадают, то говорят, что оператор действует в пространстве X. 2) Рассмотрим линейный оператор A, действующий в конечномерном линейном пространстве X, dim(x)=n и пусть e1, e2, ..., en - базис в X. Обозначим через A e1 = (a11,...,an1), ... , A en = (a1n,...,ann) образы базисных векторов e1, e2, ..., en .

Матрица столбцами которой являются координаты образов базисных векторов, называется матрицей линейного оператора в заданном базисе.

Доказано, что каждому линейному оператору, действующему в n-мерном линейном пространстве, отвечает единственная квадратная матрица порядка n; и обратно каждая квадратная матрица порядка n задает единственный линейный оператор, действующий в этом пространстве. Замечание 1. Если оператор А нулевой, то все элементы матрицы А этого оператора равны нулю в любом базисе, т.е. А — нулевая матрица.

Замечание 2. Если оператор А единичный, т. е. А = I, то матрица этого оператора будет единичной в любом базисе. Иными словами, в этом случае А = Е, где Е — единичная матрица. В дальнейшем единичную матрицу мы будем обозначать также символом I.