2.2 Оценка влияния факторов внешней и внутренней среды на организацию

Оценка влияния факторов внешней и внутренней среды организации мы будем проводить при помощи экспертного метода и регрессионного анализа. Регрессионный анализ позволит нам выявить тесноту связи между двумя факторами, которые влияют на внутреннюю среду организации.

В свою очередь метод экспертных оценок позволит выявить факторы внешней и внутренней среды организации, которые влияют на систему управления предприятием в целом. Воспользовавшись регрессионным анализом, с помощью линейного метода сначала определим зависимости вида y=a+bx между годовым объемом продаж и годовыми расходами на рекламу «Информационно – риэлтерской службы Экспресс-Недвижимость», за предшествующие годы были собраны следующие данные:

	Объем продаж (млн.руб) x	Расходы на рекламу (тыс.руб) y	yx	xˆ2	yˆ2
	65	24	1560	4225	576
	60	21	1260	3600	441
	58	18	1044	3364	324
	47	13	611	2209	169
	40	10	400	1600	100
Сумма	270	86	4875	14998	1610
Сред.зн.	54	17.2	975	2999.6	322

∑y=na+b(∑x)

∑xy=a(∑x)+b(∑x²)

В нашем случае n=5 – число наблюдений и:

∑x=270, ∑y=86, ∑xy=4875, ∑x²=14998

Подставим эти значения в вышеуказанные уравнения:

86=5a+270b

4875=270a+14998b

решив эту систему относительно a и b получим a=-10.5 и b=0.55. таким образом ожидаемые продажи будут составлять -10.5 плюс 0.55 умножить на рекламный бюджет.

y=-10.5+0.55x

С помощью формулы вычислим коэффициент корреляции:

R=

Данный коэффициент равняется -0.09. Это говорит о том, что годовой объем продаж будет сильно зависеть от годового расхода на рекламу.

Экспертный анализ

Для экспертного анализа мы отобрали 5 экспертов, для опроса экспертов была разработана специальная анкета (Приложение 1). Эксперты должны были пройти анкету, и расставить баллы от 1 до 10 под ответами, в зависимости от важности. Ниже представлены полученные в результате опроса данные:

Баллы полученные при опросе

Факторы	Эксперты
	1-ый	2-ой	3-ий	4-ый	5-ый
1. Необходимо усовершенствовать услуги	6	5	3	2	4
2. Да, ассортимент услуг стоить стоит улучшить, т.к. у предприятия стабильное финансовое положение	3	4	1	2	6
3. Конкурентоспособность можно улучшить за счет рекламной политики	5	6	3	4	1
4. Внедрение новой услуги может привести к популярности фирмы, появятся новые клиенты	2	1	4	6	5
5. Выход на новый рынок приведет к популярности фирмы, сможет укрепить финансовое состояние предприятия	2	1	6	5	3
6. Необходимы квалифицированные работники, с постоянным повышением квалификации	1	5	4	2	3

По данным выше представленной таблицы было опрошено 5 экспертов по 6 признаком. Рассмотрим построение матрицы по каждому из методов сбора данных. При ранжирование, здесь в качестве исходной информации используется матрица R.

R = .

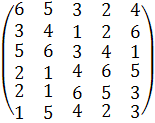Построим матрицу преобразований рангов каждый элемент, которой определяется по формуле = n-

=.

= =15

Строится матрица нормальных весов : =() при чём каждый элемент =

X==,

Классической мерой близости является квадрат отклонения, поэтому наиболее распространенный метод построения центроида есть нахождение вектора столбца W такого, что = * , найдём центроид:

W= =

После чего строим

=

Уточнить вектор компетентности и в результате больший вес должен получить тот эксперт, который дал большую оценку фактору, получившему большое групповое предпочтение.Для этого построим матрицу B=*X, где - транспонированная:

B= * =

= .

После этого находим вектор «невзвешанных» коэффициентов для экспертов:

= B*= *

= .

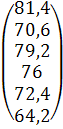После нормирования получаем веса комплектности после первой итерации:

= =

В данном эксперименте проводилось 4 итерации. Таким образом вторую итерацию будем находит аналогично:

= B*= * =

=

==

Ниже представлены данные 4 итераций:

= B*= * =

=

==

Далее проводим четвёртую итерацию:

= B*= * =

=

==

На следующем этапе мы пытаемся оценить, можно ли доверять полученным данным.Для этого найдём коэффициент канкордации Кенделла. Сначала найдём сумму элементов в каждой строке матрицы R:

= =.

Далее вычисляем среднее значение по формуле:

= = = 17,5

Определим сумму квадратов отклонений значений в строке матрицы R от , то есть S по формуле: S= =

++++=6,25+2,25+2,25+0,25+0,25+6,25=17,5

По ниже приведённой формуле находим коэффициент Кенделля:

W= = = 0,04

W=

Проверим полученное значение W. Для этого найдём:

=m (n-1)=*W= 5(6-1)* 0,04= 1

Далее по таблице квантилей распределения Пирсона по уровню значимости K= n-1= 6-1 =5 и надёжности =0,05 находим число. Оно равняется 0,25. , коэффициент W значим, все вычисления верны.