Доверительное оценивание по вариационному ряду.

Пусть задана выборка  некоторой случайной величины  Построим вариационный ряд выборки 

Очевидно, что вероятность попасть в любой из  - го интервалов значений случайной ведичины  одинакова и равна Тогда вероятность того, что случайная величина  приняла значение из интервала  где  будет равна:

Вопрос: чему должен быть равен размер выборки  чтобы вероятность попасть в интервал  составила 95%.

Подставляя значение для доверительной вероятности в формулу выше, получим:

откуда 

Таким образом, при достаточном для заданной доверительной вероятности числе измерений случайной величины  по набору еепорядковых статистик может быть оценен диапазон принимаемых ею значений.

Пример 2. Доверительный интервал для медианы.

Таблица 1

Пусть задана выборка  некоторой случайной величины 

• При 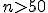 доверительный интервал для медианы 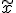 определяется порядковыми статистиками

где

 при 

 при 

 при 

• Для значений 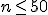 номера порядковых статистик, заключающих в себе медиану, пр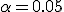и  и  приведены в таблице 1, взятой из [3].

Пример 3. Доверительный интервал для математического ожидания.

Пусть задана выборка  некоторой случайной величины , арактеристики которой (дисперсия D и математическое ожидание M) неизвестны. Эти параметры оценим так:

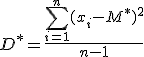 - несмещенная оценка дисперсии.

Величину  называют оценкой среднего квадратического отклонения. Воспользуемся тем, что величина  представляет собой сумму  независимых случайных величин, и, согласно центральной предельной теореме, при достаточно большом  ее закон близок к нормальному. Поэтому будем считать, что величина  распределена по нормальному закону. Характеристики этого закона - математическое ожидание и дисперсия - равны соответственно M (настоящее МО случайной величины ) и .

Найдем такую величину , для которой . Перепишем это в эквивалентном виде  и скажем, что случайная величина перед знаком неравенства есть модуль от стандартной нормальной. Получаем, что , и . В случае неизвестной дисперсии ее можно заменить на оценку .

Квантили стандартного нормального распределения:

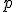
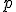
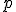
	Квантиль порядка		Квантиль порядка
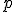
0.01	-2.326348	0.60	0.253347
0.025	-1.959964	0.70	0.524401
0.05	-1.644854	0.80	0.841621
0.10	-1.281552	0.90	1.281552
0.30	-0.524401	0.95	1.644854
0.40	-0.253347	0.975	1.959964
0.50	0	0.99	2.326348

Например, выбирая , получаем коэффициент 

Окончательно: с вероятностью  можно сказать, что 

31. Доверительное оценивание параметров нормального распределения.

32. Оценка вероятности появления события по частоте в n независимых опытах.

При проведении экспериментов часто приходится оценивать неизвестную вероятность события P по его частоте  в N независимых экспериментах. Частота некоторого события в N независимых экспериментах есть не что иное, как среднее арифметическое наблюдаемых значений величины Х, которая в каждом отдельном опыте принимает значение 1 (если событие совершилось), или значение 0 (если событие не произошло):

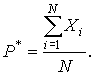
В [1] показано, что математическое ожидание величины Х равно Р, а ее дисперсия равна Р(1-P). Математическое ожидание выборочного среднего равно Р:

т.е. оценка  является несмещенной. Дисперсия величины  равна:

Специфика этой задачи в том, что Х в данном случае - дискретная случайная величина только с двумя возможными значениями: 0 и 1. Сделаем ограничение практически всегда выполняемым - число экспериментов достаточно велико, так что выполняются условия:

N(1-P) > 4, NP > 4.

Если эти условия выполнены, то частоту  можно считать распределенной по гауссовскому закону. Тогда параметры этого закона:

В [1] приведена методика оценки доверительного интервала, которую мы приведем далее. Границы интервала, в котором заключено истинное значение вероятности события, определяются следующим образом:

, .

Здесь  - конкретная оценка вероятности (частоты события), а t находится, исходя из заданной доверительной вероятности :

.

33. Основы теории проверки статистических гипотез. Понятие статистического критерия, критической области.

34. Критерий согласия Хи-квадрат о виде распределения.

Критерий согласия Пирсона χ²  – один из основных, который можно представить как сумму отношений квадратов расхождений между теоретическими (f_Т) и эмпирическими (f) частотами к теоретическим частотам:

  

• k–число групп, на которые разбито эмпирическое распределение,  

• f_i–наблюдаемая частота признака в i-й группе,

• f_T–теоретическая частота.

35. Критерий согласия Романовского.

Критерий Романовского с основан на использовании критерия Пирсона,  т.е.  уже найденных значений , и числа степеней свободы df:

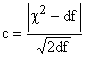
Он удобен при отсутствии таблиц для . Если с<3, то расхождения распределений случайны, если же с>3, то не случайны и теоретическое распределение не может служить моделью для изучаемого эмпирического распределения.