19. Вероятность попадание случайной точки в заданную область (в том числе прямоугольную).

Вероятность попадания случайной точки в заданную область выражаются наиболее просто в том случае, когда эта область представляет собой прямоугольник со сторонами, параллельными координатным осям.

Выразим через функцию распределения системы вероятность попадания случайной точки  в прямоугольник , ограниченный абсциссами  и  и ординатами  и  (рис. 8.2.5).

При этом следует условиться, куда мы будем относить границы прямоугольника. Аналогично тому, как мы делали для одной случайной величины, условимся включать в прямоугольник  его нижнюю и левую границы и не включать верхнюю и правую. Тогда событие  будет равносильно произведению двух событий:  и . Выразим вероятность этого события через функцию распределения системы. Для этого рассмотрим на плоскости  четыре бесконечных квадранта с вершинами в точках ; ;  и  (рис. 8.2.6).

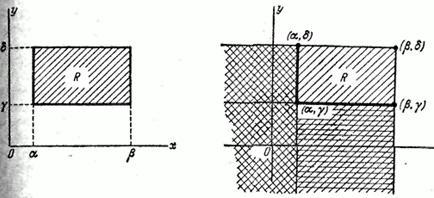
Рис. 8.2.5.                                             Рис. 8.2.6

Очевидно, вероятность попадания в прямоугольник  равна вероятности попадания в квадрант  минус вероятность попадания в квадрант  минус вероятность попадания в квадрант  плюс вероятность попадания в квадрант  (так как мы дважды вычли вероятность попадании в этот квадрант). Отсюда получаем формулу, выражающую вероятность попадания в прямоугольник через функцию распределения системы:

.       

20. Независимость нескольких случайных величин. Связь с коэффициентом корреляции.

Случайные величины  называют независимыми (в совокупности), если для любого набораборелевских множеств , ...,  имеет место равенство:

Коэффициент корреляции - это сила и направление связи между независимой и зависимой переменными. Значения r находятся в диапазоне между - 1.0 и + 1.0. Когда r имеет положительное значение, связь между х и у является положительной, а когда значение r отрицательно, связь также отрицательна. Коэффициент корреляции, близкий к нулевому значению, свидетельствует о том, что между х и у связи не существует.

21. Ковариация, коэффициент корреляции, их свойства. Условные законы распределения.

Ковариация являетcя совместным центральным моментом второго порядка.[6] Ковариация определяется как математическое ожидание произведения отклонений случайных величин

Так как и — независимые случайные величины, то и их отклонения и также независимы. Пользуясь тем, что математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий сомножителей, а математическое ожидание отклонения равно нулю, имеем

Свойства ковариации:

Ковариация двух независимых случайных величин и равна нулю^[

Абсолютная величина ковариации двух случайных величин и не превышает среднего геометрического их дисперсий:

Условные законы распределения

Пусть известна плотность распределения системы двух случайных величин. Используя свойства функций распределения, можно вывести формулы для нахождения плотности распределения одной величины, входящей в систему:

(5.3)

Перейдем теперь к решению обратной задачи: по известным законам распределения отдельных величин, входящих в систему, найти закон распределения системы. Легко увидеть, что в общем случае эта задача неразрешима. Действительно, с одной стороны, законы распределения отдельных случайных величин, входящих в систему, характеризуют каждую из случайных величин в отдельности, но ничего не говорят о том, как они взаимосвязаны. С другой стороны, искомый закон распределения системы должен содержать все сведения о случайных величинах системы, в том числе и о характере связей между ними.

Таким образом, если случайные величины  взаимозависимы, то закон распределения системы не может быть выражен через законы распределения отдельных случайных величин, входящих в систему. Это приводит к необходимости введения условных законов распределения.

Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина, входящая в систему, приняла определенное значение, называется условным законом распределения.

Условный закон распределения можно задавать как функцией распределения, так и плотностью распределения. Условная функция распределения обозначается , условная плотность распределения —  (мы записали условные законы распределения случайной величины  при условии, что другая случайная величина  приняла определенное значение).

Плотностью распределения для случайной величины  при условии, что случайная величина  приняла определенное значение (условной плотностью распределения), назовем величину

Аналогично плотностью распределения для случайной величины  при условии, что случайная величина  приняла определенное значение, назовем величину

. Отсюда получаем .

или с учетом формул (5.3)

Условная плотность распределения обладает всеми свойствами безусловной плотности распределения. В частности,

22. Числовые характеристики случайных величин и их свойства.

23. Неравенство Чебышева. Закон больших чисел в форме Чебышева.

Одно из основных утверждений закона больших чисел состоит в том, что значение среднеарифметического 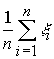случайных величин с равными математическими ожиданиями  при большом n (при некоторых широких условиях) оказывается приближенно равным a:

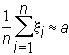
уточним: будем писать

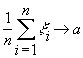 при  ,

если для любого e >0 и достаточно больших n соотношение

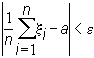             (2)

выполняется с вероятностью, стремящейся к 1 с ростом n; запишем это так:

 при  .

это одно из утверждений закона больших чисел. Заметим, что, как и теорема Бернулли, оно не означает, что соотношение (2) достоверно; однако, если n достаточно велико, то вероятность его выполнения близка к 1, например, 0.98 или 0.999, что означает практически достоверно. Приведем полную формулировку одной из теорем закона больших чисел в форме Чебышева,