24. Характеристическая функция, ее свойства.

Свойства характеристических функций[править | править исходный текст]

• Характеристическая функция однозначно определяет распределение. Пусть  суть две случайные величины, и 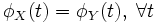. Тогда . В частности, если обе величины абсолютно непрерывны, то совпадение характеристических функций влечёт совпадение плотностей. Если обе случайные величины дискретны, то совпадение характеристических функций влечёт совпадение функций вероятности.

• Характеристическая функция всегда ограничена:

.

• Характеристическая функция в нуле равна единице:

.

• Характеристическая функция всегда непрерывна: .

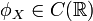• Характеристическая функция как функция случайной величины однородна:

.

• Характеристическая функция суммы независимых случайных величин равна произведению их характеристических функций. Пусть 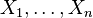 суть независимые случайные величины. Обозначим . Тогда

.

• Для всех вещественных  верно равенство , где  означает комплексно сопряжённую с  функцию^[1].

• Теорема обращения (Леви). Пусть  - функция распределения, а  - её характеристическая функция. Если и  - точки непрерывности , то

25. Основные задачи математической статистики. Эмпирическая функция распределения. Гистограмма, полигон частот. Выборочные характеристики.

26. Задачи теории оценивания. Точечное оценивание. Свойства точечных оценок.

 Оценкапараметра — соответствующая числовая характеристика, рассчитанная по выборке. Когда оценка определяется одним числом, она называется точечной оценкой.

Свойства точечных оценок[

Оценка  называется несмещённой, если её математическое ожидание равно оцениваемому параметру генеральной совокупности:

,

где  обозначает математическое ожидание в предположении, что  — истинное значение параметра (распределения выборки ).

• Оценка  называется эффективной, если она обладает минимальной дисперсией среди всех возможных несмещенных точечных оценок.

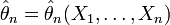• Оценка  называется состоятельной, если она по вероятности с увеличением объема выборки n стремится к параметру генеральной совокупности: ,

 по вероятности при .

• Оценка  называется сильно состоятельной, если ,

 почти наверное при .

Надо отметить, что проверить на опыте сходимость «почти наверное» не представляется возможным, поэтому с точки зрения прикладной статистики имеет смысл говорить только о сходимости по вероятности.

27. Оценки математического ожидания и дисперсии, их свойства.

 Арифметическая средняя , вычисленная по n независимым наблюдениям над случайной величиной x, которая имеет математическое ожидание Mx = m, является несмещенной оценкой этого параметра.

Арифметическая средняя , вычисленная по n независимым наблюдениям над случайной величиной x, которая  имеет Mx = m  и  ,  является состоятельной оценкой этого параметра.

Если случайная выборка состоит из n независимых наблюдений над случайной величиной  x с

 Mx = m  и  Dx = , то выборочная дисперсия

                                                                                         (23.3)

не является несмещенной оценкой Dx  - генеральной дисперсии.

28. Метод моментов.

29. Метод максимального правдоподобия.

30. Интервальное (доверительное) оценивание.