5. Варианты заданий

На рис. 7 показана транспортная сеть, соединяющая населенные пункты, и расстояния между ними. Найдите кратчайшее остовное дерево для своего варианта.

Варианты	Города
1	Чебоксары – Мариинский Посад – Цивильск – Урмары – Янтиково – Канаш – Калинино
2	Чебоксары – Новочебоксарск – Цивильск – Урмары – Янтиково – Канаш – Калинино
3	Чебоксары – Новочебоксарск – Тюрлема – Урмары – Янтиково – Канаш – Калинино
4	Чебоксары – Мариинский Посад – Тюрлема – Урмары – Янтиково – Канаш – Калинино
5	Чебоксары – Красноармейское – Цивильск – Урмары – Янтиково – Канаш – Калинино
6	Чебоксары – Красноармейское – Калинино – Аликово – Красные Четаи – Ядрин – Моргауши
7	Чебоксары – Калинино – Шумерля – Красные Четаи – Ядрин – Моргауши
8	Канаш – Комсомольское – Яльчики – Батырево – Ибреси – Вурнары – Калинино
9	Канаш – Комсомольское – Яльчики – Алатырь – Ибреси – Вурнары – Калинино
10	Новочебоксарск – Цивильск – Канаш – Ибреси – Вурнары – Калинино – Чебоксары
11	Канаш – Ибреси – Батырево – Алатырь – Порецкое – Шумерля – Калинино
12	Алатырь – Порецкое – Шумерля – Калинино – Канаш – Ибреси – Батырево

Рис. 7. Транспортная сеть Чувашии

Лабораторная работа № 19

ЗАДАЧА ПОИСКА КРАТЧАЙШЕГО ПУТИ

1. ЦЕЛЬ РАБОТЫ

Сформировать у студентов знания, умения и навыки поиска кратчайшего пути в математическом пакете MathСad.

2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Изучите теоретическую часть. Выполните задание, соответствующее номеру Вашего варианта, и продемонстрируйте его преподавателю.

2. Оформите отчет по лабораторной работе, который должен содержать:

• титульный лист (Рис. 2);

• исходные данные варианта;

• последовательность действий для решения задачи;

• результаты решения задачи.

3. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

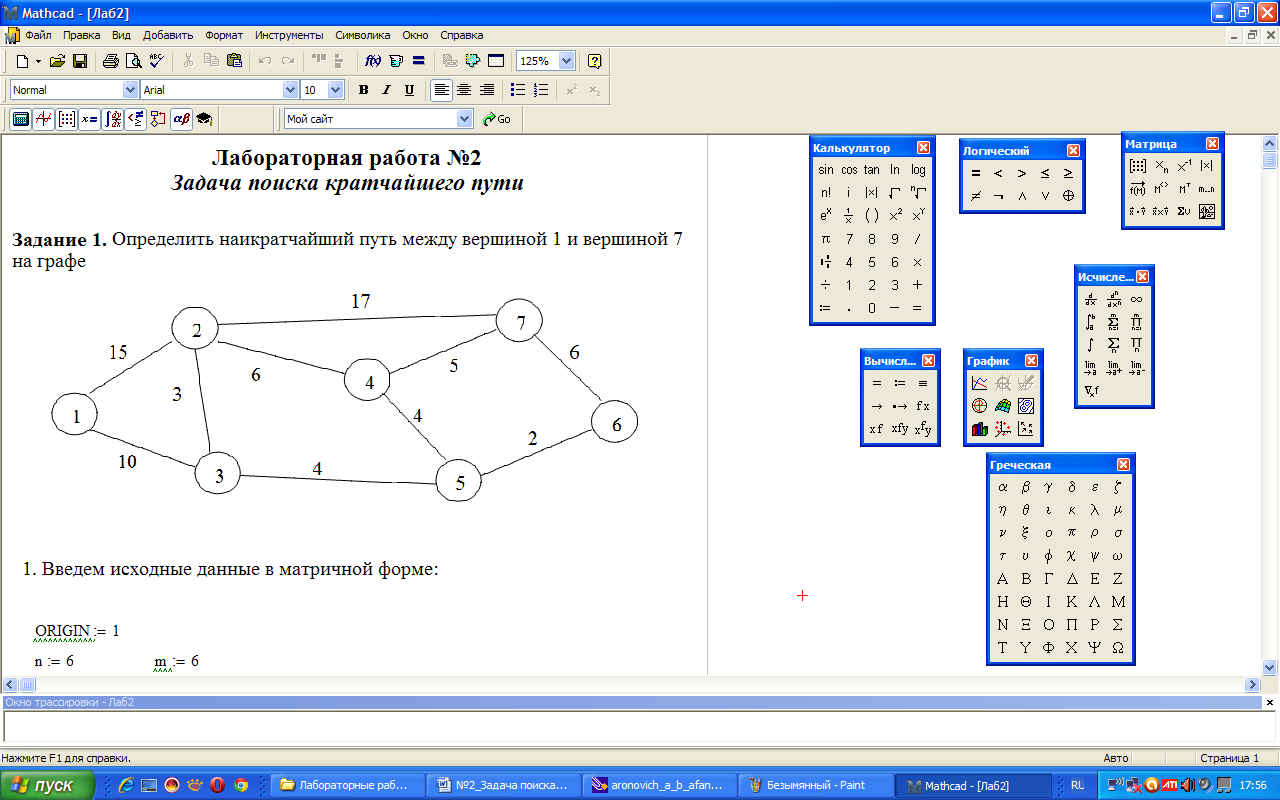
Рассмотрим задачу: определить наикратчайший путь между вершиной 1 и вершиной 7 на графе, представленном на рис. 8.

Рис. 8. Исходные данные задачи

Для решения задачи в MathCad представим ее как транспортную задачу с промежуточными пунктами. Будем считать, что транспортные расходы при перевозке одной единицы груза равны (в условных единицах) расстояниям между вершинами. Одна единица груза отправляется из вершины 1 (исходный пункт) и должна прибыть в вершину 7 (пункт назначения). Вершины 2, 3, 4, 5, 6 рассматриваются как промежуточные пункты, которые являются одновременно и исходными пунктами и пунктами назначения.

Требуется определить такую последовательность вершин, по которым должна перемещаться единица груза, отправленная из вершины 1, при которой стоимость транспортных расходов будет минимальна и груз попадет в вершину 7.

4. Образец выполнения

Пример.

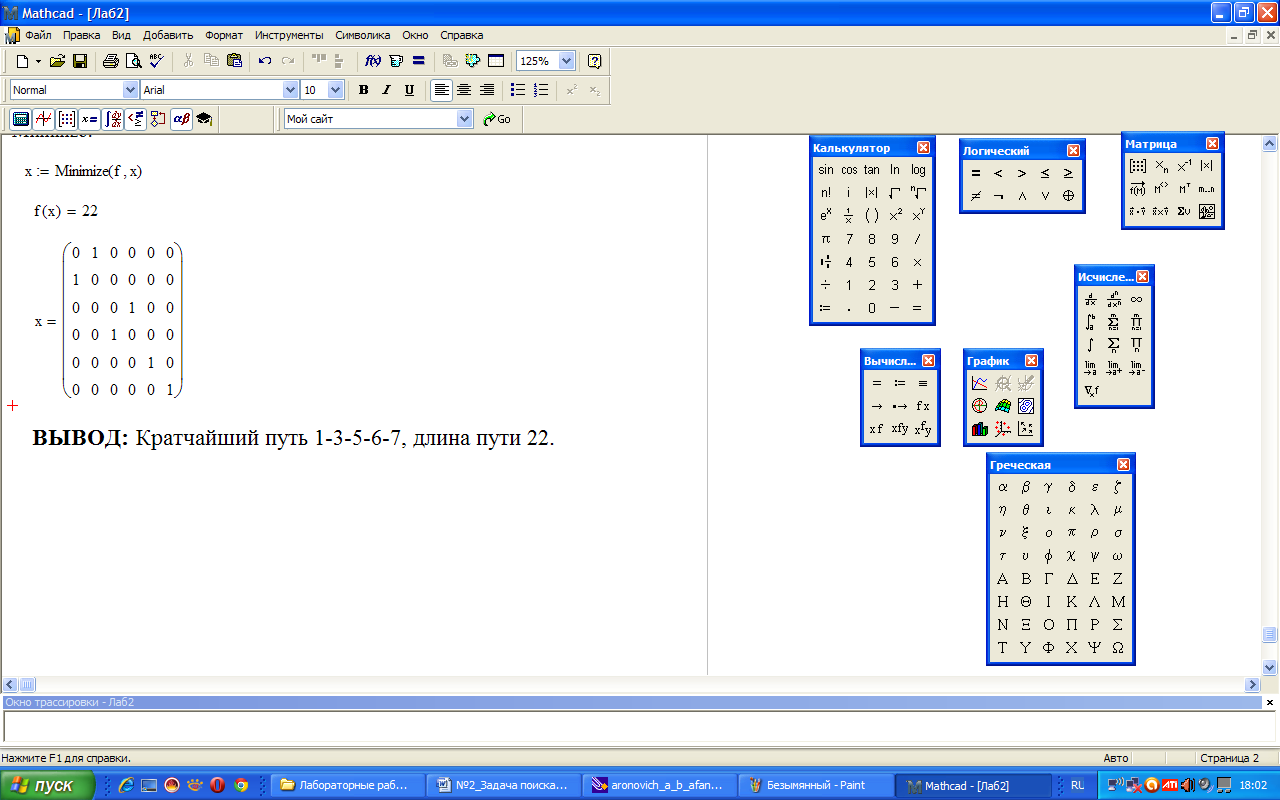
5. Варианты заданий

На рис. 7 показана транспортная сеть, соединяющая 24 населенных пунктов, и расстояния между ними. Найдите кратчайшие маршруты между следующими населенными пунктами:

Вариант	Маршрут
1	Шемурша – Ядрин
2	Шемурша – Аликово
3	Красные Четаи – Яльчики
4	Порецкое – Козловка
5	Шумерля – Козловка
6	Моргауши – Батырево
7	Чебоксары – Алатырь
8	Ибреси – Ядрин
9	Шемурша – Красноармейское
10	Урмары – Порецкое
11	Моргауши –Ибреси
12	Мариинский Посад – Шемурша