4. Образец выполнения

Пример 1.

Пример 2. Предположим дана функция и нужно найти первообразную к нейF(x) так, что F(1) = 2, и построить график F(x) на промежутке [1; 8].

Вводим ЗадаёмПроверяем

_{Строим график}

5. ВАРИАНТЫ ЗАДАНИЙ

Вариант 1

Задание 1. Найдите определённые интегралы

, ,.

Для первого и второго интегралов найдите точные символьные выражения, используя знак . Третий («неберущийся») интеграл найдите с точностью до 0.0000001. Для вывода на экран всех нужных знаков числа используйте кнопкиФормат – Результат на верхней панели.

Задание 2. Найдите первообразную F(x) для функции , такую, чтоF(1) = 2 . Постройте график функции F(x) на промежутке .

Вариант 2

Задание 1. Найдите определённые интегралы

, ,.

Для первого и второго интегралов найдите точные символьные выражения, используя знак . Третий («неберущийся») интеграл найдите с точностью до 0.0000001. Для вывода на экран всех нужных знаков числа используйте кнопкиФормат – Результат на верхней панели.

Задание 2. Найдите первообразную F(x) для функции , такую, чтоF(0) = 0 . Постройте график функции F(x) на промежутке .

Вариант 3

Задание 1. Найдите определённые интегралы

, ,.

Для первого и второго интегралов найдите точные символьные выражения, используя знак . Третий («неберущийся») интеграл найдите с точностью до 0.0000001. Для вывода на экран всех нужных знаков числа используйте кнопкиФормат – Результат на верхней панели.

Задание 2. Найдите первообразную F(x) для функции , такую, чтоF(1) = 1 . Постройте график функции F(x) на промежутке .

Вариант 4

Задание 1. Найдите определённые интегралы

, ,.

Для первого и второго интегралов найдите точные символьные выражения, используя знак . Третий («неберущийся») интеграл найдите с точностью до 0.0000001. Для вывода на экран всех нужных знаков числа используйте кнопкиФормат – Результат на верхней панели.

Задание 2. Найдите первообразную F(x) для функции , такую, чтоF(0) = 1 . Постройте график функции F(x) на промежутке .

Вариант 5

Задание 1. Найдите определённые интегралы

, ,.

Для первого и второго интегралов найдите точные символьные выражения, используя знак . Третий («неберущийся») интеграл найдите с точностью до 0.0000001. Для вывода на экран всех нужных знаков числа используйте кнопкиФормат – Результат на верхней панели.

Задание 2. Найдите первообразную F(x) для функции , такую, чтоF(0) = 0 . Постройте график функции F(x) на промежутке .

Вариант 6

Задание 1. Найдите определённые интегралы

, ,.

Для первого и второго интегралов найдите точные символьные выражения, используя знак . Третий («неберущийся») интеграл найдите с точностью до 0.0000001. Для вывода на экран всех нужных знаков числа используйте кнопкиФормат – Результат на верхней панели.

Задание 2. Найдите первообразную F(x) для функции , такую, чтоF(1) = 0 . Постройте график функции F(x) на промежутке .

Вариант 7

Задание 1. Найдите определённые интегралы

, ,.

Для первого и второго интегралов найдите точные символьные выражения, используя знак . Третий («неберущийся») интеграл найдите с точностью до 0.0000001. Для вывода на экран всех нужных знаков числа используйте кнопкиФормат – Результат на верхней панели.

Задание 2. Найдите первообразную F(x) для функции , такую, чтоF(0) = 0 . Постройте график функции F(x) на промежутке .

Вариант 8

Задание 1. Найдите определённые интегралы

, ,.

Для первого и второго интегралов найдите точные символьные выражения, используя знак . Третий («неберущийся») интеграл найдите с точностью до 0.0000001. Для вывода на экран всех нужных знаков числа используйте кнопкиФормат – Результат на верхней панели.

Задание 2. Найдите первообразную F(x) для функции , такую, чтоF(0) = 1 . Постройте график функции F(x) на промежутке .

Вариант 9

Задание 1. Найдите определённые интегралы

, ,.

Для первого и второго интегралов найдите точные символьные выражения, используя знак . Третий («неберущийся») интеграл найдите с точностью до 0.0000001. Для вывода на экран всех нужных знаков числа используйте кнопкиФормат – Результат на верхней панели.

Задание 2. Найдите первообразную F(x) для функции , такую, чтоF(0) = 1 . Постройте график функции F(x) на промежутке .

Вариант 10

Задание 1. Найдите определённые интегралы

, ,.

Для первого и второго интегралов найдите точные символьные выражения, используя знак . Третий («неберущийся») интеграл найдите с точностью до 0.0000001. Для вывода на экран всех нужных знаков числа используйте кнопкиФормат – Результат на верхней панели.

Задание 2. Найдите первообразную F(x) для функции , такую, чтоF(0) = 1 . Постройте график функции F(x) на промежутке .

Вариант 11

Задание 1. Найдите определённые интегралы

, ,.

Для первого и второго интегралов найдите точные символьные выражения, используя знак . Третий («неберущийся») интеграл найдите с точностью до 0.0000001. Для вывода на экран всех нужных знаков числа используйте кнопкиФормат – Результат на верхней панели.

Задание 2. Найдите первообразную F(x) для функции , такую, чтоF(2) = 1 . Постройте график функции F(x) на промежутке .

Вариант 12

Задание 1. Найдите определённые интегралы

, ,.

Для первого и второго интегралов найдите точные символьные выражения, используя знак . Третий («неберущийся») интеграл найдите с точностью до 0.0000001. Для вывода на экран всех нужных знаков числа используйте кнопкиФормат – Результат на верхней панели.

Задание 2. Найдите первообразную F(x) для функции f(x) = , такую, чтоF(2) = 1 . Постройте график функции F(x) на промежутке .

ЛАБОРАТОРНАЯ РАБОТА № 12

ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА

1. ЦЕЛЬ РАБОТЫ

Исследовать геометрические приложения определенного интеграла в математическом пакете MathСad.

2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1. Изучите теоретическую часть. Выполните задание, соответствующее номеру Вашего варианта, и продемонстрируйте его преподавателю.

2. Оформите отчет по лабораторной работе, который должен содержать:

• титульный лист (Рис. 2);

• исходные данные варианта;

• последовательность действий для решения задачи;

• результаты решения задачи.

3. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

1. Площадь плоской фигуры

а) Площадь криволинейной трапеции, ограниченной кривой , прямымиии отрезком, вычисляется по формуле.

б) Площадь фигуры, ограниченной кривыми ии прямымии, находится по формуле.

в) Если кривая задана параметрическими уравнениями и, то площадь криволинейной трапеции, ограниченной этой кривой, прямымиии отрезком, выражается формулой, гдеt₁ и t₂ определяются из уравнений и.

г) Площадь криволинейного сектора находится по формуле .

2. Длина дуги плоской кривой

а) Если кривая на отрезке– гладкая, то есть– непрерывна, то длина соответствующей дуги этой кривой находится по формуле

б) Если уравнение кривой задано параметрически, то длина дуги кривой, соответствующая монотонному изменению параметра t от t₁ до t₂, вычисляется по формуле

в) Если кривая задана в полярных координатах, то

3. Объем тела

а) Если площадь сечения тела плоскостью, перпендикулярной оси Ох может быть выражена как функция от x, то есть в виде , то объем части тела, заключенной между перпендикулярными осиОх плоскостями и, находится по формуле:

б) Если криволинейная трапеция, ограниченная кривой и прямыми,и, вращается вокруг осиОх, то объем тела вращения вычисляется по формуле:

в) Если фигура, ограниченная кривыми ии прямымии, вращается вокруг осиОх, то объем тела вращения:

4. Площадь поверхности тела вращения

а) Если дуга гладкой кривой вращается вокруг осиОх, то площадь поверхности вращения вычисляется по формуле:

б) Если кривая задана параметрическими уравнениями и, то

4. ОБРАЗЕЦ ВЫПОЛНЕНИЯ

Пример 1. Найдите S фигуры, ограниченной линиями и

Решение:

Для нахождения площади фигуры зададим две функции:

Построим графики этих функций

Так как непосредственно по графикам функций невозможно определить точные координаты точек пересечения, найдем пределы интегрирования как корни уравнения . Для этого перенесем все в левую часть, приравняв, таким образом, к нулю, и воспользуемся встроенной вMathcad функцией «solve»:

Или можно использовать логическое равенство из панели инструментов «Логический», тогда запись будет иметь вид:

Далее составим определенный интеграл и вычислим площадь фигуры:

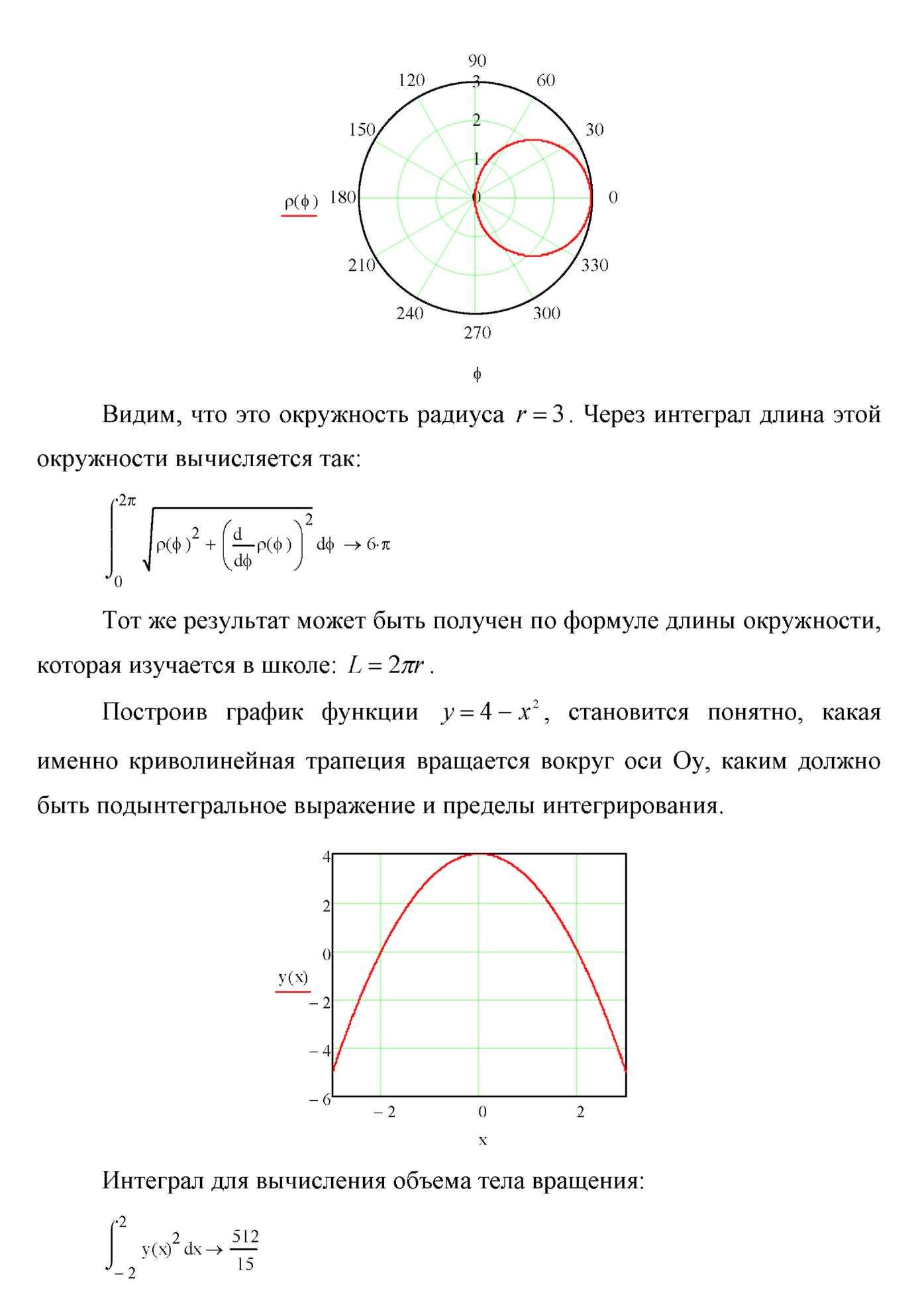
Пример 2. Найдите длину дуги

Решение:

Построим полярный график заданной функции:

Из графика видно, что это окружность радиуса r = 3. Через интеграл длина этой окружности вычисляется так:

Для проверки воспользуемся школьной формулой .

Пример 3. Найдите V тела, полученного вращением криволинейной трапеции, ограниченной линиями: ,x=0, вокруг оси Oх.

Решение:

Построим график функции :

Интеграл для вычисления объема тела вращения: