1. Техническое задание
На входе полосового фильтра действуют периодические прямоугольные радиоимпульсы (рис. 1) с параметрами:
tи = 80 мкс – длительность импульсов;
Ти = 236 мкс – период следования;
Тн = 16 мкс – период несущей частоты;
Umн = 11 В – амплитуда несущего колебания, имеющего форму гармонического uн(t) = Umнcos нt.
Требуется рассчитать двусторонне нагруженный пассивный полосовой LC-фильтр и активный полосовой RC-фильтр для выделения эффективной части спектра радиоимпульсов, лежащей в полосе частот от (fн – 1/tн) до (fн + 1/tн) (главный «лепесток спектра»).
Характеристика фильтра аппроксимируется полиномом Чебышева. Сопротивление генератора радиоимпульсов Rг и сопротивление нагрузки Rн пассивного фильтра одинаковы: Rг = Rн = R = 1000 Ом.
2. Расчет полосового lc-фильтра
Согласно заданию на курсовую работу на входе полосового фильтра действуют периодические радиоимпульсы (рис.1) с параметрами: период следования импульсов Ти = 236 мкс; длительность импульсов tи = 80 мкс; период несущей частоты Тн = 16 мкс; амплитуда колебаний несущей частоты Umн = 11 В. Фильтр должен обеспечить максимально допустимое ослабление в полосе пропускания Amax = A = 3 дБ. Полное ослабление на границах полос непропускания Апол = 45 дБ. Характеристика фильтра аппроксимируется полиномом Чебышева.
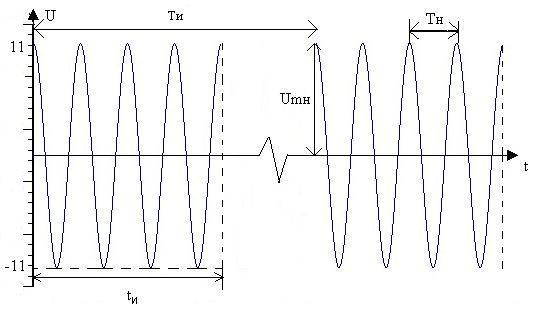
Рисунок 1 – Периодические прямоугольные радиоимпульсы с несущим колебанием uн(t) = 11cos нt
Сопротивления нагрузок фильтра слева и справа Rг = Rн = R = 600 Ом (рис. 2).
Рисунок 2 – Схема подключения фильтра к источнику сигнала
2.1. Расчет амплитудного спектра радиоимпульсов
Необходимо определить частотный состав сигнала, поступающего на вход фильтра, т.е. рассчитать и построить график амплитудного спектра периодических радиоимпульсов.
Несущая частота:
Гц = 62,5 кГц.
Рассчитываются частоты нулей огибающей спектра. Они зависят от длительности импульса:
кГц;
кГц;
кГц;
кГц.
Максимальное
значение огибающей в виде напряжения,
соответствующее частоте
,
находится по формуле:
В.
(2.1)
Зная максимальное значение и расположение нулей по оси частот, строим огибающую дискретного спектра периодических радиоимпульсов в виде пунктирной кривой в масштабе по оси частот (рис.3).
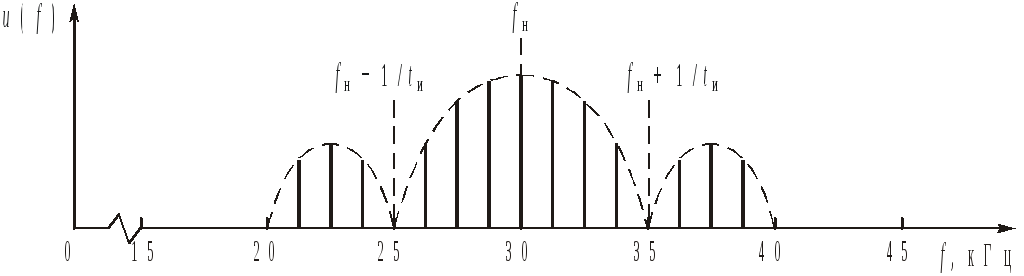
Рисунок 3 – График модуля спектральной функции U(f)=|U(jf)| радиоимпульса
Внутри огибающей
находятся спектральные составляющие
или гармоники спектра с частотами
,
где i
– номер гармоники. Они располагаются
симметрично относительно несущей
частоты, зависят от периода следования
импульсов и находятся по формуле:
.
Учитывая, что
кГц,
рассчитываем
частоты гармоник, лежащих справа от
:
кГц;
кГц;
кГц;
кГц;
кГц и т.д.
Частоты гармоник,
лежащих слева от
:
кГц;
кГц;
кГц;
кГц;
кГц и т.д.
Амплитуды напряжения i-ых гармоник находится по формуле:
(2.2)
где 
– количество периодов несущих колебаний
косинусоидальной формы в импульсе. В
рассматриваемом примере K
= 5.
Из анализа рис. 3 видно, что главный «лепесток спектра» занимает диапазон частот от 50 до 75 кГц. Крайние частоты диапазона совпадают с нулями огибающей, поэтому их амплитуды равны нулю, в частности Um.3 = 0, Um.(–3) = 0.
После расчета амплитуд по (2.2) их значения отражаются в виде дискретных составляющих внутри огибающей спектра (рис.3).