1.4. Третий канал возмущения

Так как передаточная функция объекта по третьему каналу возмущения аналогична по структуре передаточной функции W_об⁰(p), то мы можем воспользоваться формулами, которые были выведены в пункте 1.1 первого этапа части первой.

• Построения переходной функции

Воспользуемся формулой (1.1). Подставим в нее значения для объекта по третьему каналу возмущения.

(1.23)

При t < t h(t) = 0.

Таблица 1.13 - Расчетные данные для построения переходного процесса

t	10	20	30	40	50	60	70	80	90	100	110
hв3(t)	0	0,39	1,496	3,196	5,4	8,038	11,04	14,34	17,91	25,67	29,8

t	120	130	140	150	160	170	180	190	200
hв3(t)	34,06	38,43	42,91	47,46	52,1	56,76	61,5	66,26	71,07

Рис. 1.13 Переходная функция объекта по третьему каналу возмущения

• Построение амплитудно – частотной характеристики

(1.24)

Таблица 1.14 - Расчетные данные для построения АЧХ

ω	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8
Ав3(ω)	∞	0,5	0,125	0,055	0,031	0,2	0,014	0,01	7,8·10-3

ω	0,9	1,0	1,2	1,4	1,6	1,8	2,0	∞
Ав3(ω)	6,2·10-3	5,0·10-3	3,47·10-3	2,5·10-3	1,95·10-3	1,54·10-3	1,25·10-3	0

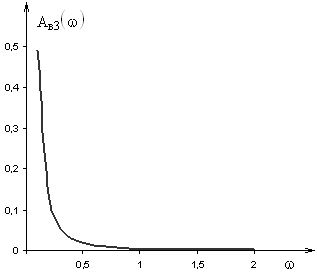
Рис. 1.14 АЧХ объекта по третьему каналу возмущения

• Построение фазо – частотной характеристики

(1.25)Таблица 1.15 - Расчетные данные для построения ФЧХ

ω	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9
φв3(ω)	-π/2	-2,976	-3,058	-3,086	-3,1	-3,11	-3,114	-3,118	-3,121	-3,123

ω	1,0	1,1	1,2	1,3	1,4	1,6	1,8	2,0	∞
φв3(ω)	-3,125	-3,126	-3,128	-3,129	-3,13	-3,131	-3,132	-3,133	-π

Рис. 1.15 ФЧХ объекта по третьему каналу возмущения

• Построение амплитудно – фазной характеристики

(1.26)

(1.27)

Таблица 1.16 - Расчетные данные для построения АФХ

ω	0	0,6	0,11	0,16	0,21	0,26	0,37	0,36	0,41
Reв3(ω)	∞	-1,31	-0,41	-0,2	-0,115	-0,075	-0,05	-0,039	-0,03
Imв3(ω)	∞	-0,04	-0,06	-0,02	-0,0092	-0,005	-0,003	-0,0018	-0,0012

Продолжение таблицы 1.16

ω	0,46	0,51	0,55	0,6	0,65	0,75	∞
Reв3(ω)	-0,024	-0,02	-0,016	-0,014	-0,012	-0,01	0
Imв3(ω)	-8,8·10-4	-6,4·10-4	-4,8·10-4	-3,8·10-4	-3·10-4	-2,4·10-4	0

Рис. 1.16 АФХ объекта по третьему каналу возмущения

Этап 2. Синтез замкнутой САУ с ПИ – регулятором на заданную степень колебательности m =0,221

2.1. Построение расширенных частотных характеристик объекта по каналу регулирования

• Построение амплитудно – частотной характеристики

Заменим р = -mω+jω в выражении передаточной функции и получим следующее выражение:

(1.28)

Находим выражение для АЧХ по каналу регулирования.

(1.29)

Таблица 1.17 - Расчетные данные для построения РАЧХ и АЧХ

ω	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0
Аоб(ω)	∞	1,857	0,49	0,22	0,124	0,08	0,055	0,041	0,031	0,025	0,02
Аоб(m,ω)	∞	2,398	0,76	0,42	0,293	0,23	0,202	0,185	0,176	0,174	0,175

ω	1,2	1,3	1,4	1,5	1,6	1,7	1,8	1,9	2,0
Аоб(ω)	0,014	0,012	0,01	8,9·10-3	7,8·10-3	6,92·10-3	6,2·10-3	5,54·10-3	5,0·10-3
Аоб(m,ω)	0,189	0,201	0,22	0,234	0,257	0,284	0,316	0,353	0,398

Рис. 1.17 АЧХ и РАЧХ объекта по каналу регулирования

• Построение фазо – частотной характеристики

Находим выражение для ФЧХ по каналу регулирования.

(1.30)

При w = == 0,181 и

Следовательно, при w ≤ 0,181

(1.31)

,

а при w > 0,181

(1.32)

.

Таблица 1.18 - Расчетные данные для построения РФЧХ и ФЧХ

ω	0	0,005	0,01	0,015	0,02	0,025	0,03	0,035	0,04	0,05
φоб(ω)	-1,57	-1,745	-1,92	-2,08	-2,23	-2,38	-2,51	-2,64	-2,76	-2,9
φоб(m,ω)	-1,18	-1,97	-2,147	-2,33	-2,5	-2,67	-2,82	-2,96	-3,09	-3,3

ω	0,06	0,07	0,09	0,1	0,15	0,16	0,17	0,18	0,19	0,2
φоб(ω)	-3,15	-3,32	-3,62	-3,76	-4,38	-4,5	-4,61	-4,72	-4,83	-4,9
φоб(m,ω)	-3,54	-3,72	-4,04	-4,18	-4,81	-4,93	-5,05	-5,16	-5,27	-5,38

Рис. 1.18 РФЧХ и ФЧХ объекта по каналу регулирования

2.2. Построение кривой равной (заданной) степени колебательности (m =0,221)

Передаточная функция ПИ – регулятора:

Заменим р = -m·ω + j ω и выделим действительную и мнимую части:

(1.33)

(1.34)

Передаточная функция объекта по каналу регулирования:

Выделим действительную и мнимую части;

Для того чтобы САУ имела заданную степень колебательности m=0,221 необходимо, чтобы АФХ разомкнутой САУ проходила через точку (-1, j0), то есть:

(1.35)

Передаточная функция разомкнутой системы имеет вид:

В этой системе три неизвестных: s₀, s₁, ω, – поэтому решая систему считаем, что ω – это параметр, и таким образом находим s₀ и s₁.

(1.36)

Преобразуем второе выражение в системе (1.35), затем подставим найденное s₀ в преобразованное выражение и найдем s₁:

(1.37)

Таблица 1.19 - Расчетные данные для построения кривой равной (заданной) степени колебательности (m =0,221)

ω	0	0,001	0,002	0,003	0,004	0,005	0,006	0,007
s0	0	2,06·10-6	8,12·10-6	1,8·10-5	3,13·10-6	4,8·10-5	6,78·10-5	9,041·10-5
s1	0	9,43·10-4	2·10-3	3,18·10-3	4,46·10-3	5,85·10-3	7,34·10-3	8,94·10-3

ω	0,008	0,009	0,01	0,015	0,02	0,025	0,026	0,027
s0	1,16·10-4	1,72·10-4	3,37·10-4	5,02·10-4	5,02·10-4	6,2·10-4	6,33·10-4	6,43·10-4
s1	0,011	0,012	0,014	0,025	0,037	0,051	0,054	0,057

ω	0,028	0,029	0,03	0,035	0,04	0,042
s0	6,47·10-4	6,47·10-4	6,41·10-4	5,11·10-4	1,77·10-4	-2,71·10-5
s1	0,06	0,063	0,066	0,081	0,096	0,102

Рис. 1.19 Кривая равной степени колебательности (m =0,221)

Так как объект по каналу регулирования является астатическим, то кривая равной степени колебательности выходит из начало координат.

3. Выбор оптимальных настроек ПИ – регулятора

Для определения оптимальных настроек ПИ-регулятора, обеспечивающих при заданной степени колебательности m=0,221 минимизацию квадратичной интегральной оценки I₂ переходного процесса в замкнутой системе, необходимо найти точку с оптимальными настройками значение частоты _опт составляет примерно 1,3_м, где _м – значение частоты в точке максимума кривой S₀-S₁ (рис. 1.19):

_м=0,028

_опт1,3_м=1,30,028=0,0364

Оптимальные настройки: S₀^опт=5,283·10^-4,

S₁^опт=0,08.

Этап 3. Анализ замкнутой САУ с оптимальными настройками ПИ – регулятора