1.2. Первый канал возмущения

• Построения переходной функции

Так как запаздывание только сдвигает переходную функцию на время t, то вывод переходной функции будем делать для аналогичного звена без запаздывания, а «t» - учтем в окончательной формуле. Таким образом, передаточную функцию объекта представим в виде:

W_в1(p)=W_в1⁰(p)×е^-pt

Х_вх(t)=1(t) – входной сигнал.

Изображение выходного сигнала имеет вид:

Рассмотрим характеристическое уравнение .

Найдем дискриминант: D = b₁² - 4×b₂ = 15² - 4×50 = 25 > 0

Следовательно, корни характеристического уравнения вещественные и имеют вид:

Определяем коэффициенты А, В, С:

Находим оригинал:

(1.8)

Учтем явление транспортного запаздывания, то есть при t ³ t переходная функция имеет вид:

(1.9)

При t < t h(t) = 0.

Таблица 1.5 - Расчетные данные для построения переходного процесса

t	6	10,7	15,4	20,1	24,8	29,8	34,2	38,9	43,6	48,3
hв1(t)	0	0,127	0,197	0,238	0,262	0,277	0,285	0,291	0,294	0,296

t	53,0	57,7	62,4	67,1	71,8	76,5	81,2	85,9	90,6	95,3	∞
hв1(t)	0,298	0,299	0,299	0,299	0,3	0,3	0,3	0,3	0,3	0,3	0,3

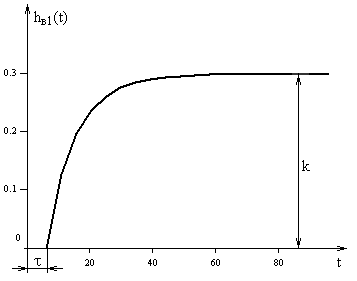
Рис. 1.5 Переходная функция объекта по первому каналу возмущения

• Построение амплитудно – частотной характеристики

Заменим р = jω в выражении передаточной функции и получим следующее выражение:

Находим выражение для АЧХ по каналу регулирования.

(1.10)

Таблица 1.6 - Расчетные данные для построения АЧХ

ω	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0
Ав1(ω)	0,3	0,221	0,148	0,108	0,085	0,069	0,058	0,05	0,044	0,039	0,036

ω	1,1	1,2	1,3	1,4	1,5	1,6	1,7	1,8	1,9	2,0	∞
Ав1(ω)	0,032	0,03	0,028	0,026	0,024	0,022	0,021	0,02	0,019	0,018	0

Рис. 1.6 АЧХ объекта по первому каналу возмущения

• Построение фазо – частотной характеристики

Находим выражение для ФЧХ по каналу регулирования.

(1.11)

При w = Ö1/b₂ = Ö1/50 = 0,1414 и

Следовательно, при w ≤ 0,1414

(1.12)

,

а при w > 0,1414

(1.13)

.

Таблица 1.7 - Расчетные данные для построения ФЧХ

ω	0	0,014	0,028	0,042	0,057	0,071	0,085	0,099	0,113	0,127
φв1(ω)	0	-0,38	-0,754	-1,114	-1,457	-1,781	-2,085	-2,37	-2,637	-2,887
ω	0,141	0,327	0,513	0,699	0,885	1,071	1,257	1,442	1,628	1,814
φв1(ω)	-3,123	-5,361	-6,913	-8,252	-9,501	-10,7	-11,88	-13,05	-14,2	-15,34

Рис. 1.7 ФЧХ объекта по первому каналу возмущения

• Построение амплитудно – фазной характеристики

Приведем W_в1(jω)к виду .

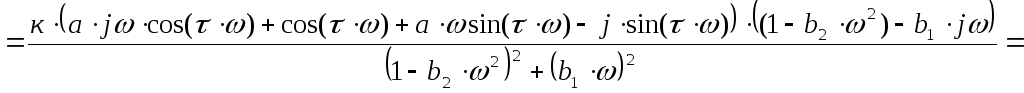
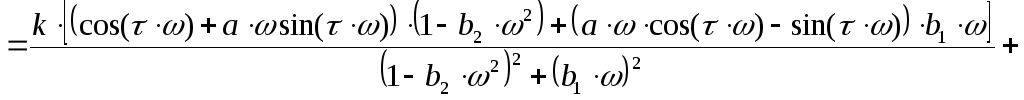
(1.14)

(1.15)

Таблица 1.8 - Расчетные данные для построения АФХ

ω	0	0,15	0,3	0,45	0,6	0,75	0,9	1,05	1,2	1,35	1,5
Reоб(ω)	0,03	-0,04	-0,107	-0,05	0,014	0,044	0,034	0,0036	-0,02	-0,03	-0,01
Imоб(ω)	0	-0,18	-0,02	0,06	0,06	0,02	-0,02	-0,034	-0,021	0,004	0,02

ω	1,65	1,8	1,95	2,1	2,25	2,4	2,55	2,7	2,85	∞
Reоб(ω)	0,008	0,019	0,015	0,0005	-0,012	-0,015	-0,006	-0,005	0,012	0
Imоб(ω)	0,02	0,005	-0,011	-0,017	-0,01	0,003	0,013	0,012	0,003	0

Рис. 1.8 АФХ объекта по первому каналу возмущения