Ifstream имя логического файла;

Открытие файла

имя логического файла.open(имя физического файла);

Закрытие файла

имя логического файла.close();

#include <cstdlib>

#include <iostream>

#include <fstream>

#include <cmath>

using namespace std;

double fun(double x);

int main()

{double a, b, h, x; char s[20];

cout << "Enter the beginning and end of the segment, step-tabulation: ";

cin >> a >> b >> h;

cout << "File name? "; cin >> s;

ofstream f;

f.open(s);

for (x=a; x<=b; x+=h)

{f.width(10); f << x;

f.width(15); f << fun(x) <<

endl; }

f.close();

system("PAUSE");

return EXIT_SUCCESS;

}

double fun(double x)

{ return x*cos(x); }

В файле abc.txt хранятся матрицы A(N,M) и B(M,K). Пусть структура файла следующая: в первой строке хранятся числа n и m, затем построчно матрица A, за тем строка, в которой хранится m и k. Затем – построчно матрица B. Найти матрицу С=A^.B и записать ее в файл rez.txt.

56. Операции с двоичными файлами

Операции с двоичными файлами

При работе с двоичными файлами в параметре mode должна быть добавлена буква b: «rb+», «wb+».

Ввод-вывод при работе с двоичными файлами осуществляется с помощью функций:

fread (void *ptr, size, n, FILE *filename)

Функция возвращает количество считанных элементов.

Функция fread считывает из файла filename в массив ptr n элементов размера size.

fwrite (const void *ptr, size, n, FILE *filename)

Функция fwrite записывает в файл filename из массива ptr n элементов размера size.

Функция возвращает количество записанных элементов.

Для контроля достижения конца файла есть функция feof.

Int feof(file * filename)

функция возвращает ненулевое значение, если достигнут конец файла.

57. Решение уравнений вида f(х)=0. Отделение корней

Отделение корней может производиться графически (путем построения графика функции f(x)) или аналитически. Для аналитического отделения корней находят все критические точки функции f(х), т. е. точки, в которых производные равны нулю или не существуют. Это можно сделать численными методами или – в несложных случаях – аналитически. Для этого f(х) дифференцируют, приравнивают производную к нулю и решают полученное уравнение относительно х. Кроме того, определяют все точки, где по тем или иным причинам (например, знаменатель обращается в нуль, под логарифмом появляется нуль и т. д.) производная может не существовать.

В этих (критических) точках или в непосредственной близости от них определяют знак функции f(х_i), т. е. находят sign f(х_i). Затем строят ряд знаков функции в критических точках, включая в рассмотрение и крайние точки числовой оси - и +. Анализируют этот ряд, и по числу смен знаков определяют количество корней (равно числу смен знаков sign f(х_i)) и интервалы, где локализованы эти корни. На левой и на правой границах такого интервала функция f(х) должна иметь разные знаки.

Пример. Дано уравнение: 5^х–6х–3 = 0. Найти количество корней и интервалы нахождения этих корней.

 Решение

Обозначим: f(х) = 5^х–6х–3. Находим производную: f'(x) = 5^х ln5–6. Вычислим корень производной:

5^х ln5 – 6 = 0; 5^х = 6/ln5;  xlg5 = lg6–lg(ln5);

х = (lg6–lg(ln5))/lg5 = (0,7782 – 0,2065)/0,6990 = 0,5717/0,6990 = 0,82.

Составим таблицу знаков функции f(х), полагая х, равным:

а) критическим значениям функции (корням производной) или близким к ним;

б) граничным значениям (исходя из области допустимых значений неизвестного).

58. Решение уравнений вида f(х)=0. Метод деления отрезка пополам

Этот метод можно рассматривать как развитие метода сканирования: величина отрезков, на которые делится весь интервал при многоэтапном применении метода сканирования, становится равной половине исходного отрезка [а, b]. В этом случае сначала исходный отрезок делится на две равные части (пополам). Затем сравнивают знаки функции на концах каждой из двух половинок и определяют ту половинку, в которой содержится решение (знаки функции на концах должны быть разные), т. е. сужаем отрезок [а, b],перенося в найденную точку конец отрезка а или b. Затем найденную половинку опять делят на две равные части, снова выбирают одну из двух половинок, содержащую корень, и т. д. Условием окончания служит заданная малость отрезка, где содержится корень.

Пример. Дано уравнение: х³ – 0,2x² + 0,5x + 1,5 = 0. Уточнить корень с погрешностью    < 0,001.

Решение. Запишем: f(х) = х³ – 0,2x² + 0,5x + 1,5.

Проведя процедуру отделения корней, получим, что корень находится в промежутке [-1; 0], т.е. a = -1, b = 0.

f(-1) = -1 – 0,2 – 0,5 + 1,5 = -0,2 < 0;

f(0) = 1,5 > 0.

 Делим интервал [-1; 0] на две части, т.е. находим х = (-1+0)/2 = -0,5. Затем определяем произведение f(a)·f(x). Если f(a)·f(x)>0, то начало интервала a переносим в точку х (а=х). Если f(a)·f(x)<0, то конец интервала b переносим в точку х (b=х). Затем новый интервал делим пополам и т.д.

59. Решение уравнений вида f(х)=0. Метод хорд

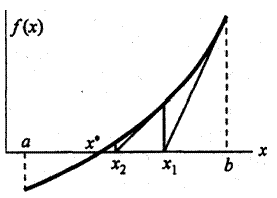
В этом методе нелинейная функция f(x) на отделенном интервале [а,b] заменяется линейной, в качестве которой берется хорда – прямая, стягивающая концы нелинейной функции. Эта хорда определяется как прямая, проходящая через точки с координатами (а,f(а)) и (b,f(b)). Имея уравнение хорды: у = cx + d, можно легко найти точку ее пересечения с горизонтальной осью, подставив в уравнение у = 0 и найдя из него x. Естественно, в полученной таким путем точке x₁ не будет решения, ее принимают за новую границу отрезка, где содержится корень. Через эту точку с координатами (x₁,f(x₁)) и соответствующую границу предыдущего интервала опять проводят хорду, находят x₂ и т. д. несколько раз, получая последовательность: х₃, х₄, х₅ ..., сходящуюся к корню. Метод применим только для монотонных функций.

60. Решение уравнений вида f(х)=0. Метод Ньютона

Идея, на которой основан метод, аналогична той, которая реализована в методе хорд, только в качестве прямой берется касательная, проводимая в текущей точке последовательности. Уравнение касательной находится по координате одной точки и углу наклона (значение производной). В качестве начальной точки в зависимости от свойств функции берется или левая точка: x₀ = а (если f(а) f"(a) > 0), или правая точка: x₀ = b (если f(b) f"(b)>0). Алгоритм записывается следующим образом:

Пример. Дано уравнение: х³ – 0,2x² + 0,5x + 1,5 = 0. Уточнить корень с погрешностью    < 0,001.

Решение. Запишем f(х) =х³ – 0,2x² + 0,5x + 1,5.

Проведя процедуру отделения корней, получим, что корень находится в промежутке [-1; 0], т. е. а = -1, b = 0.

f(-1) = -1 – 0,2 – 0,5 + 1,5 = -0,2 < 0; f(0) = 1,5 > 0.

Находим первую производную: f'(х) = 3х² – 0,4x + 0,5.

Находим вторую производную: f"(х) = 6х – 0,4.

f"(-1) = -6 – 0,4 = -6,4 < 0; f"(0) = – 0,4 = -0,4 < 0.

На конце а отрезка [а,b] выполняется условие f(-1) f"(-1) > 0, поэтому за начальное приближение примем x₀ =0,8, а вычисления будем проводить по формуле

                                               

 Предварительно найдем f'(х₀) = 3 (-1)² – 0,4 (-1) + 0,5 = 3,9.

61. Решение уравнений вида f(х)=0. Комбинированный метод

Данный метод, так же, как и предыдущие, базируется на замене нелинейной функции f(х) линейной, но с учетом стремления к корню метода хорд и метода Ньютона с разных сторон; для повышения эффективности использует оба алгоритма одновременно. Один шаг делается методом хорд, а следующий – с другой стороны – методом Ньютона. При этом интервал, где содержится корень, сокращается с обеих сторон, что обусловливает другое условие окончания поиска. Поиск можно прекратить, как только разница между правым и левым концами интервала станет меньше предварительно заданной погрешности  .

Пример. Дано уравнение: x³ – 2х² – 4х + 7 = 0. Уточнить корень с погрешностью e < 0,001.

 Решение. Проведя процедуру отделения корней, получим, что уравнение имеет три действительных корня: х₁Î[-2, -1]; x₂Î[1, 2]; х_зÎ[2, 3].

Находим первую производную:  f'(х) = 3х² – 4x – 4.

Находим вторую производную:  f"(х) = 6х – 4.

Для примера рассмотрим уточнение корня х₁. Учитывая, что f(-2) < 0;   f(-1)>0; f"(x)=6х – 4 и при –2  х  –1, – f"(x)<0, для расчетов примем следующие формулы:

где х_лi и x_пi – соответственно значение корня по недостатку (слева) и избытку (справа); х_лi = -2, x_пi = -1.

62. Решение систем линейных уравнений. Метод Якоби — метод простой итерации

63. Решение систем линейных уравнений. Метод Гаусса—Зейделя

64. Интерполяция. Интерполяция по Лагранжу

65. Численное интегрирование. Метод прямоугольников с недостатком

66. Численное интегрирование. Метод прямоугольников с избытком

67. Численное интегрирование. Метод трапеций

68. Численное интегрирование. Метод Симпсона – метод парабол.

69. Методы одномерной оптимизации

70. Метод деления отрезка пополам.

71. Метод «Золотого сечения»