5.2. Лабораторная работа № 2. Дроссельные расходомеры

Цель работы:

1. усвоить идею измерения расхода жидкости с помощью дроссельных расходомеров;

2. ознакомиться с конструкциями реальных образцов нормальных дроссельных расходомеров;

3. по результатам эксперимента получить зависимости 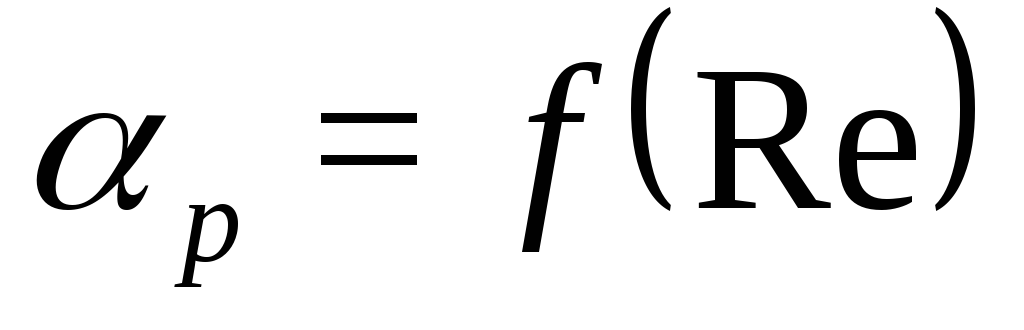или .

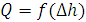4. Усвоить технику измерения действительного расхода с помощью ротаметра, дроссельных расходомеров, мерного бака, скоростного счетчика расхода жидкости.

Описание экспериментальной установки.

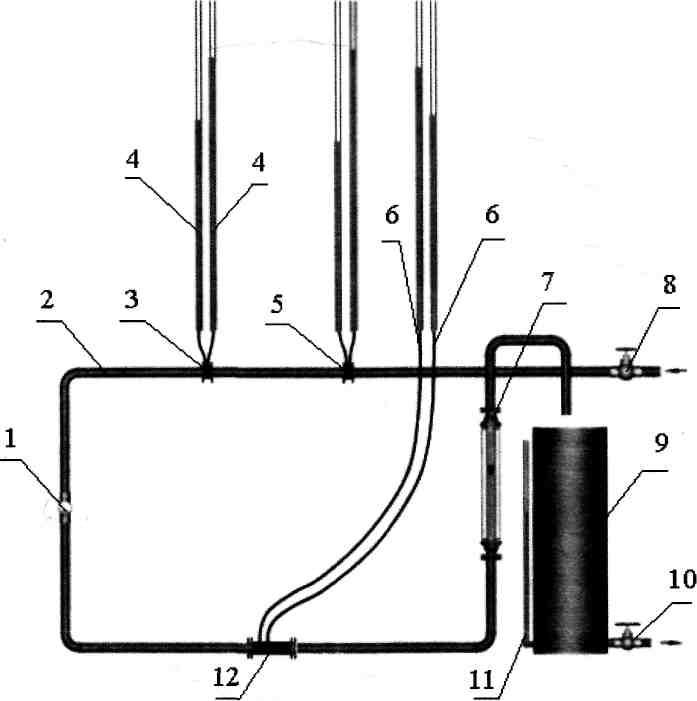
Рисунок 33 – Схема экспериментальной установки

Экспериментальная установка (рисунок 33) представляет собой трубопровод 2, на котором последовательно установлены расходомеры: труба Вентури 12, ротационный счетчик расхода жидкости 1, сопло 3, диафрагма 5, регулирующий расход жидкости вентиль 8, мерный бак 9 и ротаметр 7.

Ротаметр предназначен для измерения расхода жидкости и представляет собой стеклянную трубку, имеющую специальный внутренний профиль, внутри которой помещено твердое тело определенной формы, называемое поплавком. На внешней поверхности стеклянной трубки нанесены деления от 0 до 100. Чем больше расход жидкости через ротаметр, тем более высокое положение относительно нулевой отметки занимает поплавок. Для определения величины расхода жидкости в трубопроводе к ротаметру прилагается тарировочный график в координатах «N – число делений ротаметра» - «Q – расход жидкости» (рисунок 34). Расход жидкости в трубопроводе может быть определен по тарировочному графику или рассчитан по аппроксимирующему уравнению.

Рисунок 34 – Тарировочный график в координатах «N – число делений ротаметра» - «Q – расход жидкости»

Методика проведения эксперимента.

Объем, содержание и конкретное задание по работе определяется преподавателем. Один из вариантов задания и порядок выполнения приводится ниже.

Задание: построить экспериментальную зависимость коэффициента расхода дроссельного расходомера от критерия Рейнольдса для нормальной диафрагмы, сопла и трубы Вентури.

Для выполнения задания необходимо провести серию опытов при различных заданиях расхода жидкости, который изменяется степенью открытия вентиля 8 и измеряется с помощью ротаметра 7, для каждого значения расхода жидкости измерить соответствующий ему перепад пьезометрических напоров на дроссельном расходомере. Значение опытных величин записывается в тех единицах измерения, которые применялись при проведении опыта, при использовании этих величин в расчетах их значение необходимо привести в размерности системы СИ.

Опытные и расчетные величины удобно представить в виде таблицы, один из вариантов которой приводится ниже:

Таблица 4 – Опытные и расчетные значения процесса изучения работы дроссельных расходомеров

Параметр		Размер- ность	Номер опыта
			1	2	…
1		2	3	4	5
Измеренные величины	Положение поплавка ротаметра	дел.
	Действительный расход жидкости Qд	м3/с
	Разность пьезометрических напоров на диафрагме ∆h	мм
	Разность пьезометрических напоров на сопле ∆h	мм
	Разность пьезометрических напоров на трубе Вентури ∆h	мм

Окончание таблицы 4.

	2	3	4	5	6
Расчетные величины	Средняя скорость жидкости в трубопроводе	м/с
	Теоретическая скорость жидкости в узком сечении диафрагмы	м/с
	Теоретическая скорость жидкости в узком сечении сопла	м/с
	Теоретическая скорость жидкости в узком сечении трубы Вентури	м/с
	Теоретический расход жидкости в узком сечении диафрагмы	м3/с
	Теоретический расход жидкости в узком сечении сопла	м3/с
	Теоретический расход жидкости в узком сечении трубы Вентури	м3/с
	Коэффициент расхода диафрагмы	-
	Коэффициент расхода сопла	-
	Коэффициент расхода трубы Вентури	-
	Критерий Рейнольдса в сечении трубопровода	-

Обработка опытных данных:

1. Средняя скорость жидкости в трубопроводе:

,

где Q_д – действительный расход жидкости, определяется по по тарировочному графику или рассчитывается по аппроксимирующему уравнению, м³/с ;

- площадь сечения трубопровода, м²;

где d – диаметр трубопровода, м

2. Теоретическая скорость жидкости в узком сечении дроссельного расходомера, м/с:

,

где g – ускорение свободного падения, м/с² ;

∆h – разность пьезометрических напоров в широком и узком сечении дроссельного расходомера, м;

3. Теоретический расход жидкости, м³/с:

,

где v_Т - теоретическая скорость жидкости в узком сечении дроссельного расходомера, м/с

- площадь узкого сечения дроссельного расходомера;

где d₀ – диаметр узкого сечения дроссельного расходомера, м

4. Коэффициент расхода дроссельного расходомера:

,

где Q_д – действительный расход жидкости, м³/с;

Q_Т – теоретический расход жидкости, м³/с;

5. Критерий Рейнольдса:

,

где v – средняя скорость движения жидкости в сечении трубопровода, м/с;

d_э – эквивалентный диаметр, для трубы круглого сечения d_э=d_вн, где d_вн – внутренний диаметр опытной трубы, м;

ρ – плотность жидкости, (справочные данные);

μ – коэффициент динамической вязкости жидкости, (справочные данные), Па^.с.

Справочные данные экспериментальной установки

1. Диаметр трубопровода d=0,05, м;

2. Диаметр узкого сечения дроссельного расходомера d₀ =0,025, м;

3. Плотность воды ρ = 1000 м³/ч,

4. Коэффициент динамической вязкости (приложение А).

Контрольные вопросы по результатам выполнения работы:

1. Конструкция нормальных дроссельных расходомеров: диафрагмы, сопла, трубы Вентури.

2. Какие величины должны быть известны, чтобы определить, величину действительного расхода жидкости с помощью дроссельного расходомера?

3. Как рассчитывается теоретическая скорость жидкости в узком сечении дроссельного расходомера, и теоретический расход жидкости?

4. Какой из расходомеров обладает наибольшим гидравлическим сопротивлением?

5. Какой из расходомеров имеет наименьший коэффициент расхода?

6. Как влияет температура жидкости на величину коэффициента расхода?

7. Можно ли использовать дроссельные расходомеры для измерения расхода газов, паров?