4.4. Уравнение неразрывности (сплошности потока)

4.4.1. Уравнение неразрывности (сплошности потока) для жидкости

При рассмотрении движения жидкости считают, что в потоке жидкость сплошь заполняет занимаемое ею пространство без образования пустот, т.е. движение жидкости происходит неразрывно. В этом случае справедливо уравнение неразрывности. Дифференциальное уравнение неразрывности – это закон сохранения массы, записанный для элементарного объема жидкости.

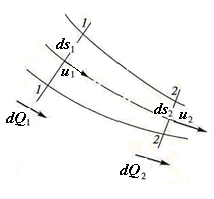
Пусть имеем элементарную струйку (рис. 16 а). Возьмем сечение 1-1 с площадью и скоростью движения частиц жидкости и₁. Элементарный расход через сечение 1-1 равен:

,

Затем возьмем сечение 2-2 в этой же струйке с площадью сечения и скоростью u₂. Элементарный расход через сечение 2-2 равен:

,

Но по свойству элементарной струйки приток и отток жидкости через ее боковую поверхность невозможен, кроме того, в отсеке 1-2, который сохраняет неизменные размеры, не образуется пустот и не происходит переуплотнений; значит количества жидкости, протекающей в единицу времени через сечения 1-1 и 2-2, должны быть одинаковы, т.е.

,

Принимая во внимание, что сечения 1-1 и 2-2 приняты произвольно, можно в общем случае для элементарной струйки написать:

,

Или

Это и есть уравнение неразрывности (сплошности) для элементарной струйки, которое читается так: элементарный расход жидкости при установившемся движении есть величина постоянная для всей элементарной струйки.

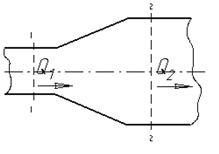
Пусть имеем поток жидкости (рис. 17 б). Взяв в потоке два произвольных сечения 1-1 и 2-2 и представив живые сечения их состоящими из суммы элементарных струек, можно написать:

–расход жидкости в сечении 1-1;

–расход жидкости в сечении 2-2.

	Q1=Q2=const
а	б
а – элементарная струйка жидкости, б – поток жидкости
Рисунок 17 – К уравнению неразрывности или сплошности потока

Но поскольку скорости касательны к боковой поверхности потока, то в отсек между сечениями 1-1 и 2-2 через боковую поверхность движения жидкости не происходит; не изменяется и объем отсека. Следовательно, в отсек через сечение 1-1 поступает столько же жидкости, сколько за то же время выходит, таким образом . Но так как сечения1-1 и 2-2 взяты произвольно, то можно написать, что или,выражая расход жидкости в сечениях через среднюю скорость получим:

Это и есть уравнение неразрывности (сплошности) для потока жидкости которое читается так: объемный расход жидкости через любое сечение потока при установившемся движении есть величина постоянная.

Из последнего уравнения для двух сечений можно написать:

,

т.е. средние скорости потока обратно пропорциональны площадям соответствующих живых сечений [2-4].

4.4.2. Уравнение неразрывности (сплошности потока) для газов

При рассмотрении движения газов секундный массовый расход газа М₁ (сечение 1-1):

где ρ₁ – плотность газа, кг/м³,

- секундный объемный расход газа.

В соответствии с условием неразрывности (сплошности) потока через сечение II-II за одну секунду выйдет масса газа:

,

равная массе газа М₁ вошедшей в сечение потока I-I. Таким образом, секундный массовый расход газа через любое сечение есть величина постоянная.

,

Это выражение называется уравнением неразрывности или уравнением постоянства расхода для газа[3,4] .