Материалы III семестра / Teoria_elektrichesky_tsepey_Neyman_1ch

184 Часть 2. Теория линейных электрических цепей

Общее решение i(t) этого уравнения, как всякого линейного дифференциального уравнения, складывается из частного решения i (t), определяемого видом функции u(t), и полного интеграла i (t) однородного дифференциального уравнения, получаемого, если принять u(t) 0. Как будет показано в гл. 9, после включения цепи под действие напряжения u(t) составляющая тока i (t) быстро затухает, умень-

Ðèñ. 4.10 шаясь до нуля практически за доли секунды или за несколько секунд. Действительно, при u 0, r 0 процесс в цепи может су-

ществовать только за счет запасов энергии в полях цепи и будет затухать вследствие рассеяния энергии на участке с сопротивлением r.

Таким образом, спустя небольшой промежуток времени после включения

âцепи устанавливается ток i(t), определяемый частным решением i (t) уравнения цепи. Величина i (t) является т о к о м у с т а н о в и в ш е г о с я р е ж и м а

âц е п и. Первые пять глав настоящей части посвящены исследованию установившихся режимов.

Пусть приложенное к цепи напряжение изменяется по синусоидальному за-

êîíó u Um sin (0t + Αu). При этом ток установившегося режима также будет синусоидальным с той же частотой 0 и, следовательно, может быть выражен в виде i Im sin (0t + Αi) Im sin (0t + Αu – 2). Задача заключается в отыскании величин Im è 2 при заданных величинах Um, 0 è Αu.

Как было сказано раньше, при исследовании установившегося синусоидального процесса начальная фаза Αu приложенного напряжения может быть выбрана произвольно. Так как в данном случае общим для всех участков является ток, то целесообразно выбрать Αu 2, чтобы начальная фаза тока была равна нулю, т. е. Αi 0. Тогда

Так как все члены, кроме двух последних в левой части уравнения, не содержат постоянных составляющих, то 01C Im + uC (0) 0.

Это уравнение должно быть справедливо для любого момента времени t. Ïî-

Возведя первое и второе равенства в квадрат и сложив, будем иметь

откуда находим связь между амплитудами тока и напряжения:

Поделив обе части этого выражения на 2, получим аналогичную связь между действующими током и напряжением:

Корень следует брать всегда со знаком «плюс», так как амплитуды и действующие значения напряжения и тока считаем положительными величинами.

Поделив второе равенство на первое, находим

tg 2 0L 1 0C . r

В выражениях, связывающих амплитуды Um è Im или действующие значения U è I напряжения и тока, в знаменателе стоит величина, имеющая размерность электрического сопротивления. Ее обозначают через z и называют п о л н ы м с о п р о т и в л е н и е м цепи. Для рассмотренной цепи

В общем случае в цепи переменного тока полное сопротивление z больше сопротивления r и может быть ему равно только в частном случае. Причина этого состоит в том, что в рассматриваемой цепи приложенное напряжение имеет не

только составляющую ir, но также составляющую L dtdi, преодолевающую ЭДС

самоиндукции, и составляющую q/C, равную напряжению на конденсаторе. Сопротивление r называют а к т и в н ы м с о п р о т и в л е н и е м цепи, так

как только им определяются необратимые активные процессы в цепи, в данном

цепи и обозначают x. Ïðè ýòîì ÷ëåí 0L, учитывающий реакцию самоиндук-

ции, называют и н д у к т и в н ы м с о п р о т и в л е н и е м цепи и обозначают xL, à ÷ëåí 1/(0C), учитывающий реакцию емкости, называют е м к о с т н ы м с о -

п р о т и в л е н и е м цепи и обозначают xC.

186 Часть 2. Теория линейных электрических цепей

Итак, имеем

Заметим, что возрастание xL при увеличении частоты объясняется тем, что ЭДС самоиндукции пропорциональна скорости изменения тока, и следовательно, ее амплитуда растет с увеличением частоты при неизменной амплитуде тока. Убывание величины xC при увеличении частоты является результатом того, что ток смещения в конденсаторе пропорционален скорости изменения напряжения на зажимах конденсатора и, следовательно, его амплитуда растет с увеличением частоты

при неизменной амплитуде напряжения.

Структура выражения для z может быть уяснена, если рассмотреть сдвиги фаз напряжений на отдель-

Ðèñ. 4.11 ных участках цепи по отношению к току. С целью наглядности построим векторную диаграмму для рас-

сматриваемой цепи. Здесь и в последующем диаграмму будем строить для действующих величин. Для краткости векторы, изображающие ток, напряжение и ЭДС, будем называть просто вектором тока, вектором напряжения и вектором ЭДС

Направим вектор тока I по вертикальной оси (рис. 4.11).

Напряжение на участке с сопротивлением r

ur ri rI m sin0t

совпадает по фазе с током, и поэтому вектор этого напряжения U r направлен

опережает ток на угол /2, и вектор этого напряжения U L должен быть повер-

нут относительно вектора тока на угол /2 в положительном направлении.

Напряжение на участке с емкостью С

отстает от тока на угол /2, и вектор этого напряженияUC должен быть повер-

нут относительно вектора тока на угол /2 в отрицательном направленèи. Складывая геометрически âåкторы напряжений на участках цепиU r ,U L èUC ,

получаем вектор напряжåíèÿU на зажимах всей цепи, который сдвинут по отношению к вектору тока I íà óãîë 2 . То обстоятельство, что величины xL 0L è xC 1/(0C) входят в выражение для реактивного сопротивления с разными знаками, объясняется тем, что напряжения uL è uC сдвинуты друг относительно

друга на угол и, следовательно, в любой момент времени противоположны друг другу, что, в частности, видно из векторной диаграммы.

Напряжения ur è (uL + uC) сдвинуты друг относительно друга на угол /2. Поэтому полное сопротивление цепи z нельзя определять путем арифметического

сложения r è x, а следует вычислять по формуле z r 2 x 2 . Зафиксируем особо внимание на следующих весьма важных результатах:

<на участке с активным сопротивлением ток совпадает по фазе с напряжением на этом участке;

<в индуктивной катушке ток отстает по фазе на угол /2 от напряжения на катушке;

<в конденсаторе ток опережает по фазе на угол /2 напряжение на зажимах конденсатора.

Рассмотрим теперь сдвиг фаз 2 между током и напряжением на зажимах всей цепи. Ток совпадает по фазе с приложенным напряжением только при x 0, т. е. или при отсутствии в цепи реактивных сопротивлений, или при их взаимной компенсации. Последнее имеет место при р е з о н а н с е, явление которого будет рассмотрено в гл. 6. Действительно, из векторнîé диаграммы (рис. 4.12) виднî, ÷òî ïðè x 0L – 1/0C 0 сумма векторов U L è UC будет равна нулю и вектор U

приложенного напряжения совпадет по направлению с вектором I тока, т. е. угол 2 будет равен нулю. Кривые тока и напряжения для этого случая изображены также на рис. 4.12. Если 0L > 1/(0C), òî x > 0, /2 Β 2 > 0 è ток отстает по фазе от напряжения на зажимах цепи. Этот случай изображен на рис. 4.13. Если же 1/(0C) > 0L, òî x < 0, – /2 4 2 < 0 è ток опережает по фазе напряжение на зажимах цепи. Этот случай изображен на рис. 4.14.Таким образом, пределами, между которыми лежит 2, являются + /2 и – 2.

4.5. Установившийся синусоидальный ток в цепи с параллельным соединением участков g, L è C

Рассмотрим цепь, изображенную на рис. 4.15, состоящую из трех параллельно соединенных участков; причем предположим, что первый участок обладает только проводимостью g, второй — только емкостью C и третий — только индуктивностью L.

188 Часть 2. Теория линейных электрических цепей

Применяя первый закон Кирхгофа, имеем

ig iC iL i.

Токи в ветвях можно выразить через приложенное напряжение. Ток в пер-

Таким образом, дифференциальное уравнение рассматриваемой цепи имеет вид

du 1

t

gu C dt L 0 u dt iL (0) i.

Пусть к цепи приложено синусоидальное напряжение u Um sin 0t . Ïðè ýòîì òîê i также будет синусоидальным и может быть представлен в виде i Im sin (0t – 2). В данном случае целесообразно принять начальную фазу приложенного напряжения равной нулю (Αu 0), так как напряжение является общим для всех ветвей.

Подставив эти выражения в уравнение цепи, получим

Так как все члены, кроме двух последних в левой части уравнения, не содержат постоянных составляющих, то 01L Um + iL(0) 0.

Уравнение цепи справедливо для любого момента времени t. Полагая 0t /2 è 0t 0, находим

Возведя первое и второе равенства в квадрат и сложив, получим

Поделив обе части этого выражения на 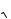2, получим связь между действующими током и напряжением:

называют п о л н о й п р о в о д и м о с т ь ю цепи. Проводимость g называют а к -

ность проводимости, называют р е а к т и в н о й п р о в о д и м о с т ь ю цепи и обозначают b. Ïðè ýòîì ÷ëåí 1/(0L) называют и н д у к т и в н о й п р о в о д и -

м о с т ь ю и обозначают bL, à ÷ëåí 0C называют е м к о с т н о й п р о в о д и м о - с т ь ю и обозначают bC. Имеем

На рис. 4.16 изображена векторная диаграмма для этой цепи для случая 1/(0L) > 0C. Ток в первом участке совпадает по фазе с напряжением, ток в конденсаторе опережает по фазе на угол /2 напряжение, а ток в катушке отстает по фазе на угол /2 от напряже-

ния. То обстоятельство, что b образуется как разность bL è bC , объясняется тем, что токи в конденсаторе и в катушке сдвинуты друг относительно друга на угол , т. е. в любой момент времени направлены по отношению к общим зажимам второй и третьей ветвей в противоположные стороны. Эти токи сдвинуты относительно тока в первой ветви на угол /2, вследствие чего полная проводимость определяется не арифметическим сложением g è b, а формулой

y g2 b2 .

Ïðè bL bC имеет место резонанс â öåïè è òîê i равен току ig в первой ветви. При 1/(0L) > 0C ток через катушку больше тока через конденсатор (рис. 4.16) и общий ток i отстает по фазе на угол 2 от напряжения, причем 0 < 2 4 /2. Ïðè 0C > 1/(0L) ток через конденсатор больше тока через катушку и общий ток i опережает по фазе напряжение, причем – /2 4 2 < 0.

4.6. Активная, реактивная и полная мощности

À ê ò è â í î é ì î ù í î ñ ò ü þ P в электрической цепи при периодических процессах называют среднее значение мощности за полный период:

ãäå p ui — ì ã í î â å í í à ÿ ì î ù í î ñ ò ü.

190 Часть 2. Теория линейных электрических цепей

Если напряжение u на зажимах цепи и ток i в цепи являются синусоидальными функциями времени: u Um sin 0t; i Im sin (0t – 2), òî

T

Учитывая, что cos(20t 2) dt 0, получаем выражение для активной мощно-

0

сти при синусоидальном процессе:

PUI cos 2.

Ìí î æ è ò å ë ü cos 2 называют к о э ф ф и ц и е н т о м м о щ н о с т и. Так как cos 2 4 1, òî P 4 UI. Только в предельном случае, когда 2 0 è cos 2 1, имеем P UI. В другом предельном случае, когда 2 ± /2 è cos 2 0, имеем P 0.

Электрические машины, трансформаторы и другие электротехнические устройства рассчитывают на определенное номинальное напряжение U, обусловленное изоляцией этих устройств, и на определенный номинальный ток I, обусловленный нагревом проводников этих устройств. Соответственно, наивысшее использование генерирующих и преобразующих электромагнитную энергию устройств будет в случае, когда коэффициент мощности приемников, на которые они работают, равен единице.

Максимальное приближение к единице коэффициента мощности предприятий, являющихся приемниками энергии, может быть осуществлено путем рационального конструирования оборудования этих предприятий, а также рациональной организацией их работы, например максимальной загрузкой двига-

телей, так как при холостом ходе cos 2 двигателей обычно низок.

Так как обычно для предприятий 2 > 0 и, следовательно, ток имеет индуктивный характер, то радикальной мерой повышения cos 2 может быть установка на этих предприятиях конденсаторов, включаемых параллельно другим устройствам.

Из диаграммы на рис. 4.11 имеем U cos 2 Ur Ir, и из диаграммы на рис. 4.16 получаем I cos 2 Ug. Следовательно, для активной мощности можем написать следующие выражения:

P UI cos 2 I 2 r U 2 g.

Величину S UI называют п о л н о й м о щ н о с т ь ю. Смысл введения понятия полной мощности ясен из сказанного выше. Если под U è I понимать номинальные значения, т. е. допускаемые при номинальном режиме действующие значения напряжения и тока электрической машины, трансформатора или других преобразователей энергий, то произведение S UI дает наибольшую возможную активную их мощность при наиболее благоприятных условиях, т. е. при cos 2 1.

Имеем следующие выражения для полной мощности:

S UI I 2 z U 2 y.

Вводят в рассмотрение еще так называемую р е а к т и в н у ю м о щ н о с т ь Q UI sin 2.

Практическое значение введения понятия реактивной мощности вытекает, например, из следующего. Обычный счетчик энергии дает значение энергии, отданной приемнику за некоторый промежуток времени ,. Эту энергию можно записать в форме

,,

P dt UI cos 2 dt,

0 0

если заметное изменение P происходит только за большое число периодов T тока и если, соответственно, , во много раз превосходит T. Однако показания такого счетчика не дают возможности судить о том, при каком коэффициенте мощности cos 2 работает потребитель энергии. Такая оценка возможна, если наряду с обычным счетчиком, показывающим действительную энергию, передаваемую приемнику, включить на зажимы приемника счетчик, показывающий величину интеграла реактивной мощности Q за тот же промежуток времени ,:

,,

Q dt UI sin 2 dt.

0 0

Очевидно, чем больше показание этого счетчика по сравнению с показанием обычного счетчика, тем ниже среднее значение cos 2 приемника за рассматриваемый промежуток времени.

Величину P можно измерить с помощью обычного ваттметра, а величину Q — с помощью специально предназначенного для этой цели электроизмерительного прибора. Зная P è Q, можно определить sin 2 è cos 2 потребителя энергии в момент измерения. Однако представляет интерес именно знать характер работы потребителя за длительный промежуток времени. С этой целью и используются счетчики, дающие названные интегральные величины.

Понятием реактивной мощности Q широко пользуются также при расчете электрических сетей переменного тока.

Из диаграммы на рис. 4.11 имеем U sin 2 Ix, и из диаграммы рис. 4.16 полу- чаем I sin 2 Ub. Следовательно, для реактивной мощности существуют выражения

Q UI sin 2 I 2 x U 2 b.

Для приемников энергии P è S всегда положительны, но реактивная мощность Q положительна лишь при 2 > 0, т. е. для индуктивных цепей, а при 2 < 0, т. е. для емкостных цепей, она отрицательна.

Заметим, что при 2 ± /2, например для конденсаторов или катушек без потерь, абсолютное значение реактивной мощности совпадает с полной мощностью.

Обратим внимание, что понятие активной мощности как средней за период T мощности справедливо для любых периодических напряжений и токов определенной частоты f 1/T и не обязательно синусоидальных. Понятие же реактивной мощности Q â âèäå Q UI sin 2, так же как и выражение активной мощности в форме P UI cos 2, справедливо лишь при синусоидальном процессе.

При выводе всех вышеприведенных соотношений предполагалось, что на зажимах цепи действует напряжение U. Если предположить, что к зажимам цепи

192 Часть 2. Теория линейных электрических цепей

приключен идеальный источник синусоидальной ЭДС, имеющей действующее значение E, то все соотношения останутся в силе с заменой U íà Å, например:

4.7. Мгновенная мощность и колебания энергии в цепи синусоидального тока

Мгновенная мощность p ui цепи переменного тока является функцией времени. Рассмотрим энергетические процессы в цепи, состоящей из последовательно соединенных участков r, L è C (рис. 4.17). Уравнение для напряжений в этой

цепи имеет вид

u ur uL uC ri L dtdi Cq .

Соответственно, для мгновенных мощностей на зажимах цепи и на отдельных участках цепи получим уравнение

Из последнего выражения видим, что мощность pr i2r на участке с сопротив-

ïðè pC > 0 скорость поступления энергии в электрическое поле конденсатора, а при pC < 0 — скорость возвращения энергии из этого поля.

Пусть напряжение u è òîê i являются синусоидальными функциями времени:

u U m sin 0t 2 ; i I m sin0t.

Здесь, так же как и в § 4.4, начальная фаза тока принята равной нулю (Αi 0), что удобно, так как ток является общим для всех участков цепи. При этом на- чальная фаза напряжения u оказывается равной 2 (Αu 2). Мгновенные напряжения на отдельных участках при этом равны (см. § 4.4):

Соответственно, для мгновенных мощностей на отдельных участках цепи получаем выражения