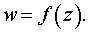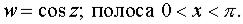задания по ТФКП для ПМ-2 курс, Ф-3 курс
.pdf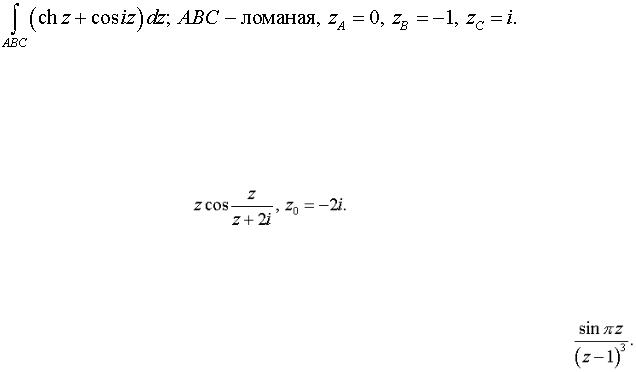
ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
ПМ, Ф |
ВАРИАНТ № 12
Задача 1. Найти все значения корня. 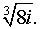
Задача 2. Представить в алгебраической форме. 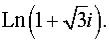
Задача 3. Представить в алгебраической форме. 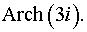
Задача 4. Вычертить область, заданную неравенствами. 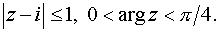
Задача 5. Определить вид кривой. 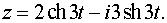
Задача 6. Восстановить аналитическую в окрестности точки z0 функцию f(z) по известной действительной части u(x,y) или мнимой v(x,y) и значению f(z0) 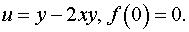
Задача 7. Вычислить интеграл от функции комплексного переменного по данной кривой.
Задача 8. Найти все лорановские разложения данной функции
а) по степеням z 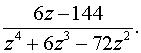 б) по степеням z - zo
б) по степеням z - zo 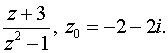
в) в окрестности точки zo
Задача 9. Определить тип особой точки z = 0 для данной функции. 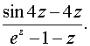
Задача 10. Для данной функции найти изолированные точки и определить их тип.
Задача 11. Вычислить интеграл. а) 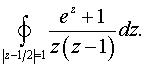 б)
б) 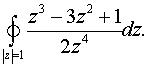
в) 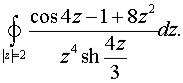 г)
г) 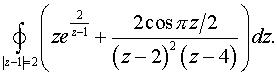 д)
д) 

ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
ПМ, Ф |
е) 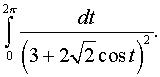 ж)
ж) 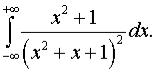 з)
з) 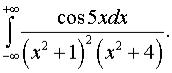
Задача 12. По данному графику оригинала найти изображение.
Задача 13. Найти оригинал по заданному изображению 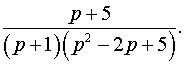
Задача 14. Найти решение дифференциального уравнения, удовлетворяющего условиям
y(0) = 0, y’(0) = 0.
Задача 15. Операционным методом решить задачу Коши 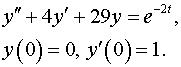
Задача 16. Материальная точка массы 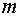 движется прямолинейно, отталкиваясь от начала координат с силой
движется прямолинейно, отталкиваясь от начала координат с силой 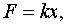 пропорциональной расстояниб. Наточку действует сила сопротивления среды
пропорциональной расстояниб. Наточку действует сила сопротивления среды 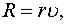 пропорциональная скорости
пропорциональная скорости 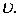 При
При 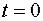 расстояние точки от начала координат
расстояние точки от начала координат 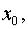 а скорость
а скорость 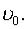 Найти закон движения
Найти закон движения 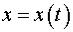 материальной точки.
материальной точки.
Задача 17. Решить систему дифференциальных уравнений
Задача 18. Выяснить, во что преобразуется геометрическая фигура при отображении с помощью функции 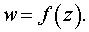
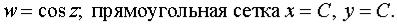

ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
ПМ, Ф |
ВАРИАНТ № 13 |
|
Задача 1. Найти все значения корня. |
|
Задача 2. Представить в алгебраической форме. |
|
Задача 3. Представить в алгебраической форме.
Задача 4. Вычертить область, заданную неравенствами. 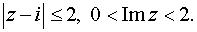
Задача 5. Определить вид кривой. 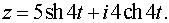
Задача 6. Восстановить аналитическую в окрестности точки z0 функцию f(z) по известной действительной части u(x,y) или мнимой v(x,y) и значению f(z0). 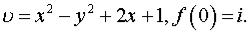
Задача 7. Вычислить интеграл от функции комплексного переменного по данной кривой.
Задача 8. Найти все лорановские разложения данной функции
а) по степеням z 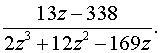 б) по степеням z - zo
б) по степеням z - zo 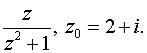
в) в окрестности точки zo
Задача 9. Определить тип особой точки z = 0 для данной функции. 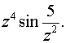
Задача 10. Для данной функции найти изолированные точки и определить их тип.
Задача 11. Вычислить интеграл. а) 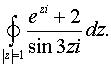 б)
б) 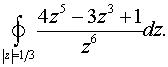 в)
в) 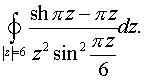
г) |
д) |
е) |

ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
ПМ, Ф |
ж) 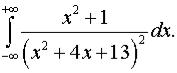 з)
з) 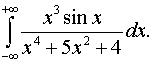
Задача 12. По данному графику оригинала найти изображение.
Задача 13. Найти оригинал по заданному изображению 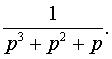
Задача 14. Найти решение дифференциального уравнения, удовлетворяющего условиям
y(0) = 0, y’(0) = 0.
Задача 15. Операционным методом решить задачу Коши 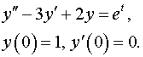
Задача 16. Материальная точка массы 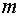 движется прямолинейно, отталкиваясь от начала координат с силой
движется прямолинейно, отталкиваясь от начала координат с силой 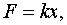 пропорциональной расстоянию. Наточку действует сила сопротивления среды
пропорциональной расстоянию. Наточку действует сила сопротивления среды 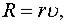 пропорциональная скорости
пропорциональная скорости 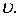 При
При 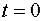 расстояние точки от начала координат
расстояние точки от начала координат  а скорость
а скорость  Найти закон движения
Найти закон движения 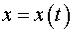 материальной точки.
материальной точки.
Задача 17. Решить систему дифференциальных уравнений
Задача 18. Выяснить, во что преобразуется геометрическая фигура при отображении с помощью функции 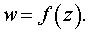
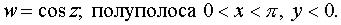

ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
ПМ, Ф |
|
|
ВАРИАНТ № 14 |
|
Задача 1. Найти все значения корня. |
|
|
Задача 2. |
Представить в алгебраической форме. |
|
Задача 3. |
Представить в алгебраической форме. |
|
Задача 4. |
Вычертить область, заданную неравенствами. |
|
Задача 5. Определить вид кривой. 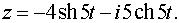
Задача 6. Восстановить аналитическую в окрестности точки z0 функцию f(z) по известной действительной части u(x,y) или мнимой v(x,y) и значению f(z0) 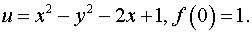
Задача 7. Вычислить интеграл от функции комплексного переменного по данной кривой.
Задача 8. Найти все лорановские разложения данной функции
а) по степеням z 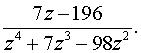 б) по степеням z - zo
б) по степеням z - zo 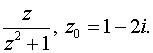
в) в окрестности точки zo
Задача 9. Определить тип особой точки z = 0 для данной функции. 
Задача 10. Для данной функции найти изолированные точки и определить их тип.
Задача 11. Вычислить интеграл а) |
б) |
в) 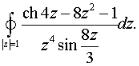 г)
г) 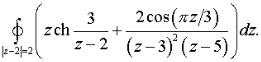 д)
д) 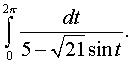
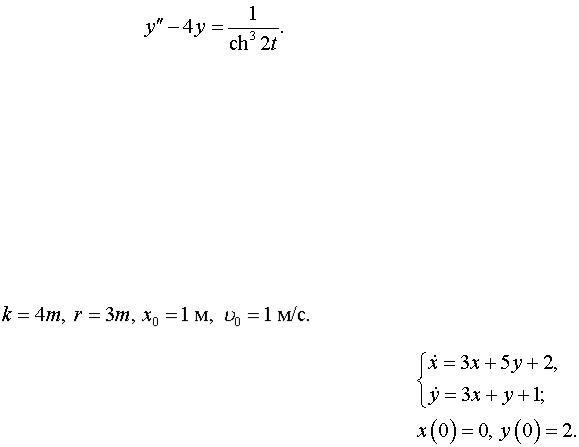
ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
ПМ, Ф |
е) 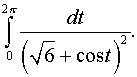 ж)
ж)  з)
з) 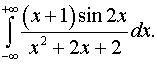
Задача 12. По данному графику оригинала найти изображение. 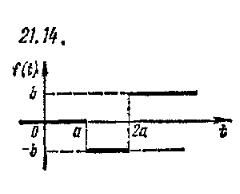
Задача 13. Найти оригинал по заданному изображению 
Задача 14. Найти решение дифференциального уравнения, удовлетворяющего условиям
y(0) = 0, y’(0) = 0.
Задача 15. Операционным методом решить задачу Коши 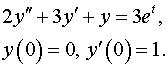
Задача 16. Материальная точка массы 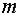 движется прямолинейно, отталкиваясь от начала координат с силой
движется прямолинейно, отталкиваясь от начала координат с силой 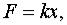 пропорциональной расстояниб. Наточку действует сила сопротивления среды
пропорциональной расстояниб. Наточку действует сила сопротивления среды 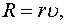 пропорциональная скорости
пропорциональная скорости 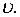 При
При 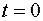 расстояние точки от начала координат
расстояние точки от начала координат 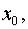 а скорость
а скорость 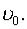 Найти закон движения
Найти закон движения 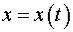 материальной точки.
материальной точки.
Задача 17. Решить систему дифференциальных уравнений
Задача 18. Выяснить, во что преобразуется геометрическая фигура при отображении с помощью функции 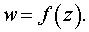
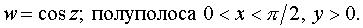
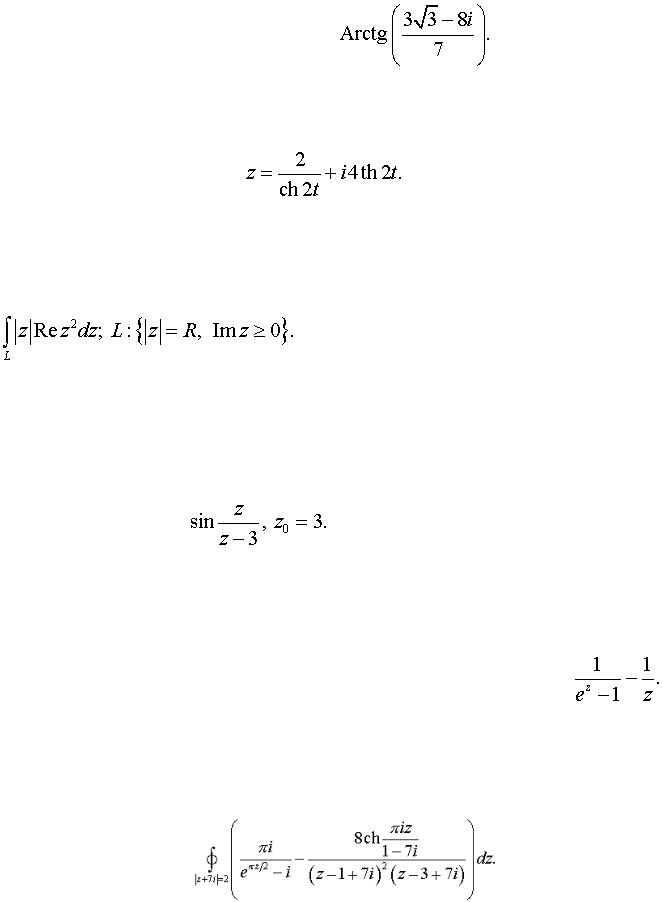
ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
ПМ, Ф |
ВАРИАНТ № 15 Задача 1. Найти все значения корня. 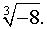
Задача 2. Представить в алгебраической форме. 
Задача 3. Представить в алгебраической форме.
Задача 4. Вычертить область, заданную неравенствами. 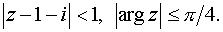
Задача 5. Определить вид кривой.
Задача 6. Восстановить аналитическую в окрестности точки z0 функцию f(z) по известной действительной части u(x,y) или мнимой v(x,y) и значению f(z0). 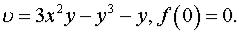
Задача 7. Вычислить интеграл от функции комплексного переменного по данной кривой.
Задача 8. Найти все лорановские разложения данной функции
а) по степеням z 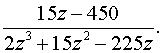 б) по степеням z - zo
б) по степеням z - zo 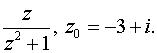
в) в окрестности точки zo
Задача 9. Определить тип особой точки z = 0 для данной функции. 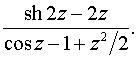
Задача 10. Для данной функции найти изолированные точки и определить их тип.
Задача 11. Вычислить интеграл а) 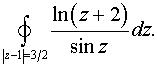 б)
б) 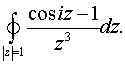
в) 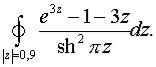 г)
г)

ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
ПМ, Ф |
д) 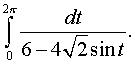 е)
е) 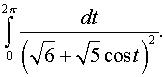 ж)
ж) 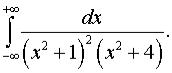 з)
з)
Задача 12. По данному графику оригинала найти изображение. 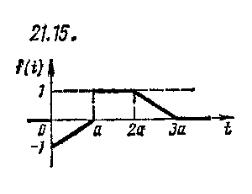
Задача 13. Найти оригинал по заданному изображению 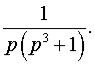
Задача 14. Найти решение дифференциального уравнения, удовлетворяющего условиям
y(0) = 0, y’(0) = 0.
Задача 15. Операционным методом решить задачу Коши 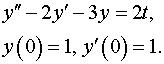
Задача 16. Материальная точка массы 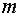 движется прямолинейно, отталкиваясь от начала координат с силой
движется прямолинейно, отталкиваясь от начала координат с силой 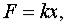 пропорциональной расстоянию. На точку действует сила сопротивления среды
пропорциональной расстоянию. На точку действует сила сопротивления среды 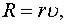 пропорциональная скорости
пропорциональная скорости 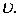 При
При 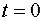 расстояние точки от начала координат
расстояние точки от начала координат 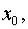 а скорость
а скорость 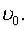 Найти закон движения
Найти закон движения 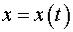 материальной точки
материальной точки
Задача 17. Решить систему дифференциальных уравнений
Задача 18. Выяснить, во что преобразуется геометрическая фигура при отображении с помощью функции 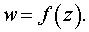
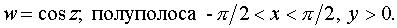

ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
ПМ, Ф |
ВАРИАНТ № 16
Задача 1. Найти все значения корня 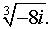
Задача 2. Представить в алгебраической форме. 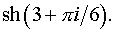
Задача 3. Представить в алгебраической форме. 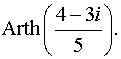
Задача 4. Вычертить область, заданную неравенствами.
Задача 5. Определить вид кривой. 
Задача 6. Восстановить аналитическую в окрестности точки z0 функцию f(z) по известной действительной части u(x,y) или мнимой v(x,y) и значению f(z0) 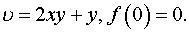
Задача 7. Вычислить интеграл от функции комплексного переменного по данной кривой.
Задача 8. Найти все лорановские разложения данной функции
а) по степеням z 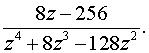 б) по степеням z - zo
б) по степеням z - zo 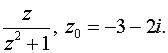
в) в окрестности точки zo
Задача 9. Определить тип особой точки z = 0 для данной функции. 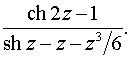
Задача 10. Для данной функции найти изолированные точки и определить их тип.
Задача 11. Вычислить интеграл а) |
б) |
в) |
г) |
д) |
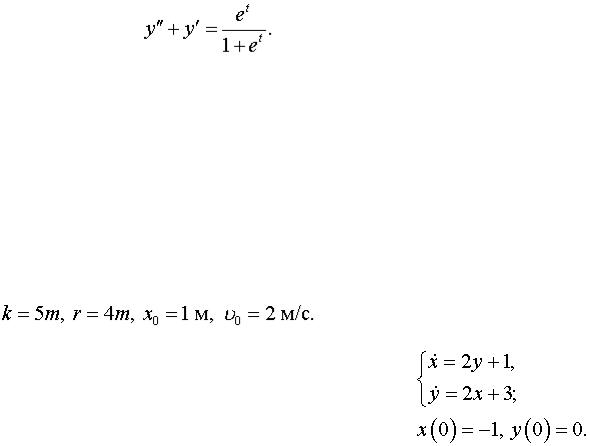
ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО |
ПМ, Ф |
е) 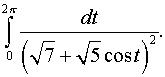 ж)
ж) 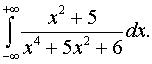 з)
з) 
Задача 12. По данному графику оригинала найти изображение. 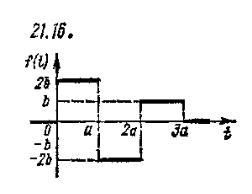
Задача 13. Найти оригинал по заданному изображению 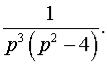
Задача 14. Найти решение дифференциального уравнения, удовлетворяющего условиям
y(0) = 0, y’(0) = 0.
Задача 15. Операционным методом решить задачу Коши 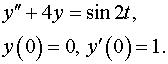
Задача 16. Материальная точка массы 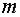 движется прямолинейно, отталкиваясь от начала координат с силой
движется прямолинейно, отталкиваясь от начала координат с силой 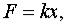 пропорциональной расстояниб. Наточку действует сила сопротивления среды
пропорциональной расстояниб. Наточку действует сила сопротивления среды 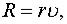 пропорциональная скорости
пропорциональная скорости 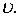 При
При 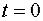 расстояние точки от начала координат
расстояние точки от начала координат 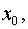 а скорость
а скорость 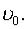 Найти закон движения
Найти закон движения 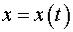 материальной точки.
материальной точки.
Задача 17. Решить систему дифференциальных уравнений
Задача 18. Выяснить, во что преобразуется геометрическая фигура при отображении с помощью функции