Lekcii_DIFFOP

Рис. 12.20

Как и при решении предыдущей задачи 12.11, исследование с помощью производных должно либо подтвердить, либо опровергнуть исследование, провед¨енное с помощью пределов. То есть, нужно убедиться, что первая производная, которая пока не найдена, положительна во всей области определения (то есть функция действительно возрастает). Что вторая производная (которая пока не найдена тоже) положительна в левой полуплоскости и отрицательна в правой (а значит график действительно в левой полуплоскости выпуклый вниз, а в правой выпуклый вверх).

III.1 Прежде, чем искать первую производную, выполним преобразование представления функции

Из полученного представления очевидно, что первая производная функции больше нуля, как сумма двух квадратов.

IV.1 Кроме того, легко найти вторую производную:

Так как знаменатель второй производной есть многочлен неч¨етной степени, то видно, что слева от 1 вторая производная положительна, а справа отрицательна. Что потверждает правильность выводов, полученных с помощью пределов.

11. Если знать об этом представлении, то можно было бы легко найти наклонную асимптоту без исследования пределов (таким образом е¨ искали в XVII-XVIII веках (а также в средних школах до 1970-х годов XX-го столетия)).

2. Конечно, производную можно найти и без преобразования, как производную частного:

не забыв при этом доказать, что дискриминант числителя меньше нуля).

21

V. Найдем точки пересечения графика с осями координат. Решим уравнение q(x) = 0. Дробь равна нулю, когда е¨ числитель равен нулю. Поэтому x2 2x = 0. Так как это уравнение квадратное, то оно имеет два корня: x = 0 и x = 2. То есть график пересекает ось абсцисс в точках (0; 0) и (2; 0). При этом стало известно, в какой точке пересекается ось ординат.

Y

X

Рис. 12.21

По двум последним задачам 12.10 и 12.11 могло сложиться впечатление, что производные при построении графиков совсем не нужны. Но прежде, чем делать такие выводы рассмотрим следующую задачу.

Задача 12.12. С помощью общей схемы исследовать функцию

'(x) = x2 + 4x + 5 x + 2

и построить на основании исследования схематический график функции. Решение. При исследовании данной функции с помощью пределов, можно, найдя область е¨ определения D' = (1; 2)[( 2; 1), вертикальную асимптоту x = 2 и наклонную асимптоту y = x 2, построить

К сожалению, пределы не позволяют найти координаты локальных экстремумов функции (хотя и позволяют обнаружить их существование). III.1 Как и в предыдущих задачах, прежде, чем найти первую производную, выполним преобразование функции

22

из которого следует, что x1 = 3 и x2 = 1.

III.3 Определим интервалы монотонности, решив неравенства.

'0(x) < 0 , x 2 (1; 3) [ ( 1; 1) ) '(x) убывает,

если x 2 x 2 (1; 3) и x 2 ( 1; 1):

III.4. Из эскиза (12.23) видно, что в стационарных точках x1 = 3 и x2 = 1 функция имеет соответственно локальный минимум и локальный максимум. Поэтому надо найти значения функции в этих точках.

Е¨е область определения совпадает с областью определения самой функции. Поэтому она не имеет критических точек. А так как числитель дроби не равен нулю, то она не имеет и стационарных точек. В силу того, что в знаменателе многочлен неч¨етной степени, она больше нуля слева от вертикальной асимптоты и больше нуля справа от не¨. Поэтому график слева от асимптоты выпуклый вниз, а справа выпуклый вверх. Вс¨е это подтверждает правильность выводов, полученных с помощью пределов.

V. График не пересекает ось OX, так как числитель дроби, представляющей функцию, имеет отрицательный дискриминант. Ось OY пересекается в точке (0; '(0), то есть в точке (0; 2; 5). График не симметричен относительно координатных осей (См. Рис. 12.24).

23

12.3.4. Задача о наибольшем и наименьшем значениях функции, непрерывной на отрезке

Целью любого процесса, в котором участвует человек, является получение наибольшей прибыли при наименьших затратах1. Поэтому рассматриваемая в заголовке задача встречается достаточно часто. Но е¨ иногда путают с задачей отыскания локального экстремума, так как та задача

Y

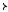X

3 2

2; 5

Рис. 12.24

является частным случаем этой. Идейная база задачи опирается на следующую теорему.

Теорема 12.15. О наибольшем и наименьшем значениях функции, непрерывной на отрезке Функция, непрерывная на отрезке, достигает на этом отрезке свои наибольшее и наименьшее значения, либо в стационарных или критических точках первой производной, либо на концах отрезка.

Данное утверждение является следствием теорем Вейерштрасса, Ферм´а

иусловий о наличии локального экстремума функции (теоремы 12.9-12.11).

Вотличие от многих теорем, которые являются только теоремами существования, данная теорема излагает алгоритм решения задачи. Пользуясь им, рассмотрим решение некоторых задач.

Задача 12.13. Найти наибольшее и наименьшее значение функции y = x3 3x + 4 на отрезке [0; 4].

Решение. Согласно теореме нам надо найти первую производную дан-

ной функции

y0 = 3x2 3:

Так как производная является многочленом, то она может иметь только стационарные точки. Приравняв производную к нулю, найд¨ем решение

уравнения

3(x2 1) = 0 , x = 1 или x = 1:

1Правда, во многих случаях сложно определить, что же на самом деле отнести к прибыли, а что

кзатратам. Но эта проблема выходит за рамки нашего курса.

24

Первая из точек не принадлежит заданному отрезку, поэтому оста¨ется рассмотреть значения функции в тр¨ех точках: одной стационарной x = 1

ина концах отрезка.

x = 0; y(0) = 4; x = 1; y(1) = 2; x = 4; y(4) = 56:

Следовательно, наименьшее значение на отрезке [0; 4] функция достигает в точке x = 1, и оно равно 2, а наибольшее значение она достигает в точке x = 4 и оно равно 56. С помощью символики это можно записать так:

min y(1) = 2; max y(4) = 56 .

x2[0;4] x2[0;4]

Задача 12.14. Найти наибольшее и наименьшее значение функции

p

g(x) = 3 (x 2)2 + 4 на отрезке [1; 3].

Решение. Как и в предыдущей задаче, вычислим производную

В этом случае производная функции g0 (x) не имеет стационарных точек, нигде не обращаясь в нуль, но имеет критическую точку x = 2, в которой она не определена, но которая принадлежит и области определения функции, и заданному отрезку.

Найд¨ем значения функции в этой точке, а также на концах отрезка.

x = 1; g(1) = 5; x = 2; g(2) = 4; x = 3; g(3) = 5:

Таким образом, наибольшее значение достигается на обоих концах отрезка, а наименьшее значение в критической точке первой производной.

Замечание 12.2. Следует обратить внимание, что в каждой из задач 12.13-12.14 не нужно исследовать знаки производной или значение второй производной для определения существования экстремума и его характера.

Рассмотрим две задачи с практическим содержанием, одна из которых попадает под формулировку теоремы, а вторая выходит за е¨ рамки.

Задача 12.15. Представьте, что вы получили прямоугольный участок земли для дачи с незакрепленной пока границей, а в придачу еще и штакетник для его ограды с известным периметром P . Какие размеры должен иметь ваш участок, чтобы его площадь была наибольшей?

Решение. Так как участок является прямоугольником, то, обозначив его длину за x, а ширину за y, получим площадь прямоугольника, как

25

функцию двух переменных

S(x; y) = xy:

Но так как периметр известен, то, связав переменные 2(x+y) = P , выразим одну из них через другую. Например, y = P2 x. Подставив представление y в формулу площади, получим новую задачу: Найти наибольшее значение

В результате вышепривед¨енных действий получен аналог задач 12.13- 12.14. Далее следуем по знакомому алгоритму.

Вычисляем значения в стационарной точке и на концах отрезка

Наибольшее значение данная функция, а следовательно, и площадь прямоугольника имеют в стационарной точке полученной функции, то есть при

x = P4 . Находим значение y = P2 P4 . То есть y = P4 . В результате получаем, что

Участок должен быть квадратом со сторонами, равными P4 .

1На самом деле, на практике ширина прямоугольника не может равняться ни нулю, ни его полупериметру. Но добавление концов отрезка упрощает решение задачи и не отражается на его практической стороне.

26

Задача 12.16. А теперь представьте, что вы получили прямоугольный участок земли для дачи с незакрепленной пока границей, площадь которого S, а вот о штакетнике вам прид¨еться подумать самим. А поскольку вы не миллионер, то желательно выяснить, при каких размерах участка его периметр будет наименьшим?

Решение. Так как участок по-прежнему является прямоугольником, то, в тех же обозначениях его периметр

P (x; y) = 2(x + y):

Но так как это функция двух переменных, то превратить е¨ в функцию одной переменной можно только с помощью уравнения связи S = xy, из

которого можно, выразив y = Sx , подставить его в функцию периметра

Но данную задачу уже нельзя решить как предыдущие, так как независимая переменная x пробегает не отрезок, а множество точек положительной оси. На этом множестве теорема не действует. Поэтому, если мы хотим получить решение задачи, то мы должны доказать, что на этом множестве функция имеет только одну стационарную точку первой производной, и что эта точка является точкой минимума функции. Тогда она же, в силу единственности, окажется и точкой, в которой функция достигает сво¨е наименьшее значение на всей положительной полуоси.

Найд¨ем производную

p

Поэтому в окрестности точки x = S производная меняет знак с минуса на плюс, то есть является точкой минимума, прич¨ем единственной на всей

положительной полуоси. Следовательно, в этой точке функция, а значит и p

периметр принимают наименьшее значение. Поскольку и y = S, то

27

p

Участок должен быть квадратом со сторонами, равными S .

Замечание 12.3. В заключение заметим, что в задаче 12.15 решение можно было найти без помощи производных, заметив, что функция

площади S(x) = P2 x x2 имеет своим графиком параболу с ветвями, направленными вниз. После этого можно было найти координаты вершины параболы, получив те же самые результаты. В задаче 12.16, чтобы обойтись без производной, нужно уже было обладать более глубокими знаниями из школьной программы. Демонстрация этих задач связана не со способом их решения, а с возможностью на элементарном уровне показать возможности дифференциального исчисления при решении так называемых задач минимакса. Далее мы обратимся к этой теме, но уже на уровне функций двух переменных.

28