tensor[2]

Внимание: энергия не инвариант, импульс тоже! W и S не являются компонентами

4-вектора, переход к (6.3) невозможен.

Как известно, энергия и импульс являются компонентами 4-вектора энергииимпульса. Значит, левые части уравнений непрерывности – тоже компоненты 4-вектора (который равен нулю).

иназывается тензором напряжений – название, идущее из механики сплошных сред.

Унас, конечно, никаких «напряжений» нет. И, к примеру, (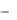 zx ) это количество z-й компо-

ненты импульса, протекающее через единичную площадку, перпендикулярную оси х, в единицу времени.

Из-за равноправия пространственных координат тензор напряжений симметричен, то есть, его компоненты не изменяются при перестановке индексов. Так что и весь тензор энер- гии-импульса симметричен, поэтому:

T 01 Sx / c , T 02 S y / c , T 03 Sz / c .

41

7. Волны и частицы

Будем рассматривать теперь монохроматические волны. Это означает, что в любой точке пространства поле (электрическое, магнитное, потенциал) является синусоидальной функцией времени: колеблется с определенной круговой частотой . Впрочем, мы допускаем, что волны имеют и другую физическую природу – к примеру, волны на воде, тогда с частотой 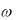колеблется соответствующая физическая величина.

Волновой 4-вектор

Нас интересует фаза 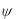колебания в каждой данной точке. Фазу мы рассматриваем

как полную, то есть, она может превышать 2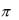(а иначе зависимость фазы от координат и времени будет разрывной – перешагнув 2 , фаза опять начнется с нуля). Поле фаз это скалярное поле, и можно записать его градиент:

x , y , z .

Как обычно, переходим в 4-пространство и находим 4-градиент:

Разбираемся с физическим смыслом полученного 4-вектора. Временная компонента содержит производную фазы по времени при фиксированных координатах; это не что иное, как круговая частота .

Пространственная компонента, градиент фазы, это (для фиксированного момента времени) вектор, направленный в сторону наиболее быстрого увеличения фазы. Учитывая,

что фаза на пути, равном длине волны , меняется на 2 , величина градиента равна 2 . В

физике это так называемый волновой вектор k. Точнее, волновой вектор это вектор, противоположный описанному: k 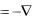, так как считают, что он должен показывать направление распространения волны. В то время как фаза возрастает, наоборот, против движения волны.

Теперь можно записать:

xi c , k .

Как любой градиент, это ковариантный вектор, можно перейти к контравариантному, поменяв знак у пространственной части. Окончательно:

pi Ec , p . Чтобы он полностью сделался таковым, нужно умножить (7.1) на коэффициент,

уравнивающий размерности:

42

43

Это формула изменения частоты при переходе к системе отсчета, движущейся относительно первоначальной со скоростью v – формула эффекта Доплера. Разумеется, та же самая формула действительна для энергии кванта:

некоторыми коэффициентами), то в данном случае k i ki 0 . Вспоминая, что волновой вектор это градиент фазы, получаем:

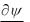
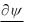0 . xi xi

Это так называемое уравнение эйконала, применяемое в геометрической оптике, а фа-

за 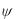это эйконал.

Волны де Бройля

Допустим теперь, что m 0 . Из (7.3) сразу следует, что v c . Точнее, из (7.4):

Это волны де Бройля, связанные с массивной частицей. Фазовая скорость волн де Бройля сверхсветовая. Конечно, здесь нет ничего, противоречащего теории относительности: ведь фазовая скорость – это скорость перемещения нематериального, математического объекта (геометрического места точек постоянной фазы).

А вот скорость переноса энергии (групповая скорость) вполне досветовая. Формула для групповой скорости:

Подставляем: k 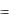p , 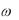E , и получаем:

dE vgr dp .

Для нерелятивистской частицы возьмем школьные формулы кинетической энергии

mv 2 и импульса mv . Получится vgr v , т. е. групповая скорость волны де Бройля равна

2

скорости частицы.

44