Контрольные вопросы

1. Какие методы решения систем линейных алгебраических уравнений являются прямыми? Чем они характеризуются?

2. Каково условие существования и единственности решения системы уравнений?

3. Какие методы называются итерационными? В чем их отличие от прямых?

4. Какой метод обеспечивает более быструю сходимость – метод простых итераций или Зейделя?

5. В чем состоит отличие метода Зейделя от метода простых итераций?

6. Для каких порядков систем применяются прямые и итерационные методы?

7. Для чего применяется модифицированный метод Гаусса – метод Гаусса с выбором наибольшего элемента по столбцам?

Лабораторная работа 2 решение нелинейных уравнений

Цель и задачи работы: изучение методов решения нелинейных уравнений и систем, приобретение навыков их практического использования.

Решение алгебраических уравнений методом половинного деления

Пусть - некоторое уравнение. Числоназывается корнем (нулем) уравнения, если оно, будучи подставлено в уравнение, обращает его в равенство. Функциянепрерывна на отрезкеи.

1. Находится середина отрезка :

.

2. Если , то для продолжения вычислений выбирается та из частей данного отрезка, на концах которой функция имеет разные знаки:

если , то;

если , то.

3. Вычисляется погрешность данного шага:

.

Если погрешность превышает заданное значение , вычисления повторяются с первого шага до тех пор, пока выполняется условие. Когда погрешность вычислений на данном шаге становится меньше заданного значения, считается, что кореньуравнения найден с погрешностью, не превышающей .

Метод отделения корней

Метод отделения корней используется для определения интервалов, в которых содержатся корни уравнения. Это может быть сделано тремя способами.

1. Вычисляются значения функции в нескольких точках отрезка и строится таблица. Если в двух соседних точках 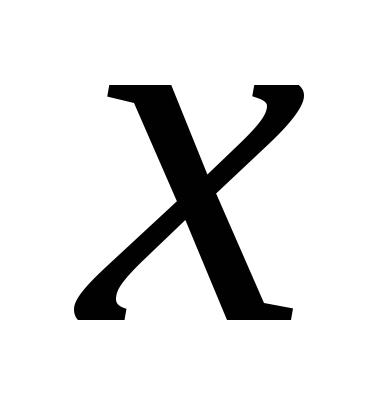функция имеет разные знаки, то корень уравнения находится между этими точками.

2. Строится график функции и находятся точки пересечения его с осью абсцисс.

3. Исходная функция представляется в эквивалентном виде . Строятся графики этих функций и находятся точки пересечения этих графиков.

На рис. 2.1 представлено окно программы, реализующей метод отделения корней тремя способами. Исходное уравнение .

Рис. 2.1. Три способа отделения корней

1. Находя последовательно значения функции для всех целых на отрезке и проверяя знак функции, выделим два отрезка, на которых функция меняет знак: и (рис. 2.1, вверху справа).

2. Строится график функции 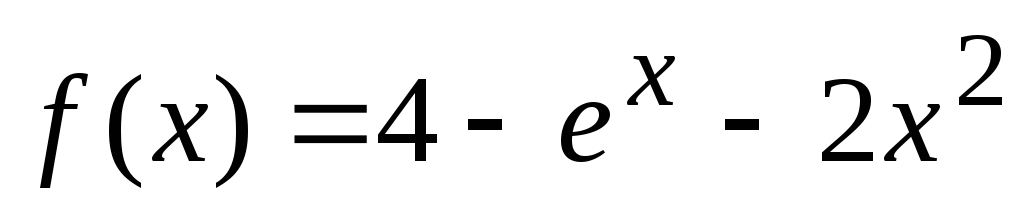и находятся точки его пересечения с осью абсцисс либо отрезки, содержащие точки пересечения.

3. Строятся графики функций ии находятся точки их пересечения.

Метод итераций

Метод итераций заключается в последовательном приближении к решению , которое может быть найдено с заданной точностью. При решении методом итераций исходное уравнениепреобразуется к эквивалентному:

, ,.

Отсюда .

Произвольным образом выбирается начальное приближение , которое подставляется в правую часть уравнения. Повторяя этот процесс, получим последовательность чисел, где.

Итерационный процесс сходится, если выполняется условие при.

Для достижения требуемой точности итерационная формула применяется многократно до тех пор, пока соблюдается условие.