
2360
.pdfМинистерство образования и науки Республики Татарстан Альметьевский государственный нефтяной институт
|
|
|
|
|
|
А.Ф. Иванов |
|
|
|
А |
Г |
||
|
|
|
|
|
|
|
|
|
|
т е |
ка |
|
|
|
|
|
|
Программирование и основы |
|
||||||||
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
алгоритмизации |
|
|
|
|||||
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|
Методические указан я |
|
|
|
|
||||
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
по выполнению лабораторныхи |
работ |
|
|
|
||||
|
|
|
|
и по организации и проведению самостоятельной работы |
|
||||||||
|
|
|
|
для студентов, обучающ хся по специальности 220301 |
|
||||||||
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
«Автоматизация технолог ческ х процессов и производств» |
||||||||||
|
|
|
|
|
очной и очно-заочнойи |
форм обучения |
|
|
|
||||
|
|
е |
к |
т |
ронная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
л |
|
|
|
|
|
|
|
|
|
|
||
Э |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Альметьевск 2009 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
НИ
|
УДК 683.1 |
|
|
|
|
|
|
|
|
|
НИ |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
И 20 |
|
|
|
|
|
|
|
|
|
|
|
И 20 |
Иванов А.Ф. |
|
|
|
|
|
|
|
|
Г |
|
|
Программирование |
и |
основы |
алгоритмизации. |
Методические |
||||||||
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
указания по выполнению лабораторных работ и по организации и |
|||||||||||
|
проведению самостоятельной работы для студентов, обучающихся по |
|||||||||||
|
специальности 220301 «Автоматизация технологических |
процессов и |
||||||||||
|
|
|
|
|
|
|
|
|
ка |
|
|
|
|
производств» очной и очно-заочной форм обучения – Альметьевск: |
|||||||||||
|
Альметьевский государственный нефтяной институт, 2009. – 36 с. |
|||||||||||
В |
методических |
указаниях |
приводится |
|
е |
|
|
материал, |
||||
|
т ор тический |
|||||||||||
необходимый |
для выполнения |
лабораторных |
работ, приведены |
|
примеры, |
|||||||
|
|
|
|
|
|
|
о |
|
|
|
|
|
контрольные вопросы и задания для отработки навыков составления программ. |
||||||||||||
Учебное |
пособие |
предназначено для |
и |
|
|
|
|
|
|
|||
п дгтт вки дипломированных |
||||||||||||
специалистов по направлению 220301.65 «Автоматизированные технологии и |
|||||||||
производства». |
|
|
|
б |
л |
||||
|
|
|
|
||||||
|
|
|
|
|
|
|
и |
|
|
|
Печатается по решению учебно-метод ческого совета АГНИ. |
||||||||
|
|
|
|
|
ронная |
б |
|
|
|
|
|
Рецензенты: доцент кафедры информатики, к.п.н. Садриева Л.М. |
|||||||
|
|
|
|
|
доцент к федры ВМ, к.п.н. Зарипова З.Ф. |
||||
|
|
е |
к |
т |
|
|
|
|
|
|
л |
|
|
|
|
|
|
||
Э |
|
|
|
|
|
|
© Альметьевский государственный |
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
нефтяной институт, 2009 |
|
|
|
|
|
|
|
|
2 |
|

Разработка алгоритмов линейной структуры
Лабораторная работа
Разработка алгоритмов линейной структуры
Цель работы. |
|
|
Приобретение навыков составления алгоритмов линейной структурыНИ. |
||
Теоретическая часть. |
|
Г |
Под алгоритмом понимают описание |
последовательности действий, |
|
|
А |
|
строгое исполнение которых приводит к решению пост вленной задачи за
конечное число шагов.
т |
|
: |
Любой алгоритм должен обладать следующими свойствамика |
||
– определенность − неизбежность получения одногое |
и того же результата |
|
при многократном применении алгоритма к одним и тем же исходным данным;
|
|
|
|
л |
которое предполагает, что |
– результативность − это свойство алгоритмао, |
|||||
|
|
|
б |
|
определенных результатов |
выполнение алгоритмов завершаются по учениеми |
|||||
через конечное число шагов; |
|
и |
|
|
|
|
|
|
|
|
|
– массовость − возможность применения алгоритма для решения класса |
|||||
|
б |
|
|
|
|
задач, отличающихся лишь исходными данными. |
|
||||
ронная |
|
|
|
|
|
Для проверки работоспособности алгоритма необходимо задать значения входных переменных, вычислить конечный результат по алгоритму и сравнить с результатом ручного счета.
Простейшие задачи имеют линейный алгоритм решения. Линейный алгоритм представляет собой набор команд, выполняемых последовательно друг за другом, при эт м все блоки алгоритма располагаются друг под другом в определённой последовательности, согласно условию задачи. В линейных
алгоритмах о су ствуют блоки проверок условий и повторений и присутствуют
блоки ввода и вывода, а также арифметические блоки. На практике линейные |
|||||||||||
алгоритмык |
т |
|
|
|
|
|
|
|
|||
встречаются редко, например, при расчёте громоздких формул. |
|||||||||||
|
|
Схематично линейный алгоритм можно представить следующим образом: |
|||||||||
|
Э |
л |
е |
|
|
|
|
|
|
|
|
|
Действие 1 |
|
Действие 2 |
|
… |
|
Действие N |
|
|||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
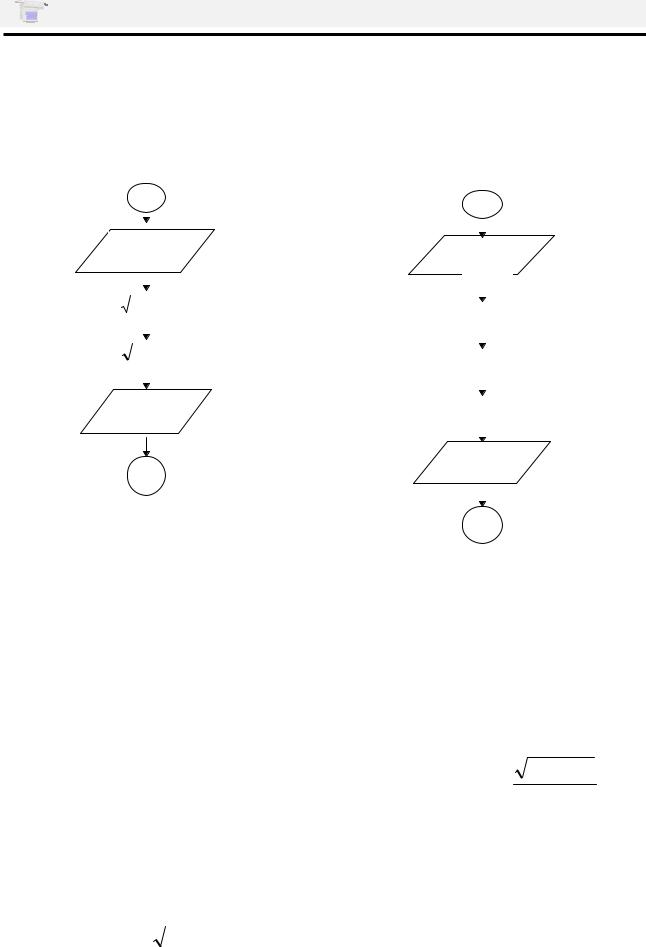
Разработка алгоритмов линейной структуры
Пример 1. |
|
|
|
|
|
|
|
Пример 2. |
|
|
|
|
|
|
НИ |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Даны четыре натуральных числа. |
Даны действительные числа a и b. |
|||||||||||||||||||
Найти квадратные корни суммы |
и |
Найти x=y+z, где y=a+b, z=5y+11ab. |
||||||||||||||||||
произведения этих чисел. |
|
|
|
|
|
|
|
|
|
|
|
Г |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Н |
|
|
|
|
|
|
|
|
Н |
А |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a,b,c,d |
|
|
|
|
|
|
|
|
ка |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a, b |
|
|
||
|
S = |
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
a + b + c + d |
|
|
|
|
|
|
|
|
|
|
y=a+b |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P = |
|
a× b×c×d |
|
|
|
|
|
|
|
о |
|
|
z=5y+11ab |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
S,P |
|
|
л |
|
|
|
x=y+z |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
К |
|
б |
|
|
|
|
|
x,y,z |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1.Дан радиусроннаякруга. Найти площадь круга.
2.Найдите высоту и объем конуса, если известны длина образующей конуса и радиус основа ия.
3.Даны 5 натураль ых чисел. Найти квадратные корни суммы и произведе ия этих чисел. 16тЗадания к лабораторной работе:
|
|
арифметическими операциями кроме умножения, получить а |
за четыре |
||||||||||||||||
|
|
|
к |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
л |
операции. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
х, |
у, z. |
Вычислить |
|
значения |
a и b: |
||||||
|
6. Даны числа |
|
|
|
|
||||||||||||||
Э |
|
е |
|
|
|
|
|
|
æ |
2x ö |
|
4y 2x + y + z |
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
a |
= cos |
(y - 3 |
x |
|
ç3z + |
|
÷, b |
= x + |
|
+ |
|
|
|
. |
|
|||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
è |
3 ø |
4 |
23 |
|
|
12 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
Разработка алгоритмов линейной структуры |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Контрольные вопросы: |
|
|
|
|
|
|
|
|
|
НИ |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
1. |
Назовите этапы подготовки и решения задач на ЭВМ. |
|
|
|
|||||||||
|
|
|
|
2. |
Что такое алгоритм? |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
3. |
Укажите способы описания алгоритмов. |
|
|
|
А |
Г |
|
||||||
|
|
|
|
4. |
Какими свойствами должен обладать алгоритм? |
|
|
||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
5. |
Какие алгоритмы называется линейными? |
|
|
|
|
|
|
||||||
1. |
Даны три числа: a, b, c. Найти сумму и произведение данных чисел. |
||||||||||||||||
2. |
Даны основания и высота трапеции. Получить п риметр и площадь. |
||||||||||||||||
3. |
|
|
|
|
|
|
|
|
|
ка |
|
|
|
||||
Дано ребро куба. Найти объем куба и его полную пов рхность. |
|
|
|||||||||||||||
4. |
|
|
|
|
|
|
|
|
е |
|
|
|
|
||||
Даны катеты прямоугольного треугольника. Най и гипотенузу и площадь |
|||||||||||||||||
|
|
|
|
треугольника. |
|
|
|
|
т |
|
|
|
|
|
|||
5. |
Даны стороны прямоугольника. Найти д агональо , периметр и площадь |
||||||||||||||||
|
|
|
|
этой фигуры. |
|
|
|
и |
|
|
|
|
|
|
|||
6. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Задан радиус. Вычислить диаметр круга, длину окружности, площадь |
|||||||||||||||||
|
|
|
|
круга. |
|
и |
б |
л |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
8. |
Дано действительное число |
a. Не пользуясь никакими другими |
|||||||||||||||
|
|||||||||||||||||
|
|
|
|
арифметическими операци миб |
кроме умножения, получить а21 за шесть |
||||||||||||
|
|
|
|
операций. |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
е |
к |
ронная |
|
|
|
|
|
|
|
|
|
|
|
Э |
л |
|
5 |
||
|

Разработка алгоритмов ветвящейся структуры
Лабораторная работа
Разработка алгоритмов ветвящейся структуры
Цель работы. |
|
|
Приобретение навыков составления алгоритмов ветвящейся структурыНИ. |
||
Теоретическая часть. |
|
Г |
Алгоритм является ветвящейся структуры (ветвление) если |
выбранный |
|
|
А |
|
метод решения задачи предполагает выполнение р зличных действий в
зависимости от значений каких-либо исходных или промежуточных |
|||||||||||||||||||||||
переменных, но при этом каждая ветвь алгоритма в процкассе решения задачи |
|||||||||||||||||||||||
проходится не более одного раза. |
|
|
|
|
|
|
и |
о |
|
т |
е |
|
|
|
|
|
|
||||||
|
Разновидности ветвящихся алгоритмов: |
|
|
|
|
|
|
|
|
||||||||||||||
|
• |
ответвление |
|
|
|
|
л |
|
|
|
|
|
|
|
|
|
|||||||
|
• |
разделение |
|
|
б |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
• |
выбор. |
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
структуры необходимо |
|||||||
|
При тестировании алгоритмов ветвящейся |
||||||||||||||||||||||
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
Н |
|||||
подбирать такие исходные данные, что ы можно было проверить все ветви. |
|||||||||||||||||||||||
Пример 1. |
|
ронная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a, b |
|||||||||
Даны числа а, b. Найти р зность между |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
большим и меньшим. |
|
|
|
|
|
|
|
да |
|
|
|
|
|
|
|
нет |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
a<b |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к |
|
|
|
|
|
|
|
S=b-a |
|
|
|
|
|
|
S=a-b |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
л |
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
||||||||
Э |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
К |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
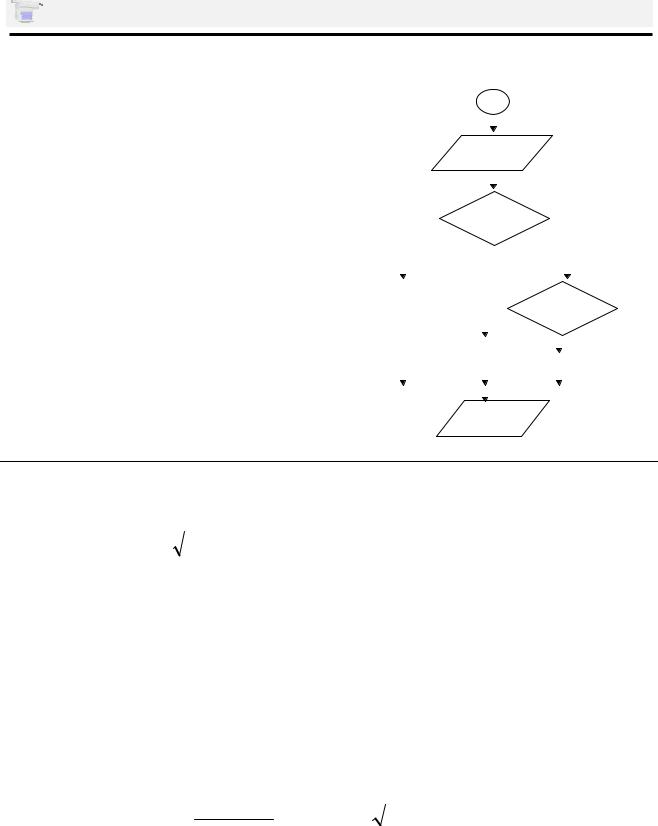
Разработка алгоритмов ветвящейся структуры
|
Пример 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Н |
|
|
|
|
|
НИ |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||||||||
|
Для данного вещественного числа х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
вычислить значение функции у: |
|
|
|
|
|
|
|
да |
|
|
|
|
|
|
|
|
|
|
нет |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
ì5x - 3, если x ³ 5, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x³5 |
А |
|
Г |
|
|||||||||
|
ï |
|
|
если -1£ x < 5, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
y = í3x, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ка |
|
|
|
|
|||||||||
|
ï |
2 |
, |
если x < -1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
îx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y=5x-3 |
|
е |
нет |
|
|
x<-1 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
y=3x |
|
|
|
|
|
да |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
y=x2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
|
y |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
3 |
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Задания к лабораторной работе: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Составьте алгоритм решения задачи: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1. |
Вычислить: x- |
1- 0,3x |
|
для данного числа х. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
б |
|
|
|
ì12x + 43, |
|
|
если х ³ 30; |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Составить алгоритм решения задачи. Даны вещественные числа а, в, с. Удвоить эти числа, если а³в³с, и заменить их модулем, если это не так.
|
4. Запишите алг ритм нахождения числа корней уравнения х2=а+1 в |
||||
|
|
зависим сти т значения а. |
|||
|
|
т ронная |
|
|
|
|
|
|
|
|
|
|
|
к |
|||
|
|
е |
|||
|
|
если данные функции вычислить невозможно, сделать об этом |
|||
|
л |
сообщение. |
|||
Э |
6. Даны целые числа k, l. Если числа не равны, то заменить каждое из них |
||||
одним и тем же числом, равным большему из исходных, а если равны, то заменить числа нулями.
7

Разработка алгоритмов ветвящейся структуры
Э
7. |
Вычислить |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
НИ |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Контрольные |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Г |
|
||||||
|
1. |
Как ветвление обозначается в блок-схемах? |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
2. |
Какие разновидности ветвления Вы знаете? Приведите примеры. |
||||||||||||||||||||||||||
|
3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
Чем отличаются разновидности ветвящихся алгоритмов: ответвление и |
|||||||||||||||||||||||||||
|
|
разделение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ка |
|
|
|
|
|||||
|
Задания |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Составьте |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1. |
Вычислить |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
т |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2. |
Вычислить |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
y |
|
|
|
|
л |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 3, |
если х ³ 0; |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ìx |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ï |
|
и |
|
|
|
|
|
|
|
|
3. Для данного числа х вычислить у: у = í1 |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
ï |
|
, |
|
если х < 0. |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
îx |
|
|
|
|
|
|
|
|
|
|
4. Даны числа а, в, с. Найти разность между большим и меньшим. |
|
|||||||||||||||||||||||||||
5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
большего из трех чисел а, в, с и |
||||||||||
Составить программу определен я |
||||||||||||||||||||||||||||
|
вывести на экран квадратный кореньи |
большего числа. |
|
|
|
|
||||||||||||||||||||||
6. |
|
|
|
|
ронная |
|
|
|
|
определяющее возраст человека (в |
||||||||||||||||||
Дано натуральное число n(n≤100), |
||||||||||||||||||||||||||||
|
годах). Дать для этого числа наименование " год ", " года " или " лет ": |
|||||||||||||||||||||||||||
|
например, один год, 23 года, 45 лет и т.д. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
7. |
Вычислить y, для д нного числа х: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
у=х2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||||||
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-4 -2 |
|
|
X |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
к |
|
-1 |
|
|
1 |
|
|
|
|
X |
|
|
|
|
|
-2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-3 |
|
|
|
|
|
|
а) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
8. |
Даны три вещественных числа. Удвоить из них те, которые принадлежат |
||||||||
|
интервалу [1;3]. |
|
|
|
|
|
|||
9. |
Вычислить: |
3х + 2sin7 x |
|
|
|
|
, если х - дано. |
||
|
|
|
x+2 |
||||||
|
|
|
|
|
|
||||
л |
|
2 x4 +1 |
− |
ln x −1 |
+ 4 |
|
|
||
|
|
8 |
|
|
|
||||
|
|
|
|
|
|
|
|
||

|
|
|
|
Разработка алгоритмов циклической структуры |
|
|
|
|
|
|
|
|
|
Лабораторная работа |
|
|
|
|
|
|
|
|
Разработка алгоритмов циклической структуры |
|
|
|
|
Цель работы. |
|
|
|
|
Приобретение навыков составления алгоритмов циклической структурыНИ. |
|
|
|
|
Теоретическая часть. |
Г |
|
|
Алгоритмы циклической |
структуры |
(повторение) – алгоритмы, в |
|||||||||||||||||||||
которых отдельные действия выполняются многократно. |
А |
||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|
Количество повторений цикла должно быть полностью определено |
|||||||||||||||||||||||
алгоритмом решения задачи, иначе возникает явл ние «казацикливания», при |
|||||||||||||||||||||||||
котором процесс решения задачи не может заверши ьсяе. |
|
||||||||||||||||||||||||
|
|
Тело цикла – многократно повторяющиеся действият |
алгоритма. |
||||||||||||||||||||||
|
|
Параметр цикла – величина, с изменением которойо |
связано многократное |
||||||||||||||||||||||
выполнение цикла. |
|
|
|
|
|
|
и |
|
|||||||||||||||||
|
|
Разновидности циклических алгоритмов: |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
л |
|
|
|
|
|
• цикл с заранее известным ч слом повторений: |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
цикл С ПОСТУСЛОВИЕМ и цикл С ПРЕДУСЛОВИЕМ |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
• цикл с заранее неизвестным числом повторений |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
Пример 1. Найти сумму натуральных чисел не превосходящих 500. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
н |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
S=0 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
ронная |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
да |
|
|
|
|
нет |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
к |
т |
|
|
|
i>500 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s=s+i |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На рисунке показана |
|
|
|
|
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Вывод S |
|
|
|
|
|
|
|
|
|
|
i=i+1 |
|
|
|
блок-схема организации |
|||||||
Э |
л |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
цикла с предусловием. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
к
9

|
|
|
|
|
|
|
|
|
Разработка алгоритмов циклической структуры |
||||||||||||||||
Пример 2. |
|
|
Н |
|
|
|
|
|
|
|
|
|
|
Пример 3. |
|
|
|
|
|
НИ |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Найти сумму чётных натуральных |
|
Найти наименьшее число n при котором |
|||||||||||||||||||||||
чисел не превосходящих 150. |
|
|
|
|
сумма S=1+1/2+1/3+1/4+1/5+….+1/n |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
превысит 2,5. |
|
|
|
|
Г |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
н |
А |
|
|
|
|
|
|
S=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ка |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
i=2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S=S+i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S=S+1/n |
|
|
|
||
|
|
|
|
i=i+2 |
|
|
|
|
|
|
|
|
|
|
|
|
и |
о |
|
е |
|
|
|
|
|
|
|
нет |
|
|
|
|
да |
|
|
|
|
|
|
|
|
л |
|
n=n+1 |
|
|
|
||||
|
|
|
i≤150 |
|
|
|
|
|
|
|
|
|
_ |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
+ |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S >2,5 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
S |
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|||
|
|
К |
|
|
|
|
|
|
|
|
|
б |
|
|
|
|
Вывод n |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
ронная1 1 1 1 |
|
1 |
|
|
|
|
|
|
|
к |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
На рисунке показана блок-схема |
|
На рисунке показана блок-схема |
|
||||||||||||||||||||||
организации цикла с постусловием. |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
организации цикла с заранее |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
неизвестным числом повторений. |
|
||||||||||
|
Задания к лаборатор |
ой работе: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Составьте алгоритм решения задачи: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
1. |
Вычислить: 1,1+1,2+1,3+…+190,3. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
2. |
Для данного числа а вычислить: a + a2 |
+ a3 |
+ a4 |
+ ... + a20 . |
|
|
|
|||||||||||||||||
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
4 |
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
3. |
Вычисли ь: |
− |
|
+ |
|
− |
|
+ ... − . |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
е |
|
|
100 |
|
98 |
|
96 |
|
94 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
4. |
Вычислитьк |
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Э |
л |
cos1 − cos1+ cos2 |
+ cos1+ cos2 |
+ cos3 − ... + cos1+ cos2 + cos3 + ... + cos101. |
|||||||||||||||||||||
|
sin1 |
sin1+ sin 2 |
|
sin1+ sin 2 |
+ sin3 |
|
|
sin1 + sin 2 + sin 3 + ... + sin101 |
|||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
|
|
|
|
