Пассивные колебательные системы

В цепи, содержащей индуктивность и емкость, могут возникать электрические колебания. Поэтому такая цепь называется колебательным контуром. По отношению к внешней цепи он может быть включен так, как показано на рис.4.1а), тогда он называется – параллельный контур, либо так,

r

А) l r c а) l r c б)

Рис.4.1. Колебательный контур. а)- параллельный; б)- последовательный.

как показано на рис.4.1б) – последовательный контур. Резистор r, последовательный с индуктивностью, - сопротивление проволоки катушки L.

Влияние этих схем на внешнюю цепь неодинаково, поэтому рассмотрим их по отдельности.

ЛАБОРАТОРНАЯ РАБОТА №4. Параллельный колебательный контур

U_вх

U_вых

R,100к

C, 0.01

L, 8мГн

r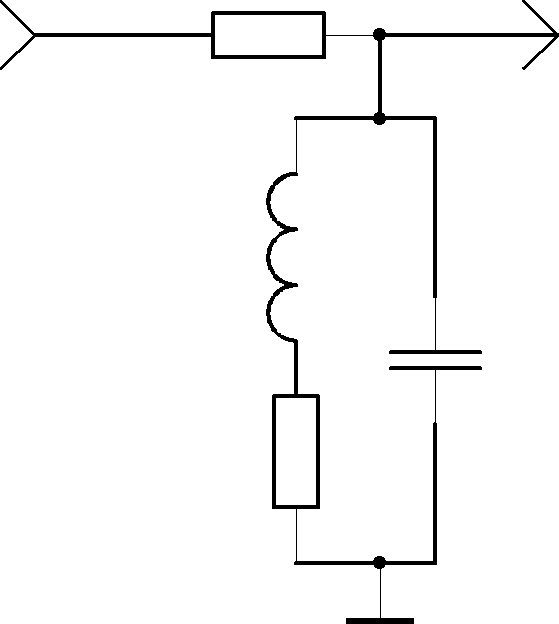

Рис.4.2. Схема исследования параллельного контура.

Для схемы (рис.4.2):

• Передаточная функция

A(j)= U_вых / U_вх = (4.1)

• Коэффициент передачи по напряжению определяем согласно (1) и получим

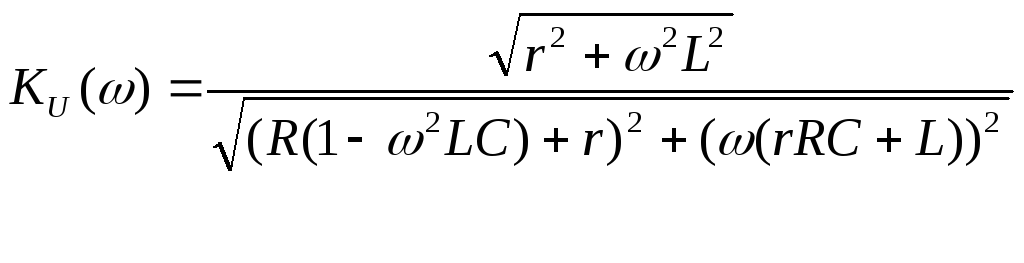
(4.2)

Из (4.2) видно, что в области малых частот коэффициент передачи К_U=r/(r+R), а при неограниченном увеличении частоты – стремится к нулю.

Частота, для которой выполняется условие, или

(4.3)

называется собственной (резонансной) частотой колебательного контура и является одной из его основных характеристик. Импеданс контура на резонансной частоте , а его модульили при большихQ – . Здесь - волновое сопротивление, а- добротность, также важные характеристики колебательного контура.

, а(4.4)

Волновое сопротивление связывает амплитудное значения напряжения на контуре с током в его ветвях , а добротность характеризует резонансные свойства контура: чем выше добротность, тем меньше потери энергии в контуре и слабее затухают свободные колебания в нем.

Коэффициент передачи схемы (рис.4.2) на резонансной частоте

K_U() = (4.5)

или

К_U() = 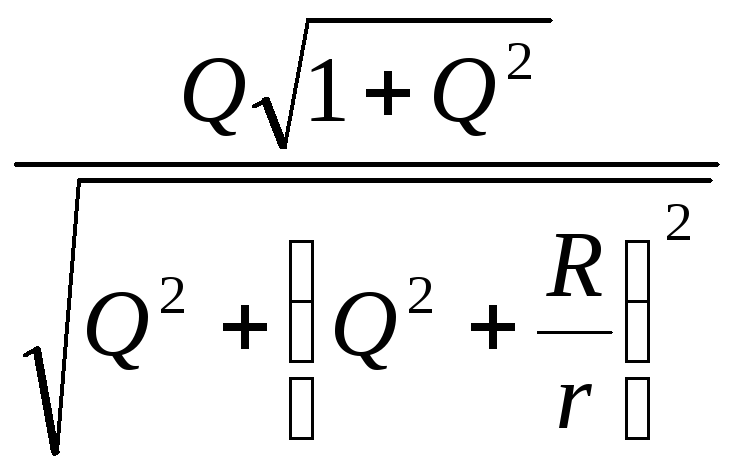(4.6)

И при условии

R/r <<Q² , К_U() 1

• Переходную характеристику h(t) аналитически получить достаточно сложно и мы отложим этот вопрос до практической части работы.

Порядок выполнения работы.

1. Соберите схему (4.2). По формуле (4.3) оцените резонансную частоту контура .

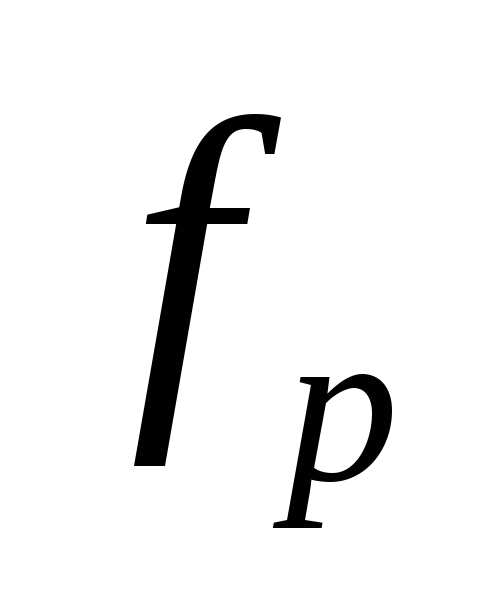2. К выходу схемы подключите осциллограф, подайте на вход схемы гармонический сигнал от генератора и, меняя частоту, по максимальному значению амплитуды выходного напряжения U_max определите точное значение 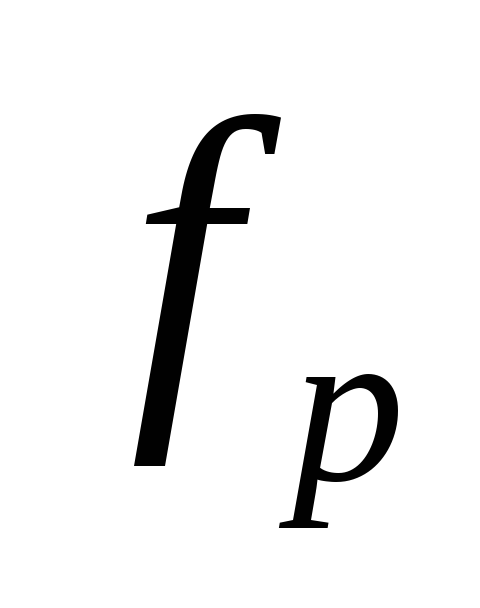и сравните с вычисленным значением. Уточните значение индуктивности катушки. В интервале частот 1кГц – 100кГц, измеряя осциллографом выходное напряжение, постройте по экспериментальным значениям зависимость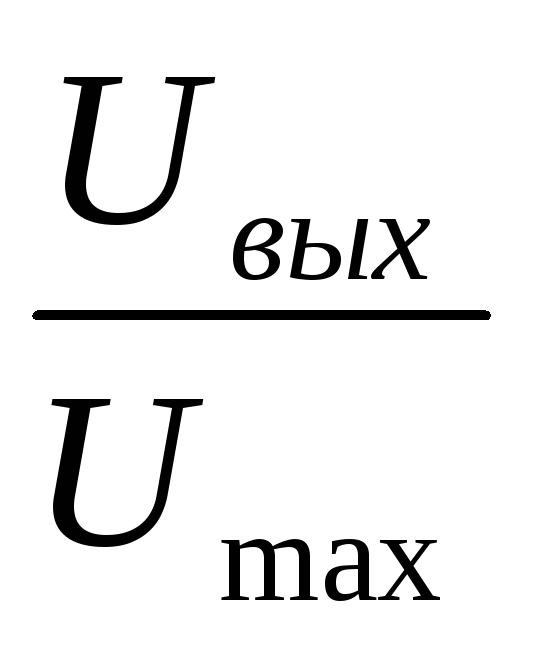=f(lg(f/f₀)), f₀ = 10Гц.

3. На уровне 0,707 определите полосу частот =f_в – f_н (рис.4.3) и, по

формуле определите добротность контура.

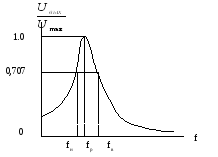
Рис.4.3. Примерный вид резонансной кривой контура.

4. По значению добротности и уточненного значения индуктивности

и выражению (4.4) найдите значение r и сравните его с измеренным напрямую омметром. Объясните результат.

5. Вычислите волновое сопротивление контура.

6. Подайте на вход схемы последовательность прямоугольных импульсов с частотой , много меньшей резонансной, чтобы на экране осциллографа была картина свободных затухающих колебаний в контуре U(t) = U₀e ^-t cos(t + ). Это и будет переходная характеристика. Определите частоту этих колебаний и сравните сf_р (п.3) и (4.3), а изображение представьте в отчете.

ЛАБОРАТОРНАЯ РАБОТА №5. Последовательный контур

Для исследования четырехполюсника с последовательным контуром надо собрать схему (рис.5.1).

R, 1к

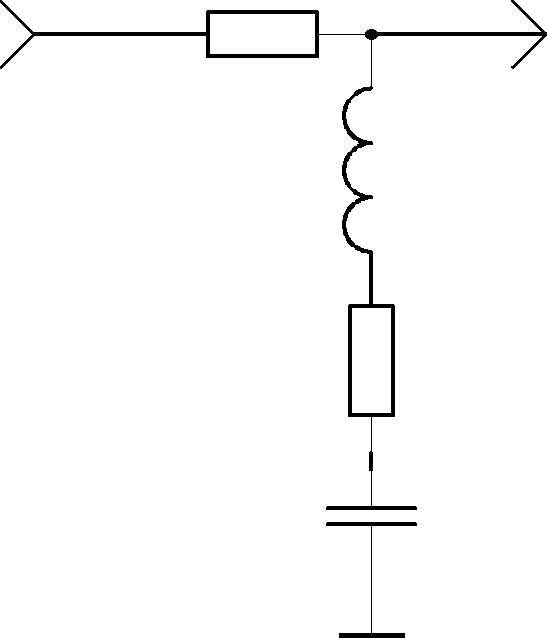
L,8мГн

r

С, 0,01

Рис.5.1. Схема исследования последовательного контура.

Для этой схемы:

• Передаточная функция

A(j)= U_вых / U_вх = 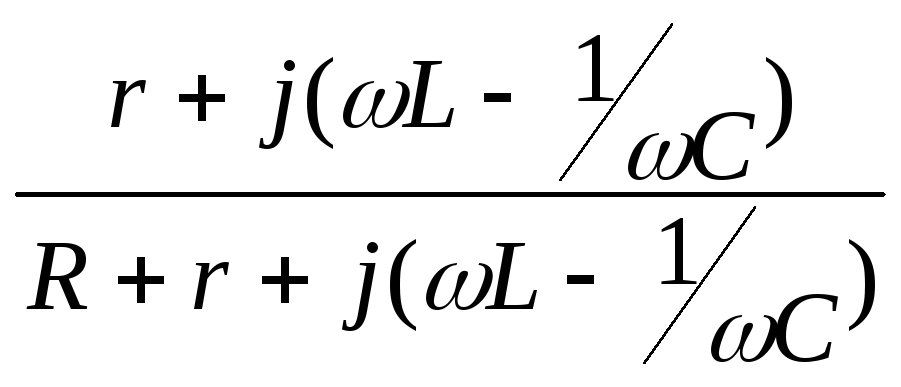(5.1)

• Коэффициент передачи по напряжению определяем согласно (1) и получим

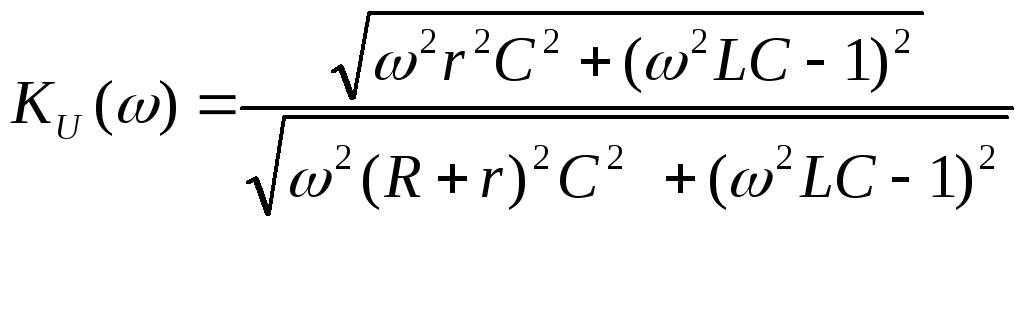
(5.2)

Из (5.2) видно, что в области малых частот и при неограниченном увеличении частоты - коэффициент передачи стремится к единице, а на резонансной частоте , где по- прежнему

(5.3)

называется собственной (резонансной) частотой колебательного контура и является одной из его основных характеристик, так же как - волновое сопротивление и- добротность колебательного контура.

, а(5.4)

Волновое сопротивление связывает амплитудные значения на контуре с током в его ветвях , а добротность характеризует резонансные свойства контура: чем выше добротность, тем меньше потери энергии в контуре и слабее затухают свободные колебания в нем.

Порядок выполнения работы.

1. Соберите схему (5.1).

2. По формуле (5.3) оцените резонансную частоту контура .

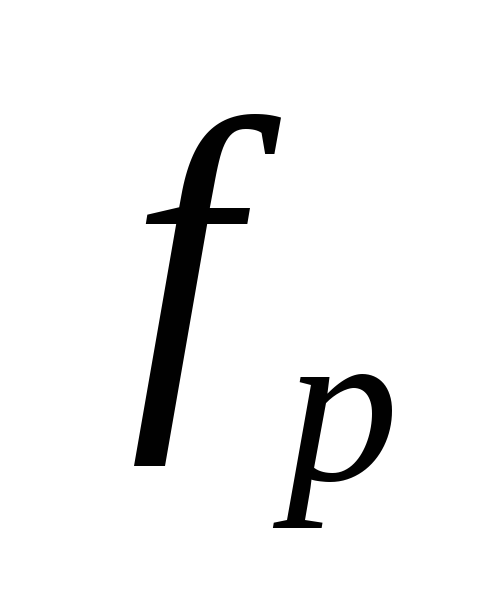3. К выходу схемы подключите осциллограф, подайте на вход схемы гармонический сигнал от генератора и, меняя частоту, по минимальному значению амплитуды выходного напряжения U_min определите точное значение 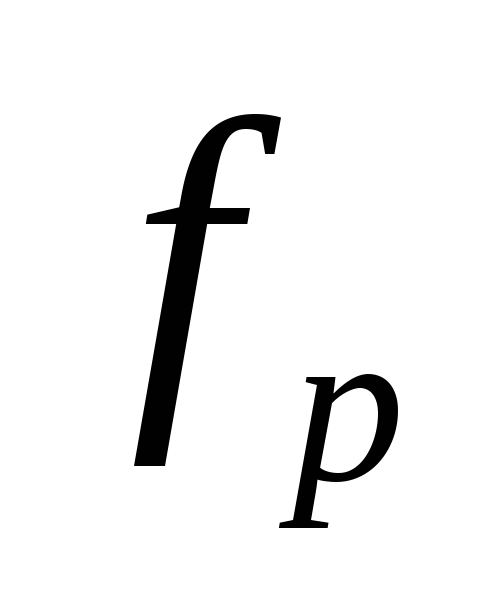и сравните с вычисленным значением. Уточните значение индуктивности катушки.

4. В интервале частот 20Гц – 100кГц, измеряя осциллографом входное и выходное напряжение, постройте по экспериментальным значениям зависимость К_u(f) = K(lg(f/f₀)), f₀ = 10Гц.

5. Проанализируйте поведение АЧХ и подумайте, как определить добротность контура.

6. По значению добротности и уточненного значения индуктивности и выражению (4.4) найдите значение r и сравните его с измеренным напрямую омметром. Объясните результат.

7. Опишите признаки резонанса напряжений.