2.2. Расчет коэффициента периодичности для двух случаев выполнения пересечений включений в ячейке квазипериодичности

I. Случай больших объемных долей.

Если величина вектора смещений а при больших объемных долях включений будет меньше или равна толщине включения ∆h , то при всех случайных значениях смещений ∆ будут наблюдаться всегда пересечения включений, отсюда следует (используем (1) и (2)), что , тогда; (5)

Учитывая, что , разделим получившееся неравенство (5) на высоту ячейки квазипериодичности H.

Получим следующее выражение:

, следовательно

. (6)

При условии (6) , среднее значение площади пересечения включений будет равно:

.

Найдем V₁₁: 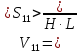, тогда

, т.к. ∆ известна и находится по формуле (1.1) , то подставив эту величину в выражение для V₁₁ и сгруппировав, получим:

(7)

Получившееся выражение (7) для V₁₁ подставим в формулу (3) для коэффициента периодичности p :

.

II. Случай малых объёмных долей.

Аналогично рассмотрим случай малых объемных долей, когда пересечения включений могут не наблюдаться, т.е. случай, когда вектор смещений включений больше толщины самого включения ∆ > h.

Тогда (8)

Из формулы (4.1) для осредненного значения площади пересечения включений получим:

,

решая интеграл, и подставив формулу (1.1) получим, что

.

НайдемV₁₁ :

.

Упростим полученное выражение, разделив правую часть на H². Окончательный результат относительного объемного содержания пересечения включений в ячейке равен:

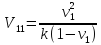. (9)

Находим формулу для коэффициента периодичности р, подставляя все необходимые результаты в выражение (3)

.

2.3. Результат расчета и построение графика коэффициента периодичности

Рассмотрев два случая, малых и больших объемных долей включений, результат вычисления коэффициента периодичности определяется следующим выражением:

График зависимости коэффициента периодичности p композита с ориентированными пластинчатыми включениями от относительного объемного содержания включений для разных значений степени разупорядоченности показан на рис. 5:

p

v₁

Рис.5. Коэффициент периодичности для степени разупорядоченности k = 1(1), k = 2/3 (2), k = 1/3 (3).