6.Исследование функции на овражность

Постановка задачи:

Требуется исследовать на овражность функцию :

Теоретические сведения:

Определение 6.1

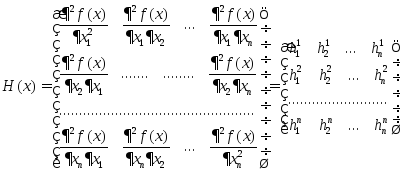
Матрицей Гессе дважды дифференцируемой в точкефункцииназывается матрица частных

производных второго порядка, вычисляемых в данной точке:

Определение 6.2

Собственные значения матрицыразмеранаходятся как корни

характеристического уравнения (алгебраического уравнения n-й степени):

Определение 6.3

Пусть ограниченная снизу функция:

обладает той особенностью, что в исследуемой области собственные значения матрицы Гессе , упорядоченные

в любой точке , удовлетворяют неравенствам:

В этом случае поверхности уровня имеют структуру, сильно отличающуюся от сферической.

Такие функции называются овражными.

Определение 6.4

Степень овражности характеризуется числом:

Обычно при k>10 функция приобретает овражную структуру.

Определение 6.5

Если собственные значения матрицы Гессе удовлетворяют неравенствам:

а отношение:

невелико ,то число называется размерностью оврага.

Решение:

Составим матрицу Гессе:

Найдем собственные значения матрицы Гессе:

Степень и размерность овражности , следовательно, функция имеет овражную структуру.

График функции и линии уровней построим в средеMathCAD 14

Линии уровней:

Как видно из рисунка, лини уровней сильно вытянуты, что указывает на овражность данной функции.

7. Безусловная оптимизация неквадратичной функции овражной структуры. Метод Дэвидона-Флетчера-Пауэлла

Постановка задачи

В курсовой работы предложено написать реализацию метода Дэвидона-Флетчера-Пауэлла на любом алгоритмическом языке. Произвести минимизацию неквадратичной функции двух переменных

, а так же отладить функцию на квадратичной овражной функции, взятой из пункта 6.

В курсовой работы предложено написать реализацию метода Дэвидона-Флетчера-Пауэлла на любом алгоритмическом языке.

Метод Давидона – Флетчера – Пауэла.

Первоначально метод был предложен Дэвидоном (Davidon [1959] ), а затем развит Флетчером и Пауэллом (Fletcher, Powell [1963] ). Метод Дэвидона-Флетчера-Пауэлла называют также и методом переменной метрики. Он попадает в общий класс квазиньютоновских процедур, в которых направления поиска задаются в виде -Dj f(y). Направление градиента является, таким образом, отклоненным в результате умножения на -Dj , где Dj - положительно определенная симметрическая матрица порядка n х n, аппроксимирующая обратную матрицу Гессе. На следующем шаге матрица Dj+1 представляется в виде суммы Dj и двух симметрических матриц ранга один каждая. В связи с этим схема иногда называется схемой коррекции ранга два.

Среди алгоритмов многомерной минимизации следует выделить группу алгоритмов, которые объединяют достоинства метода наискорейшего спуска и метода Ньютона. Такие алгоритмы принято относить к так называемым квазиньютоновским методам. Особенность этих алгоритмов состоит в том, что при их применении нет необходимости вычислять и обращать матрицу Гессе целевой функции f(x) и в то же время удается сохранить высокую скорость сходимости алгоритмов, присущую методу Ньютона и его модификациям.

Алгоритм метода

1. Ввод начальных данных с клавиатуры:

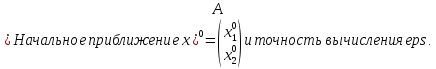
2) Проверка условия:

А) Если утверждение верно, то 5);

Б) Если утверждение ложно, то 3).

3) Нахождение значения :

Где

4) Переопределение значений:

Увеличиваем счетчик итераций и переходим к Шаг2);

5) Минимум найден:

Решение задачи

График и линии уровня заданной функции представлены на рисунках:

Рис.7.1

Функция определена при:

, если условия не выполняются, то программа прекращает свою работу. Данной условие осуществлено за счет проверки знака определителя матрицы Гессе.

При нахождении минимума целесообразно брать точки недалекие от значения минимума функции. Как видно из рисунка 7.1 ,резко возрастает точки должны быть близкими к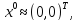иначе функция резко увеличивает количество итераций для, требуемых для нахождения минимума, из-за непрерывного увеличения степени овражности, при отклонении от точки(рис 7.2).

Результат работы программы:

Рис. 4.3

- начальная точка

Программа нашла минимум исходной функции за 2 итерации.

Значение функции 1.902631.903.

Выполним проверку при помощи пакета Mathcad 14: