4.Исследование множества на выпуклость

Постановка задачи:

Доказать, что множество Х решений произвольной системы линейных уравнений и неравенств выпукло.

Теоретические сведения:

Определение 4.1.

Множество называется выпуклым, если любые две точки можно соединить прямой, принадлежащей этому множеству.

Графически это выглядит так:

Математически данное свойство выражается, как:

Данных сведений достаточно, что бы решить поставленную задачу.

Решение:

Пусть произвольная системы линейных уравнений и неравенств имеет вид:

Это ее матричная запись., которая является более удобной.

Так же пусть существуют решения данной системы, т.е. и число.

Тогда два решения этой системы можно записать так:

В силу линейности каждого уравнения произвольная системы линейных уравнений и неравенств имеем:

Объединяя две системы, получим:

В силу дистрибутивности свойств умножения матриц уравнение переписывается в виде:

Т.е. при заданных решениях произвольной системы линейных уравнений и неравенств и числевектор- тоже решение.

Отсюда следует выпуклость множества Х - решений произвольной системы линейных уравнений и неравенств.

5.Исследование функции на выпуклость

Постановка задачи:

Показать, что произведение выпуклых функций необязательно выпукло. Существуют ли подклассы выпуклых функций, замкнутые по отношению к умножению?

Теоретические сведения:

Определение 5.1

Функция где- выпуклое множество, называется выпуклой функцией на этом множестве, если

Теорема 5.1

Пусть функция определена на интервалеи-некоторая точка этого

интервала. При всех определено разностное отношение – функция :

Тогда функция выпукла на интервалев том и только том случае, когда функция

не убывает на множестве .

Теорема 5.2

Пусть функция дифференцируема на интервале и, при всех.

Тогда возрастает на. Если жепри всех, то

не убывает на .

Аналогично, если , при всех , тоубывает на, а если

, при всех , тоне возрастает на.

Теорема 5.3

Пусть функция имеет напроизводную. Функциявыпукла на

тогда и только тогда, когда производная не убывает на.

Замечание 5.1

Дифференцируемая функция вогнута на интервале тогда и только тогда, когда её

производная не возрастает.     

Если функция имеет во всех точках интервала вторую производную , то для

исследования выпуклости можно воспользоваться следующим утверждением.

Теорема 5.4

Пусть на интервале функцияимеет вторую производную. Функция

выпукла на тогда и только тогда, когда, при всех, и вогнута

тогда и только тогда, когда при всех.

Решение:

 Согласно теореме 5.4, если функция выпуклая и имеет вторую производную,то:

при всех .

Например возьмем выпуклые функции , а их

произведение уже не будет выпуклой функцией: так как

Это наглядно представлено на рисунке:

Y

X

Чтобы произведение функций было выпукло, требуется что функции принадлежали к

подклассу выпуклые неотрицательные неубывающие функции.

Тогда их произведение будет положительно :

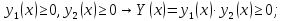
Производная произведения не убывает :