Государственное образовательное учреждение высшего профессионального образования

«Московский государственный технический университет имени Н.Э. Баумана»

(МГТУ им. Н.Э. Баумана)

Аэрокосмический факультет

Кафедра: Вычислительной математики

и математической физики.

Курсовая работа

по предмету:

«Методы конечномерной оптимизации»

Выполнил:

Студент группы АК3-51

Прошин В.В.

Руководитель:

к.т.н.,доц.

Бушуев Александр Юрьевич

Москва 2012 год

СОДЕРЖАНИЕ:

1. Одномерная оптимизация..................................................................................................................3

Метод «золотого сечения».................................................................................................................5

2. Условная нелинейная оптимизация

Применение теоремы Джона-Куна-Таккера..................................................................................6

3. Линейное программирование. Симплекс-метод…………………………………………………17

4. Исследование множества на выпуклость…………………………………………………...…….24

5. Исследование функции на выпуклость…………………………………………………………...25

6. Исследование функции на овражность…………………………………………………………...27

7. Безусловная оптимизация неквадратичной функции овражной структуры.

Метод Дэвидона-Флетчера-Пауэлла………………………………………………………………30

8. Сведение задачи условной оптимизации к безусловной задаче оптимизации…………………35

8.1.Метод внешних штрафных функций….………………………………………………………35

8.2.Метод возможных направлений Зойтендейка……….……………………………………….39

9. Вывод………………………………………………………………………………………………..49

10. Список литературы…………………………………………………………………………………50

11. Приложения

11.1. Одномерный поиск. Метод «золотого сечения»……………………...................................51

11.2. Многомерный поиск минимума функций и добавленный метод внешних штрафных функций. Метод Дэвидона-Флетчера-Пауэлла……………………………………………………………...55

1.Одномерная оптимизация. Метод «золотого сечения»

Постановка задачи:

Изготавливается закрытый цилиндрический бак объема V. Требуется определить такие размеры, для которых затраты на количество материала будут минимальны.

Теоретические сведения:

Определение 1.1

Точка называется точкой глобального (абсолютного) минимума (максимума) функциина множестве, если функция достигает в этой точке своего наименьшего (наибольшего) значения, т.е.

Определение 1.2

Точка называется точкой локального (относительного) минимума (максимума) функциина множестве, если существует, такое, что, если, то.

Здесь - норма вектора в конечномn-мерном евклидовом пространстве.

Теорема 1.1 (необходимые условия экстремума первого порядка)

Пусть есть точка локального минимума (максимума) функциина множествеидифференцируема в точке. Тогда аргумент функциив точкеравен нулю, т.е.

или

Теорема 1.2 (достаточные условия экстремума первого порядка)

Пусть функция в точкедважды дифференцируема, ее градиент равен нулю, а матрица вторых производных является положительно определенной (отрицательно определенной), т.е.

и

, тогда точка есть точка локального минимума (максимума) функциина множестве.

Решение:

На основе геометрических формул записываем целевую функцию задачи. Она имеет вид:

(1)

, что соответствует формуле площади поверхности закрытого цилиндра с параметрами радиуса r и высоты h.

Т.к. в задаче указано, что у бака фиксированный объем, то можно записать уравнение связи между параметрами бака, т.е.:

(2)

Уравнение (2) дает возможность свести задачу минимизации целевой функции от двух параметров к одномерной минимизации целевой функции одного параметра, например:

(3)

Используя необходимые и достаточные условия экстремума функции:

(4)

, заключаем, что точка экстремума целевой функции существует, единственна и она является точкой глобального минимума.

С учетом уравнения связи (2) получаем решение:

(5)

Множество оптимальных параметров, в условиях нашей задачи, может быть описано системой:

(6)

Программная реализация данной задачи методом «золотого сечения» находится в приложении 11.1.

Метод «золотого сечения»:

«Золотым сечением» отрезка называется такое разбиение отрезка на две неравные части, что отношение длины всего отрезка к длине большей части равно отношению длины большей части к длине меньшей части отрезка.

«Золотое сечение» отрезка осуществляется каждой из двух симметрично расположенных относительно центра отрезка точек:

Алгоритм:

(шаг 1)Находим точки, осуществляющие «золотое сечение» отрезка из системы:

, где

(шаг 2) Сравниваем значения функций в точках «золотого сечения»

-Если

-Если

(шаг 3) Проверяем условие остановки алгоритма

, если не выполняется, переходим на (шаг 1),

иначе вычисляем точку минимума

2. Условная нелинейная оптимизация. Применение теоремы Джона-Куна-Таккера

Постановка задачи:

Требуется решить задачу вида:

Теоретические сведения:

Определение 2.1

Обобщенной функцией Лагранжа называется функция вида:

, где - множители Лагранжа

Определение 2.2

Градиентом обобщенной функции Лагранжа по х называется вектор-столбец, составленный из ее частных производных первого порядка ():

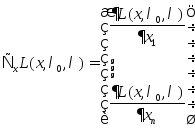
Определение 2.3

Вторым дифференциалом обобщенной функции Лагранжа называется функция:

Определение 2.4

Первым дифференциалом ограничений называется функция:

Определение 2.5

Ограничение называется активным в точке, если. Если, то ограничение называется пассивным.

Определение 2.6

Градиенты ограничений являются линейно независимыми в точке, если равенство

выполняется только при , иначе градиенты ограниченийлинейно зависимы.

Определение 2.7

Точка называется регулярной точкой минимума (максимума), если градиенты ограничений являются линейно независимыми (), иначе точканазывается нерегулярной точкой минимума (максимума).

Теорема 2.1 (Джона-Куна-Таккера) (необходимые условия минимума (максимума) первого порядка)

Пусть - точка локального минимума (максимума) в данной задаче, тогда найдется такое числои вектор, не равные одновременно нулю, что выполняются условия:

а) Условие нетривиальности:

б) Условие стационарности обобщенной функции Лагранжа:

в) Условие допустимости решения:

г) Условие согласования знаков:

д) Условие дополняющей нежесткости:

Теорема 2.2(достаточные условия минимума (максимума) первого порядка)

Пусть имеется точка , удовлетворяющая системе уравненийтеоремы 2.1 при , число активных ограничений в точкесовпадает с числомпеременных (при этом условие регулярности выполняется, т.е. градиенты активных ограничений в точкелинейно независимы). Еслидля всех, то точка- точка условного локального минимума. Еслидля всех, то- точка условного локального максимума.

Теорема 2.3(достаточное условие экстремума второго порядка)

Пусть имеется точка , удовлетворяющая системе уравненийтеоремы 2.1 при .

Если в этой точке для всех ненулевыхтаких, что

То точка является точкой локального минимума (максимума) в данной задаче.

Замечание 2.1

Если функции выпуклые, то условиятеоремы 2.1 являются одновременно и достаточными условиями глобального минимума

Определение 2.8

Функция называется выпуклой вниз (или просто выпуклой) на множестве , если график функции идёт не выше хорды, соединяющей любые две точки графикаи, при

Решение:

Перепишем условие

(ШАГ 1)

Составим обобщенную функцию Лагранжа:

(ШАГ 2)

Запишем необходимые условия экстремума первого порядка:

а) Условие нетривиальности:

б) Условие стационарности обобщенной функции Лагранжа:

или

в) Условие допустимости решения:

г) Условие согласования знаков:

д) Условие дополняющей нежесткости:

(ШАГ 3)

Решаем систему

для двух случаев:

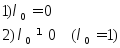
Тогда получаем две системы для рассмотрения:

1. Рассмотрим случай и соответствующие емувариантов (различных комбинаций), удовлетворяющих условию дополняющей нежесткости:

Такие множители Лагранжа приводят к тривиальному решения данной задачи.

Из второго уравнения получаем, что , что не удовлетворяет условию нетривиальности решения.

Система перепишется как:

Видно, что в данном случае решение существует только при , что не удовлетворяет условию нетривиальности решения.

Видно, что решение можно найти из последних двух уравнений системы, т.е.:

Решение данного уравнения находится в множестве комплексных чисел . Такие корни не удовлетворяют условию задачи, что, следовательно, существует только тривиальное решение.

2. Рассмотрим случай и соответствующие емувариантов (различных комбинаций), удовлетворяющих условию дополняющей нежесткости:

Из первых двух уравнений получаем:

Полученную точку следует проверить на выполнение условий, записанных на (шаге 2).

Условия выполняются. Активное ограничение: . Пассивное ограничение:.

Из системы получаем:

Полученные точки проверяем на выполнение условий, записанных на (шаге 2).

Все три точки не лежат в допустимом множестве решений.

Из системы получаем:

Для полученного множителя Лагранжа находим точку:

Проверяем необходимые условия минимума на (шаге 2).

Условия не выполняются, т.к. , что удовлетворяет точке условного максимума. Активное ограничение:. Пассивное ограничение:.

Корни находятся так же как при случае в пункте 4, где нет действительных корней.

Таким образом, имеем одну точку условного экстремума , прис одним активным ограничением.

(ШАГ 4)

Для получено на (шаге 3) точки проверяем достаточные условия минимума первого порядка теорема 2.2.

Т.к. число активных ограничений меньше числа переменных и множители Лагранжа не удовлетворяют достаточным условиям минимума первого порядка, то проверяем условия минимума второго порядка

теорема 2.3.

Запишем второй дифференциал обобщенной функции Лагранжа с учетом :

или

Видно, что второй дифференциал функции Лагранжа положителен, т.е.:

По теореме 2.4 заключаем, что точка есть точка условного локального минимума.

Докажем выпуклость функции :

Построим график целевой функции с помощью средыMathCAD 14.

И его линии уровня:

Т.к. допустимое множество выпукло, ввиду факта односвязности множества и функция является непрерывной (смещенный относительно центра параболоид), то из определения 2.8 заключаем, что функция выпукла. Так что, используя замечание 2.1, получаем, что точка

есть точка глобального минимума.

(ШАГ 5)

Перепишем целевую функцию:

Ее значение в точке - глобального минимума есть