2.3. Опис роботи ідеального приймача

Нехай протягом часу (0, τ_i) тривалості одного елемента сигналу аналізується прийняте коливання:

де A_i(t) – переданий i-й корисний сигнал; B(t) – флуктуаційна завада у вигляді білого гауссівського шуму.

Апріорні ймовірності P(A_i) появи i-го елемента сигналу A_i(t) є відомими. Приймач повинен вирішити статистичну задачу про те, який елемент сигналу йому був переданий (A₁, A₂,…, A_m,). Коротко це правило будемо називати правилом вирішення, а схему, що працює по алгоритму цього правила – вирішальною схемою.

Оскільки у викладках, що наводяться нижче, завадостійкість оцінюється відносно флуктуаційної завади, то оптимальне правило вирішення буде визначатися для нормального розподілу миттєвих значень завади з густиною ймовірності:

.

Нехай приймач виносить рішення по результату обчислення сумісної апостеріорної ймовірності n відліків коливання, що приймається. Тоді, апостеріорні ймовірності будуть мати вигляд:

Де - умовна густина ймовірності, що обчислена для сукупності прийнятих значеньприйнятої реалізації.

Якщо відліки є статистично незалежними, то:

де 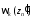- умовна густина ймовірності, що обрахована для одиночного відліку.

Для нормального закону розподілу:

де - значення сигналуА_k(t) в l-й момент відліку.

Відповідно, отримаємо:

.

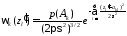Нехай коливання Z(t), сигнал А_k та завада у точках відліку визначаються середніми значеннями:

, ,.

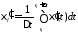де ,n – кількість відліків.

Тоді:

,

де .

У відповідності до загального принципу реєстрації сигналів по критерію максимуму апостеріорної ймовірності, правило вирішення можна сформулювати наступним чином:

1. Реєструється сигнал A_i(t), якщо виконується нерівність:

2. Сигнал A_j(t) у протилежному випадку.

Отже, правило вирішення у аналітичному вигляді можна записати як:

.

При необмеженому зменшенні інтервалу Δt шляхом граничного переходу та логарифмування, отримаємо:

.

де – питома інтенсивність (середня потужність у полосі 1 Гц) флуктуаційної завади,- прийнята реалізація коливанняZ(t),

A_i(t) і A_j(t) – сигнали, апостеріорні ймовірності яких порівнюються між собою.

Далі піднесемо до квадрату попередню формулу. Можна показати, що в цьому випадку:

,

де 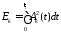- енергія переданого елемента сигналу.

Отримана формула, в загальному випадку, є формулою, що визначає алгоритм роботи ідеального приймача. Функціональна схема приймача, що реалізує даний алгоритм, зображена на рис.2.3.

Схема має m гілок обробки сигналу, що передається. Кожна з цих гілок узгоджена з одним із m сигналів. Процедура обробки включає в себе множення прийнятого коливання з даним сигналом, їх інтегрування та віднімання з отриманого результату рівня .

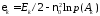Кожен i-й відлік Z_i є результатом обробки коливання Z(t) в інтервалі (0,τ_i) у припущенні, що був переданий i-й елемент сигналу. Величина Z_i пропорційна апостеріорній ймовірності.

Рис.2.3. Структурна схема ідеального приймача

З алгоритму роботи ідеального приймача випливає, що для його реалізації необхідно на приймальному боці каналу зв’язку точно знати такі дані:

1. копії переданих елементів сигналу A₁(t), A₂(t),….A_m(t);

2. енергії переданих елементів E₁, E₂,…,E_m;

3. апріорні ймовірності появи кожного з елементів сигналу;

4. спектральну щільність потужності шуму G₀;

5. часові межі елементів сигналу (0,τ_i).

У системах зв’язку в основному використовується двійкові сигнали. При цьому апріорні ймовірності для обох символів однакові, і рівні 0,5. У цьому випадку загальний алгоритм роботи ідеального приймача спрощується:

,

(2.1)

де Е₁ та Е₂ - енергії відповідно елементів A₁(t) та A₂(t).

Зауважимо, що послідовно з’єднана схема множення та інтегрування називається корелятором, оскільки вона визначає функцію взаємної кореляції між двома коливаннями Z(t) A_i(t) де i=1,2.