3.3 Проверка качества зубьев

Проверка на незаострение.

Полагая, что рабочие поверхности зубьев проэктируемых колес подвергнуты термообработке, предъявляем следующие требования к их толщине по окружности вершин:

Зубья не заострены.

Проверка на отсутствие подрезания.

Зуб считается подрезаным, если в процессе нарезания срезается часть эвольвенты у ножки зуба.

0,5 · 13 · 1 – 0,543

0,5 · 24 · 1 – 0,457

Подрезание зубьев отсутствует.

Коэффициент перекрытия обеспечивает плавность зацепления, так как

3.4 Построение эвольвентного зацепления

Принимаем масштаб для вычерчивания картины зацепления 5:1.

Отложив в выбранном масштабе межосевое расстояние проводим начальные окружности, основные окружности и линию зацепления, которая должна пройти через полюс зацепления и быть общей касательной к основным окружностям, опускаем перпендикулярыииз центровина линию зацепления.

Строим эвольвенты, которые описывает точка прямой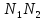при перекатывании ее по основным окружностям без скольжения. Для построения эвольвенты шестерни делим отрезокна 8 равныx части – получаем точки 1…8 . Далее от точкиоткладываем по основной окружности вправо столько же отрезков.

Проводя в этих точках касательные к основным окружностям и откладывая на них отрезки длиной: на первой касательной – 1 отрезок от точки касания, на второй касательной – 2 отрезка от точки касания и т.д., получим точки зуба шестерни.

Аналогично строятся точки зуба колеса, при этом делится отрезок.

Проводим окружности впадин. Проводим делительные окружности. От каждой эвольвенты откладываем по делительной окружности отрезок равный , получим точку, через которую пройдет ось симметрии зуба. Затем строим профиль каждого зуба.

Для построения соседнего зуба, от оси симметрии построенного зуба откладываем по делительной окружности расстояние равное ,получим точку лежащую на оси симметрии следующего зуба.

3.5 Синтез планетарного редуктора и определение угловых скоростей звеньев редуктора аналитическим методом

Подбор чисел зубьев колесипланетарного механизма производится на ПК.

Определим исходные данные, необходимые для подбора чисел зубьев.

Зубчатый механизм состоит из последовательно соединенной планетарной передачи (колеса 1, 2, 3, 4 и водило Н) и простой передачи 5-6. Найдем передаточное отношение редуктора в соответсвии с теоремой об общем передаточном отношении.

Передаточное отношениепредставим в виде:

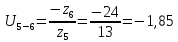
Тогда для планетарной ступени:

Угловая скорость первого колеса редуктора:

Допустимое отклонение передаточного числа .

Используя программу подбора чисел зубьев по заданному и с учетом условий: соосности, соседства и сборки (т.к. устанавливаются 3 блока сателлитов), получаем таблицу, из которой выбираем вариант №2

126

Определим фактическое передаточное отношение. Для этого применим метод обращения движения механизма: для этого водило Н сделаем неподвижным, а остальным звеньям планетарной передачи добавим угловую скорость ( - ). При этом водило остановиться и планетарный механизм превращается в простой. Получаем обращенный механизм.

Откуда получим:

Относительная погрешность будет равна:

∆

Определяем угловые скорости звеньев:

Из следует

Из следует

Из ;

=25.82 рад/с

Условие соседства имеет вид

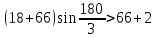
72.7568

Условие соседства выполняется

Условие соосности имеет вид:

18+66=126-42

84=84

Условие соосности выполняется

Условие сборки имеет вид:

Целое число, следовательно, условие сборки выполняется.