Державний вищий навчальний заклад «Донецький національний технічний університет» Кафедра «Основи проектування машин» курсова робота

з теорії механізмів і машин

на тему: «Спроектувати та дослідити важільний та зубчастий механізми»

Студента III курсу групи КПМО-10

напряму підготовки інженерна механіка

спеціальності КПМО

Бояринов С.В.

Керівник старший викладач

Пархоменко В.Г.

Національна шкала _____________

Кількість балів:__________ Оцінка ECTS____

м. Донецьк – 2012 рік

Реферат

Курсовий проект: 27 сторінок, 8таблиць, 2додатки на листах формату А1.

Об'єкт проектування та дослідження –важільний та зубчастий механізми.

Мета роботи – синтез і аналіз цих механізмів.

При проектуванні і дослідженні механізмів використані графічні і аналітичні методи з використанням ЄОМ.

ВАЖІЛЬНИЙ МЕХАНІЗМ, ШВИДКОСТІ, ПРИСКОРЕННЯ, МОМЕНТ, МЕТОД БРУЄВИЧА, СПОСІБ ЖУКОВСЬКОГО, ПЛАНЕТАРНИЙ МЕХАНІЗМ, ЗУБЧАСТА ПЕРЕДАЧА, ЕВОЛЬВЕНТА, ПЛАНЕТАРНИЙ МЕХАНІЗМ, МЕТОД ВІЛЛІСА, САТЕЛІТ.

Содержание

Введение 4

1. КИНЕМАТИЧЕСКОЕ ИССЛЕДОВАНИЕ СТЕРЖНЕВОГО МЕХАНИЗМА

1. Структурный анализ механизма 5

2. Построение плана механизма 5

3. Построение плана скоростей для нулевого положения 6

4. Построение плана ускорений для нулевого положения 7

5. Построение плана скоростей для заданного положения 9

6. Построение плана ускорений для заданного положения 10

1. СИЛОВОЙ АНАЛИЗ СТЕРЖНЕВОГО МЕХАНИЗМА ДЛЯ ЗАДАННОГО ПОЛОЖЕНИЯ 12

   1. Определение уравновешивающего момента по методу Бруевича 13

   2. Определение уравновешивающего момента по правилу Жуковского 14

2. СИНТЕЗ ЗУБЧАТОГО ЗАЦЕПЛЕНИЯ И РЕДУКТОРА 15

   1. Расчет геометрических параметров эвольвентного зацепления 15

   2. Вычисление контрольных размеров, которые проставляются на чертеже 17

3.3 Проверка качества зубьев 19

3.4 Построение эвольвентного зацепления 20

3.5 Синтез планетарного редуктора и определение угловых скоростей звеньев

редуктора аналитическим методом 21

3.6 Кинематическое исследование редуктора 23

ВЫВОД 26

СПИСОК ЛИТЕРАТУРЫ 27

Введение

1. Кинематическое исследование стержневого механизма

1. Структурный анализ механизма

Механизм состоит из четырех звеньев и четырех кинематических пар.

1—кривошип (вращательное);

2—шатун (плоскопараллельное);

3—коромысло (возвратно вращательное);

4—стойка (неподвижная);

Классификация кинематических пар:

1-4: плоская, относительное движение—вращательное, геометрически замкнутая, низшая, одноподвижная пара;

1-2:плоская, относительное движение—вращательное, геометрически замкнутая, низшая, одноподвижная пара;

2-3:плоская, относительное движение—вращательное, геометрически замкнутая, низшая, одноподвижная пара;

3-4:плоская, относительное движение—вращательное, геометрически замкнутая, низшая, одноподвижная пара;

Определим степень подвижности звеньев:

Степенью подвижности механизма называется число независимых координат, однозначно определяющих положение всех звеньев механизма в системе координат, жёстко связанных с неподвижной точкой (стойкой).

Так как механизм плоский, т.е. все его звенья расположены в одной плоскости, то степень подвижности механизма будем определять по формуле Чебышёва П.Л.:

где – количество подвижных звеньев механизма;

–количество одноподвижных пар;

–количество двуподвижных пар;

То есть данному механизму достаточно задать одну обобщённую координату, для того чтобы определить положения всех звеньев в заданный момент времени относительно выбранной неподвижной системы координат (её обычно связывают со стойкой).

Структурный анализ механизма проводят путём разделения его на структурные группы и начальные механизмы в порядке, обратному его созданию, то есть начиная с последней присоединительной группы Ассура.

Структурная группа (группа Ассура) – это кинематическая цепь, присоединение которой к механизму не изменяет количество его степени свободы.

В целом, механизм второго класса, образован путем последовательного присоединения к механизму первого класса (1,4), механизма II-го класса (2,3).

Формула строения механизма:

.

2. Построение плана механизма

Для построения плана механизма принимаем масштабный коэффициент .

Масштабный коэффициент представляет собой отношение действительной величины некоторого физического параметра, размерность которого берётся в системе СИ, к изображению этой величины на плане, взятому в миллиметрах.

Зададим, на чертеже, начальное положение точки О₁. Строим окружность, радиусом О₁А, и разбиваем ее на 12 равных частей. Отложив от точки О₁ по горизонтали значение a=0.11 м, а по вертикали значение b=0,28м, находим местоположение точки О₂. Проведем окружность, с центром в точке О₂ и радиусом О₂В.

Из точки О₁ проводим окружность радиусом О₁В=О₁А+АВ. Точкой пересечения окружности О₁В и О₂В будет точка . Из точки В, через точку А, проводим отрезок ВС=0,48м, таким образом получаем точку С. Данную процедуру повторяем для всех остальных 11 точек. Получим 12 положений механизма.

За начальное положение механизма, принимаем крайнее правое положение звена О₂В. Нумерацию положений производим по направлению вращения кривошипа. За заданное положение механизма, принимаем положение звена О₁А, повёрнутое относительно начального положения на угол . Это десятое положение механизма.

3. Построение плана скоростей для нулевого положения

Построение плана скоростей начинается с определения вектора скорости точки А, которая принадлежит кривошипу 1 (Рис.1). Кривошип вращается вокруг оси, которая проходит через точку О1, линейная скорость которой.

Скорости точек О₁ и О₂ равняются нулю, потому их изображения о₁ и о₂ находятся в полюсе плана.

, м/с

м/с

Направляем вектор по направлению вращения кривошипа.

На плане скоростей обозначаем его отрезком. Масштабный коэффициент принимаем равным

,

;

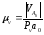Точка А₀ одновременно принадлежит двум звеньям – кривошипу 1 и шатуну 2, а точка В₀ шатуну 2 и коромыслу 3.

Шатун 2 двигается плоско-параллельно, следовательно розложив плоское движение на переносное – поступательное движение вместе с точкой А₀ и относительное – вращательное движение звена вокруг оси ,которая проходит через точку А₀, получаем:

,

Уравнение для определения скорости точки В будет иметь вид:

,

Вектор относительной скорости направлен по касательной в сторону вращения точки В₀ вокруг точки А₀ ().

Вектор абсолютной скорости точки В₀, направленный по касательной к траектории абсолютного движения точки В₀звена 3 – вращение вокруг оси, которая проходит через точку 0₂ ().

В векторном выражении две неизвестные величины, его решаем графически: через точку а₀плана скоростей проводим линию, которая перпендикулярна А₀В₀, а через полюс – перпендикуляр к О₂В₀.

Точка пересечения этих векторов будет концом векторови.

Оределим модули этих векторов:

, м/с

, м/с

_{По теореме подобия определим скорость точки С0:}

_{Теорема подобия (свойства) планов скоростей:}

_{Неизменяемой фигуре на плане механизма (звену) на плане скоростей соответствует фигура, подобная и сходственнорасположенная.}

Модуль этого вектора определим как:

Определим значения угловых скоростей звеньев 2,3:

Для определения направления угловой скорости ₂ переносим вектор в точку В₀ плана механизма, тогда видно что ₂ направлена против хода часовой стрелки.

Для определения направления угловой скорости ₃ переносим вектор в точку В₀ плана механизма, тогда видно что ₃ направлена по ходу часовой стрелки.

4. Построение плана ускорений для нулевого положения

Построение плана ускорений начинается с определения ускорения точки А₀, которое раскладывается на нормальное и тангенциальное ускорение точки А₀.

Выбираем масштабный коэффициент

, тогда, на чертеже, длинна вектора ускорения точки А₀будет равна:

мм

Определяем ускорение точки B₀:

Точка В принадлежит звену А₀В₀, которое совершает плоско-параллельное движение. Тогда её ускорение равно:

_{Точка В0принадлежитзвену О2В0. Тогда её ускорение равно:}

_{Решая систему уравнений, определим искомые модули и векторы ускорений.}

Ускорение точки С₀ определяем по теореме подобия

Тога модуль вектора ускорения точки С0:

Определим угловые ускорения звеньев:

ε₂=рад/с;

ε₃=рад/с.

Направление ε₂ получим, если перенесём вектор из плана ускорений в точку В₀ плана механизма и учтём, что центром относительного вращения звена А₀В₀ является точка А₀. Таким образом, ε₂ направлен по ходу часовой стрелки.

Направление ε₃ получим, если перенесём вектор из плана ускорений в точку В₀ плана механизма и учтём, что центром относительного вращения звена В₀О₂ является О₂.Таким образом, ε₃ направлен по ходу часовой стрелки.

5. Построение плана скоростей для заданного положения

,

;

,

,

, м/с;

, м/с;

м/с;

м/с

6. Построение плана ускорений для заданного положения

,

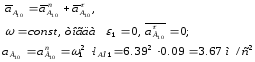
мм

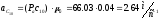
ε₂=рад/с;

ε₃=рад/с.