
- •Курсовая работа (курсовой проект)
- •Задание на курсовую работу
- •Оглавление
- •Введение
- •Финансовые функции
- •Функции анализа кредитов и вкладов
- •Функции, применяемые для вычисления параметров ссуды
- •Функция плт
- •Функция осплт
- •Функция прплт
- •Функция ставка
- •Функция пс
- •Анализ экономической проблемы
- •Терминология
- •Описание функции кпер
- •Аргументы функции кпер
- •Примеры использования функции кпер
- •Пример 1
- •Решение задачи
- •Пример 2
- •Решение задачи
- •Пример 3
- •Решение задачи
- •Список используемой литературы
Примеры использования функции кпер
Пример 1
Дано
В депозитный вклад была внесена сумма размером в 60 000 руб., годовая процентная ставка по вкладу 6% годовых и начисление процентов производится ежемесячно. Необходимо рассчитать, через сколько времени сумма достигнет 120 000 руб.
Решение задачи
При ежемесячном начислении процентов ставка процента за период начисления равна 6%/12. Чтобы определить общее число периодов выплат для единой суммы вклада, воспользуемся функцией КПЕР со следующими аргументами:
ставка = 6%/12;
пс = -60000;
бс = 120000.
Значением функции КПЕР является число периодов, необходимое для проведения операции, в данном случае - число месяцев. В результате мы получим число периодов, равное 138,97. То есть почти 139 месяцев.
Для нахождения числа лет полученный результат разделим на 12. В строке формул запишем =139/12, и получим 11,58. То есть около 11,6 лет.
Иллюстрацию к задаче можно рассмотреть на рисунке 4.
 Рис.
4: иллюстрация к примеру 1
Рис.
4: иллюстрация к примеру 1
Пример 2
Дано
Была взята ссуда на сумму 300 000 руб. под 17% годовых. Объем каждой выплаты равен 7000 руб. Нужно рассчитать количество лет, необходимых для погашения ссуды.
Решение задачи
При ежемесячной плате ставка процента за период равна 17%/12. Чтобы определить общее число периодов выплат по ссуде, воспользуемся функцией КПЕР со следующими аргументами:
ставка = 17%/12;
плт = 7 000;
пс = -300 000.
Значением функции КПЕР является число периодов, необходимое для погашения ссуды, в данном случае - число месяцев. В результате мы получим число периодов, равное 66,42. То есть около 66,4 месяцев.
Для нахождения числа лет полученный результат разделим на 12. В строке формул запишем =66,4/12, и получим 5,53. То есть около 5,5 лет.
Иллюстрацию
к задаче можно рассмотреть на рисунке
5.
Рис. 5: иллюстрация к примеру 2
Пример 3
Дано
Рассмотрим задачу, решенную в пункте 6.2. подробнее, вычислив зависимость числа периодов от изменения процентной ставки, от изменения выплаты, производимой в каждый период и от изменения общей суммы.
Решение задачи
Для этого возьмем имеющиеся данные и составим таблицы зависимости. В таблице зависимости числа периодов от изменения процентной ставки (Рис. 6) мы берем 15 различных значений ставки. Значения платежа и приведенной стоимости остаются неизменными в ячейках A5 иB5 соответственно. Для того, чтобы правильно рассчитать все значения по формуле КПЕР, нужно в строке формул для ячейкиB8 изменить аргументы платежа и приведенной стоимости таким образом, чтобы их значения были закреплены в ячейкахA5 иB5. Для этого рядом с цифрой 5, означающей строку, где находятся значения аргументов, нужно поставить значок доллара ($), нажав при этом необходимое количество раз клавишуF4 или просто приписав значок перед цифрой. После этого достаточно потянуть за правый нижний угол ячейку с формулой, чтобы заполнить все 15 ячеек таблицы.
Аналогично выполним вычисления зависимости числа периодов от изменения выплаты, производимой в каждый период, результаты которых можно увидеть на рисунке 7, вычисления зависимости числа периодов от изменения общей суммы, результаты которых показаны на рисунке 8.
Рис. 6: зависимость числа периодов от
изменения процентной ставки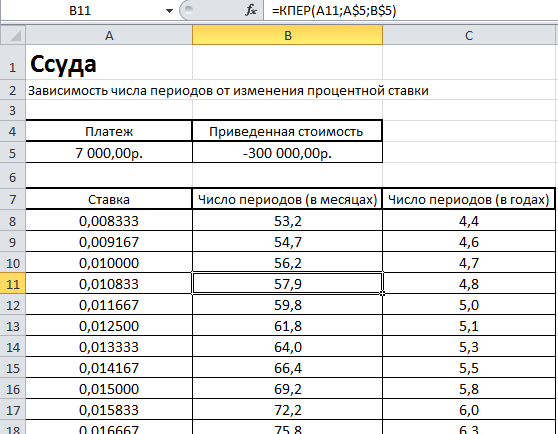

Рис. 7: зависимость числа периодов от изменения выплаты, производимой в каждый период

Рис. 8: зависимость числа периодов от изменения общей суммы
Примеры можно подробно рассмотреть в файле «Примеры применения функции КПЕР.xlsx»
