
- •Тема №1. Тепло земных недр
- •1.1. Термодинамические параметры земной коры
- •1.2. Источники тепла земных недр
- •1.3. Процессы теплопереноса в недрах Земли
- •1.4. Использование тепла земных недр
- •1.5. Приближенные методы расчета температурных режимов при эксплуатации породных теплообменников
- •Тема №2. Промерзание связных пород при открытой разработке месторождений
- •2.1. Разработка связных пород в период с отрицательными температурами
- •2.2. Месячные колебания температуры внешней среды
- •2.3. Расчет глубины промерзания связанных пород
- •2.4. Полное предотвращение промерзания грунта при использовании теплоизоляционных покрытий
- •2.5. Промерзание грунта на допустимую глубину при использовании теплоизоляционного покрытия
- •Тема №3. Намораживание пород при строительстве подземных сооружений и шахт
- •3.1. Сущность способа и область его применения
- •3.2. Тепловой расчет формирования одиночного ледопородного цилиндра
- •3.3. Параметры образования ледопородных ограждений
- •Тема №4. Теплообмен в горных выработках
- •4.1. Требования к тепловому режиму в подземных выработках
- •4.2. Влияние теплового режима на процессы ведения подземных горных работ
- •4.3. Уравнения теплообмена массива с вентиляционной струей в шахтной выработке
- •4.4. Теплообмен при проветривании подземных выработок
- •4.5. Источники тепла в подземных выработках
- •4.6. Методы нормализации температурного режима рудничного воздуха
- •Тема № 5. Термодинамическое разрушение талых и мерзлых пород при их разработке и транспортировании
- •5.1. Проблемы разработки и транспортирования рыхлых и связных пород
- •5.2. Термодинамическое разрушение талых рыхлых и связных пород
- •5.3. Термодинамическое хрупкое разрушение мерзлых рыхлых и связных пород
- •5.4. Термодинамическое разрушение мерзлых рыхлых и связных пород путем оттаивания и абляции
- •5.5. Техника и технология термодинамического разрушения талых и мерзлых пород при их разработке и транспортировании
- •Тема №6 . Газодинамические процессы в горных выработках
- •6.1. Основные понятия и определения. Механизм переноса газообразной субстанции.
- •6.2. Путь перемешивания для содержания газа и газовые потки
- •6.3. Коэффициенты диффузии
- •Тема №7. Интегральные газодинамические эффекты в шахтах
- •7.1. Общие положения
- •7.2. Выработка как объект вентиляции
- •7.3. Ограниченные потоки в системе выработок
2.3. Расчет глубины промерзания связанных пород
Рассмотрим случай промерзания связной породы при открытой разработке месторождений.
Сформулируем задачу: на поверхности полупространства в момент времени t=0 устанавливается отрицательная температура Тв, равная температуре внешней окружающей среды. В процессе промерзания связной породы образуется промерзший слой переменной толщиныh=f(t). Нижняя граница этого слоя всегда имеет температуру замерзания влаги Т.На этой границе происходит фазовый переход «вода-лед», при котором выделяется теплота перехода Lф, Дж/кг. На глубине залегания нейтрального слоя Н0 температура всегда постоянна и равна примерно 277 К (4°С). Обозначим эту температуру через Т0. Кроме этого, условимся обозначать в данной и последующих задачах этой темы параметры теплоизоляционного покрытия индексом 1, промерзшей связной породы — индексом 2 и талой — индексом 3.
Для описания распределения температурного поля в системе «промерзшая связная порода - талая порода» воспользуемся моделью, изображенной на рис. 2.1.
Рис. 2.1. Тепловая модель «промерзший грунт — талый грунт»
Математически задачу можно сформулировать следующим образом: решить дифференциальные уравнения теплопроводности
![]() при 0<х<h
(2.5)
при 0<х<h
(2.5)
![]() при h
<х<∞
(2.6)
при h
<х<∞
(2.6)
при следующем начальном условии
Т2│t=0 = ТВ =соnst (2.71)
Т3│t=0 = Т0 (2.72)
и граничных условиях
Т2│x=0 = ТВ (2.8)
Т2│x=h = Т3│x=h =Т*=соnst (2.9)
![]() (2.10)
(2.10)
где а — температуропроводность грунта, м2/с;
λ — его теплопроводность, Вт/ (м·К);
Lф – теплота фазового перехода «вода-лед», Дж/кг;
W — влажность грунта, кг/кг;
γn — его плотность, кг/м .
Общие решения дифференциальных уравнений (2.5) и (2.6) можно представить в виде:
![]()
![]() (2.11)
(2.11)
![]() (2.12)
(2.12)
где
![]()
Подставляя граничное условие (2.8) в (2.11), получим:
Т2│x=0
= A2+
B2erf![]() =
A2+
B2erf0=
A2=
ТВ
=
A2+
B2erf0=
A2=
ТВ
откуда
A2= ТВ (2.13)
Подставляя начальное условие (2.7) в уравнение (2.12), получим:
Т3│t=0
= A3+
B3erf![]() =
A3+
B3erf∞=
A3+
B3=
Т0
=
A3+
B3erf∞=
A3+
B3=
Т0
откуда
A3= Т0 - B3. (2.14)
С учетом (2.13) и (2.14) общие решения (2.11) и (2.12) примут вид:
Т2=
ТВ
+ B2erf![]() , (2.15)
, (2.15)
Т3=Т0-В2+B3erf![]() =
Т0 -
B3
=
Т0 -
B3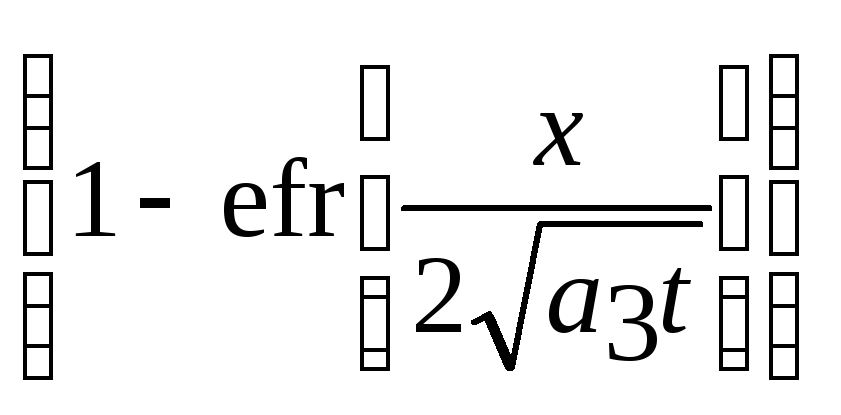 =
Т0-B3erfc
=
Т0-B3erfc![]() ,
(2.16)
,
(2.16)
где
![]()
Согласно (2.9) на глубине промерзания Т2 = Т3 = Т, поэтому уравнения (2.15) и (2.16) при х = h примут вид
Т2=
ТВ
+ B2erf![]() =Т*
= const, (2.17)
=Т*
= const, (2.17)
Т3
= Т0
- B3erfc![]() =Т*=
const (2.18)
=Т*=
const (2.18)
Так как величины Тв, Т0, Т , а1 и а3 есть некоторые постоянные, то уравнения (2.17) и (2.18) будут справедливы в том случае, если будет выполняться условие
![]() (2.19)
(2.19)
или
![]() ,
(2.20)
,
(2.20)
где β
— коэффициент пропорциональности,
характеризующий скорость углубления
зоны промерзания, м/![]() .
.
Подставляя (2.20) в (2.17) и (2.18), получим:
Т2=
ТВ
+ B2erf![]() =
ТВ
+ B2erf
=
ТВ
+ B2erf![]() =
Т* (2.21)
=
Т* (2.21)
Т3
= Т0
+ B3erfc![]() =
Т0
+ B3erfc
=
Т0
+ B3erfc![]() =Т*
(2.22)
=Т*
(2.22)
Из (2.21) и (2.22) соответственно получим
В2=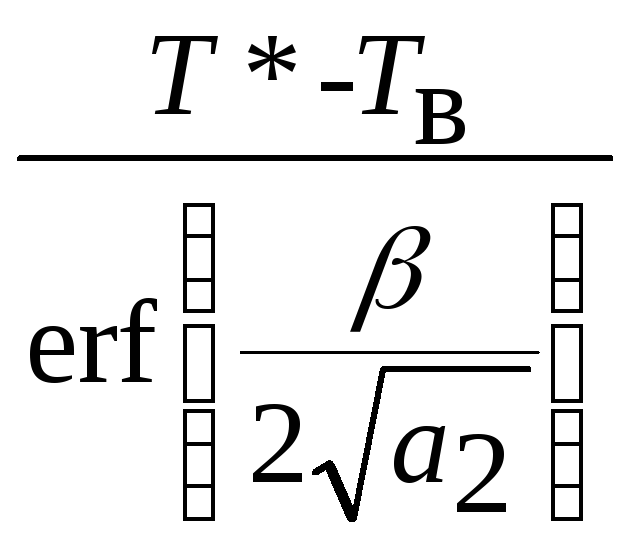 ,
(2.23)
,
(2.23)
В3=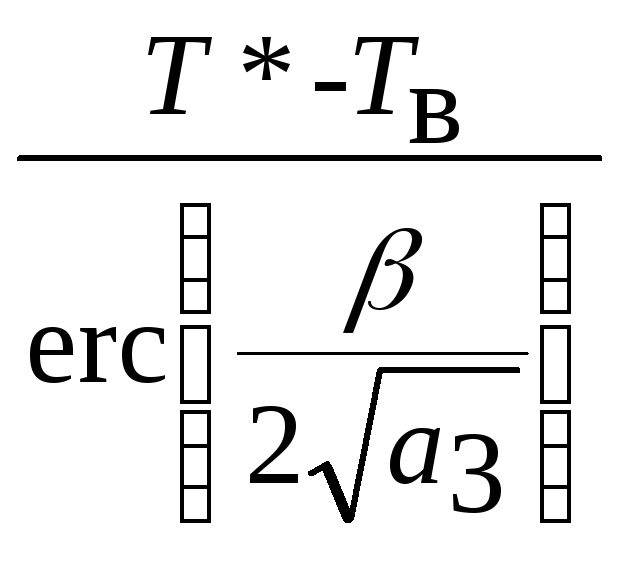 .
(2.24)
.
(2.24)
Подставляя (2.24) в (2.14) получим
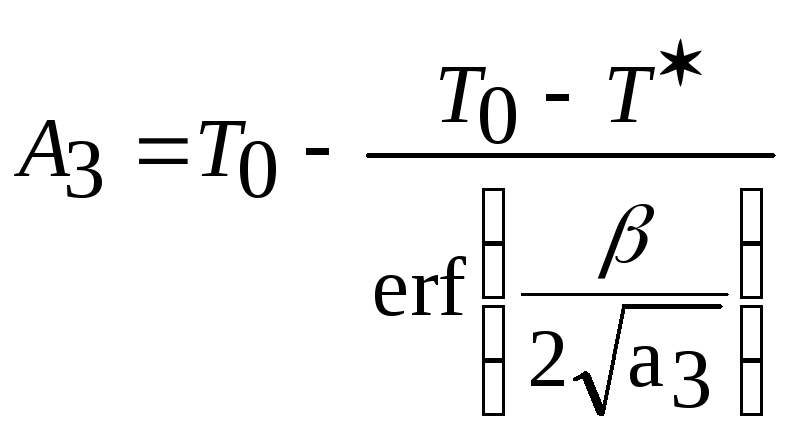
Подставляя (2.23), (2.24) и значение А3 соответственно в (2.15) и (2.16), получим уравнения для оценки поля температур
• в промерзшей зоне
Т2=
ТВ
+(Т*- ТВ)
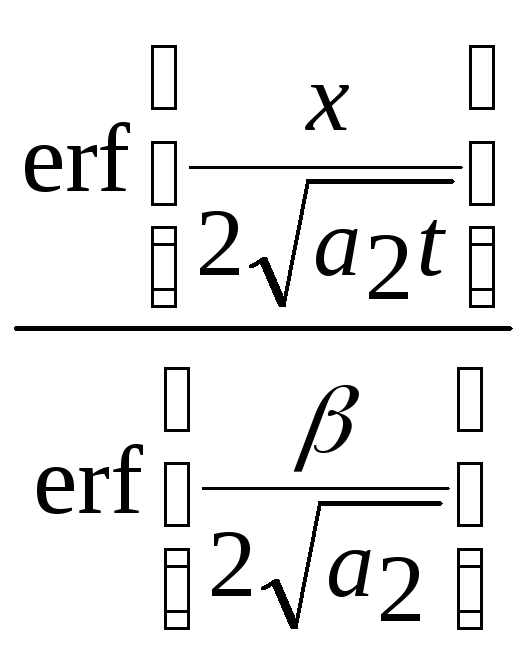 (2.25)
(2.25)
• в талой зоне
Т3=
Т0
-( Т0-Т*)
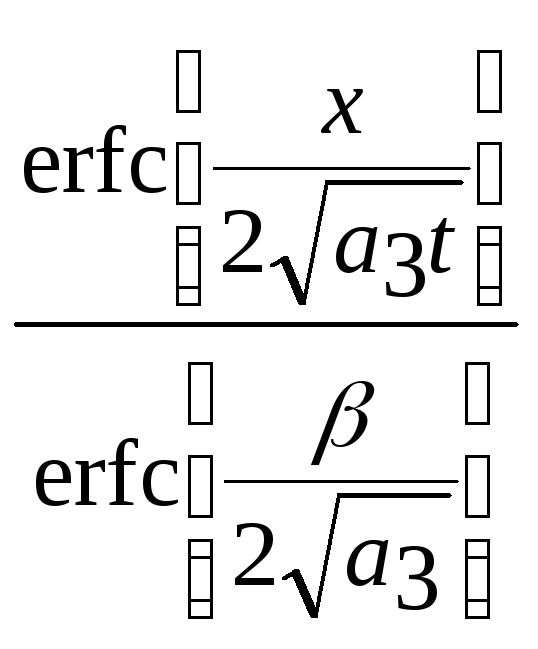 (2.26)
(2.26)
В уравнениях (2.25) и (2.26) неизвестен параметр β. Его определим из условия (2.10). Прежде чем перейти к определению β приведем несколько преобразований, которые понадобятся в дальнейшем:
![]() (2.27)
(2.27)
![]() (2.28)
(2.28)
При x=hграничное условие (2.10) примет вид
![]() (2.29)
(2.29)
Возьмем отдельно производные
![]() и
и![]() ,
входящие в уравнение(2.29),
с учетом значений
,
входящие в уравнение(2.29),
с учетом значений
Т2=
ТВ
+(Т*- ТВ)
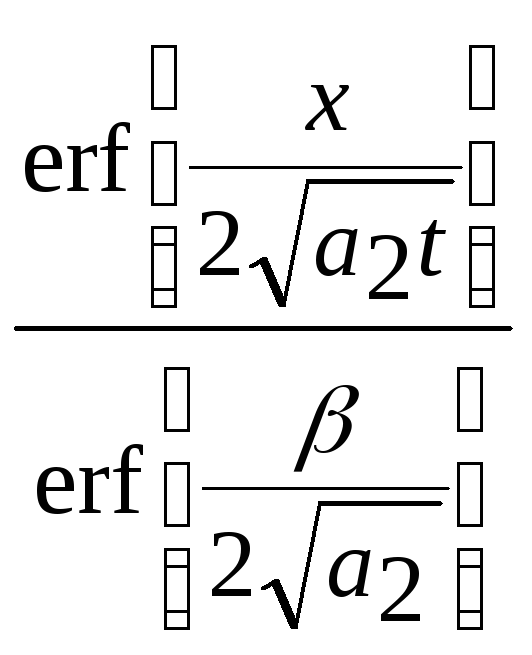 и Т3=
Т0
-( Т0-Т*)
и Т3=
Т0
-( Т0-Т*)
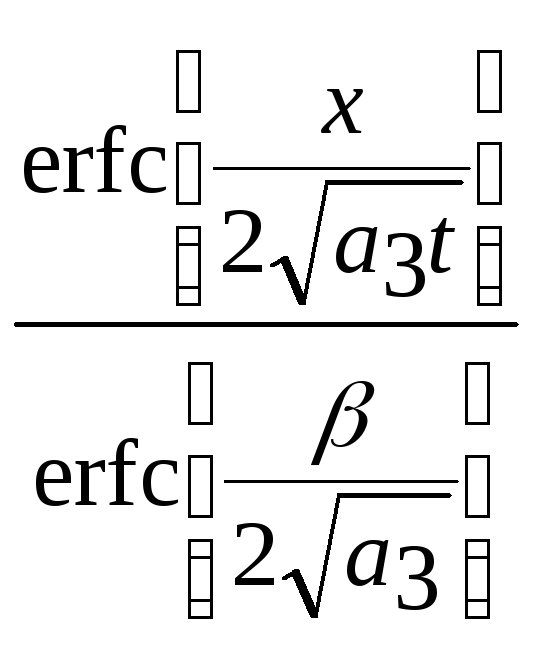
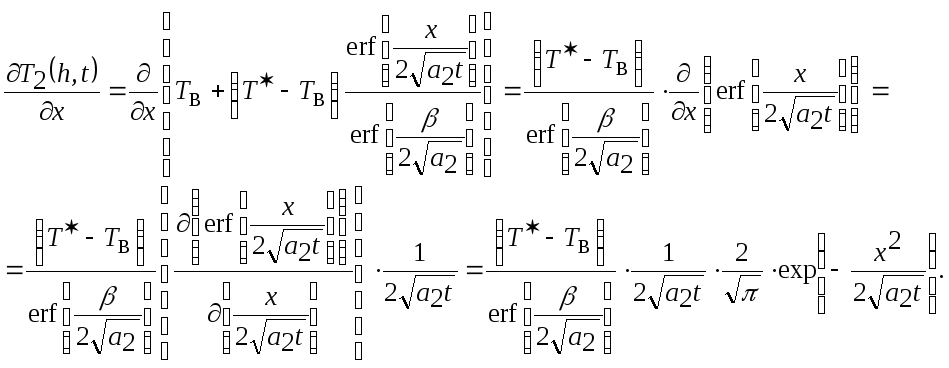 (2.30)
(2.30)
При x=h=![]() выражение
(2.30) примет вид:
выражение
(2.30) примет вид:
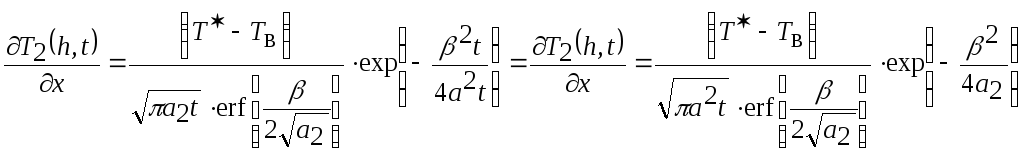 (2.31)
(2.31)
Аналогично
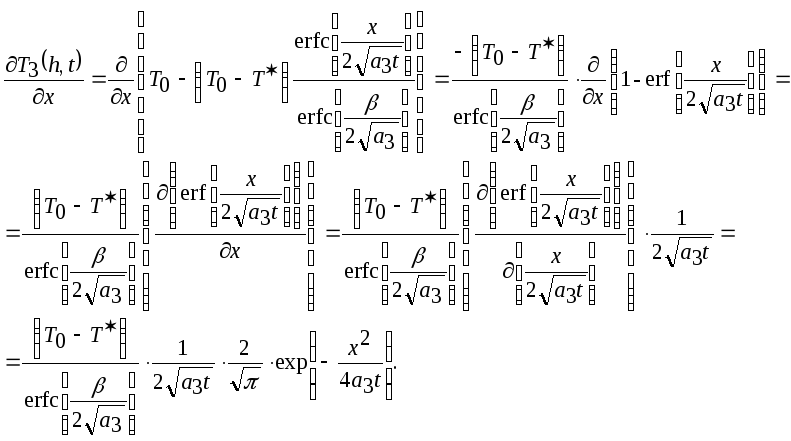 (2.32)
(2.32)
При x=h=![]() выражение
(2.32) примет вид:
выражение
(2.32) примет вид:
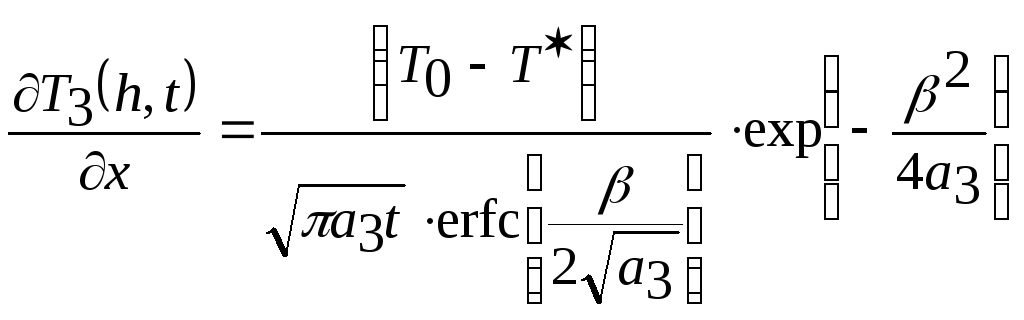 (2.33)
(2.33)
Правая часть уравнения (2.29) при x=h=![]() станет равной
станет равной
![]() (2.34)
(2.34)
Подставляя (2.31), (2.33), (2.34) и (2.29), получим
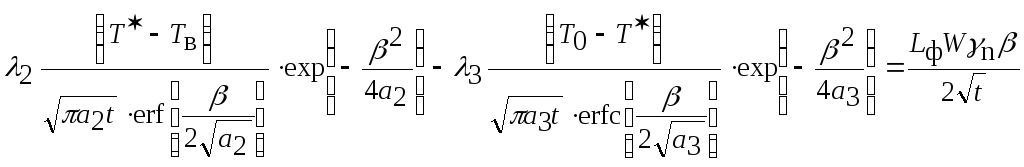 (2.35)
(2.35)
Умножив обе части выражения на
![]() ,
получим конечное трансцендентное
уравнение для определения коэффициентаβ
,
получим конечное трансцендентное
уравнение для определения коэффициентаβ
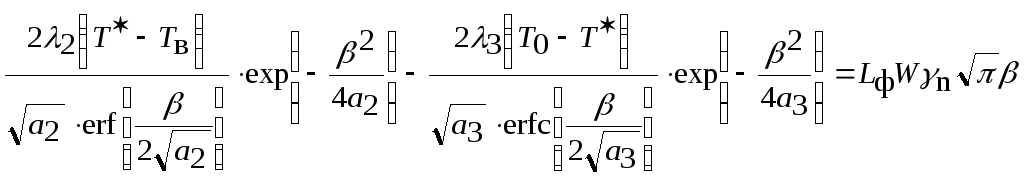 (2.36)
(2.36)
Определив βиз (2.36) как функцию λ2,а2, λ3,а3, Т,
Тв, Т0,Lф,Wиγn,
и принимая во внимание, чтоh=![]() ,
можно определить глубину промерзания
грунта. Кроме этого, знаяβ, согласно
(2.25) и (2.26) можно определить распределение
температурного поля соответственно в
промерзшей и талой зонах грунта.
,
можно определить глубину промерзания
грунта. Кроме этого, знаяβ, согласно
(2.25) и (2.26) можно определить распределение
температурного поля соответственно в
промерзшей и талой зонах грунта.
Если влажность грунта незначительна и ею можно пренебречь, то при граничных условиях первого рода решение уравнения теплопроводности для промороженной зоны имеет вид
![]() (2.37)
(2.37)
При х= hиз выражения (2.37) имеем
![]() (2.38)
(2.38)
Для глин и суглинков Т ≈ -1°С и а2 ≈ 0,003÷0,01 м /с.
На основании выражения (2.38) можно определить (приближенное) значение глубины промерзания грунта без учета теплоты фазового перехода «вода-лед». Истинное значение глубины промерзания будет во втолько раз меньше расчетного, во сколько теплота фазового перехода «вода-лед» в единице объема грунта больше теплоты охлаждения от температуры Т0 до Тв.
Задавшись допустимой глубиной промерзания и используя таблицы для определения функции erfc(u), можно по формуле (2.38) рассчитать время промораживания грунта на эту глубину.
Если суточные колебания температуры окружающей среды достигают 10°С, то на основании (2.38) можно показать, что
![]() ≈
1. (2.39)
≈
1. (2.39)
При этом время, по истечении которого наступит установившийся режим, будет примерно равно 1 ч.
В случае, когда суточные колебания температуры составляют 3-5°С,
![]() ≈0,1.
(2.40)
≈0,1.
(2.40)
Время наступления установившегося режима при этом будет равно примерно 10 ч.
Эти сравнения сделаны с тем расчетом, чтобы показать, что для решения задач по определению глубины и времени промораживания грунта функцию Т(у) можно считать постоянной величиной, равной минимальной отрицательной температуре на данные сутки.
