23

ПЕТРОЗАВОДСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

КОЛЬСКИЙ ФИЛИАЛ

Физико-энергетический факультет

Кафедра энергетики и электротехники

Физико-математические основы техники высоких напряжений

Методическая разработка

для студентов технических специальностей

Составитель: В.Н.Селиванов

Апатиты 2013

Оглавление

1. Погрешность результата численного решения задачи	3
2. Решение систем линейных уравнений	4
3. Численное решение алгебраических и трансцендентных уравнений	6
4. Приближенные вычисления определенных интегралов	12
5. Решение обыкновенных дифференциальных уравнений	14
Литература	18

1. Погрешность результата численного решения задачи Причины возникновения и классификация погрешности

Отклонение истинного решения от приближенного назовем погрешностью.

Решение задач всегда имеют погрешность, связанную со следующими причинами:

1) созданием математической модели (любая модель имеет свою степень точности);

2) получением исходных данных (т.к. являются "результатом измерений", следовательно, возникают измерительные погрешности);

3)использованием вычислительной техники (ошибки округления, возникающие из-за ограниченной разрядной сетки и ошибки, связанные с самими методами).

На рис. 1 и 2 показаны составляющие неустранимой и полной погрешности.

Рис. 1.

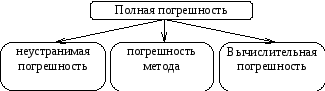
Рис. 2.

Неустранимую погрешность и погрешность метода необходимо контролировать, чтобы не осуществлять расчеты с избыточной точностью.

Характеристиками точности результата решения задачи являются абсолютная и относительная погрешности. Для технических задач 10 % - хорошая точность.

Определение. Если х - точное значение некоторого числа, х^* - приближенное, то абсолютной погрешностью приближения х^* назовем величину: , т.е. точное значение числа х заключено в границах.

Определение. Отношение абсолютной погрешности к абсолютному значению приближенной величины есть относительная погрешность (т.е. доля истинного значения): , при условии, что.

Пример: Найти абсолютную и относительную погрешности, если х=3.141592, а х^*=3.14.

Решение: .

Определение. Значащими цифрами числа называются все цифры в его записи, начиная с первой ненулевой слева.

Пример: У чисел подчеркнуты значащие цифры: 0.010087 и 0.0100870000.

Любое число можно представить в виде , где - основание системы счисления, n – некоторое целое число (старший десятичный разряд числа х), а_i – значащие цифры приближенного числа x.

Определение. Значащая цифра а_k считается верной, если имеет место неравенство: , где, в противном случае а_k - сомнительная цифра.

2. Решение систем линейных уравнений

В общем случае система линейных уравнений имеет вид

Чтобы эта система имела единственное решение, входящие в нее п уравнений должны быть линейно независимыми. Необходимым и достаточным условием этого является условие неравенства нулю определителя данной системы. Алгоритмы решения задач такого типа подразделяются на прямые и итерационные.

Наиболее распространенные прямые методы основаны на приведении системы уравнений к «треугольному» виду. При этом одно из уравнений содержит только одну неизвестную, а в каждом следующем добавляется еще по одной неизвестной. При счете вручную приведение к треугольному виду достигается сложением и вычитанием уравнений после умножения их на соответствующие постоянные множители. Выполняя эту процедуру вручную, нетрудно ошибиться, однако она позволяет построить удобный алгоритм численного решения на ЭВМ. Одним из используемых для этого методов является метод Гаусса. Применяя его, сначала нормируют первое уравнение, деля его коэффициенты на а₁₁. Затем первое уравнение умножают на первые коэффициенты a_i,1 всех других уравнений и последовательно вычитают из остальных уравнений. В результате первая переменная будет исключена из всех уравнений, кроме первого. На следующем этапе решения такая же процедура применяется к остальным п–1 уравнениям. В результате из оставшихся п–2 уравнений исключается вторая неизвестная. Всю процедуру повторяют до тех пор, пока после п шагов вся система не будет приведена к треугольному виду. Математически эту процедуру можно описать следующим образом.

На k-м шаге процесса исключения новые нормированные коэффициенты k-ro уравнения имеют вид

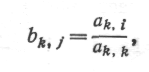
а новые коэффициенты в следующих уравнениях будут иметь вид

Выполняя эту процедуру, следует помнить, что коэффициенты нижестоящих уравнений a_i,j меняются на каждом шаге. Например, коэффициенты b_i,j на следующем шаге превращаются в коэффициенты a_i,j. Проиллюстрируем применение описанной процедуры на следующем простом примере.

Пусть методом исключения Гаусса требуется решить систему уравнений

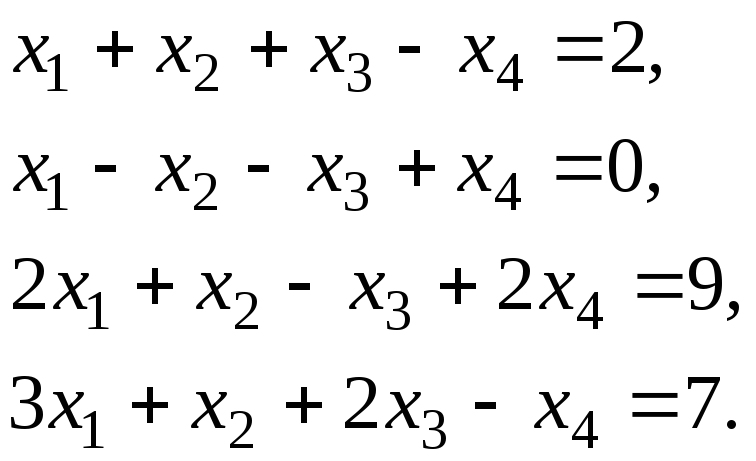
Для удобства уравнения обозначим буквами и будем выписывать только коэффициенты при неизвестных и свободные члены уравнений. Тогда исходная система примет вид:

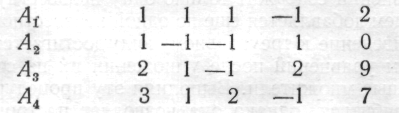
Исключая члены, содержащие x₁ получим

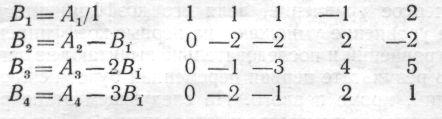
После исключения членов с x₂ имеем

Исключение членов с х₃ дает

Дойдя до последнего ряда, получим

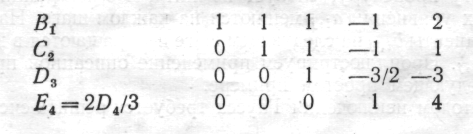
Возвращаясь к форме уравнений, получим

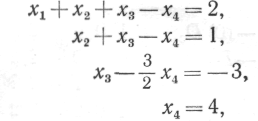
откуда, подставляя значение x₄ в 3-е уравнение, х₃ — во 2-е и т. д., находим решение системы уравнений

На этом примере хорошо видно, что желательно сделать нулевыми все элементы матрицы коэффициентов, стоящие вне главной диагонали. Последняя процедура называется приведением к диагональному виду и представляет собой усовершенствованную разновидность метода приведения к треугольному виду.