3. Построение ачх и фчх

Эти характеристики полностью определяют структуру частотного спектра выходного напряжения. Амплитудно-частотная характеристика отражает усилительные свойства электрической цепи. Фазо-частотная характеристика определяет фазовый сдвиг выходного напряжения относительно входного.

В комплексной форме (3) выделяем вещественную P(ω) и мнимуюQ(ω)части

Амплитудно-частотная характеристика:

(4)

Фазо-частотная характеристика

(5)

Где параметр φ^* подбирается так, чтобы обеспечить непрерывность функцииφ(ω) при том значенииω_к,при котором обращается в нуль знаменатель в аргументе арктангенса, т.е.

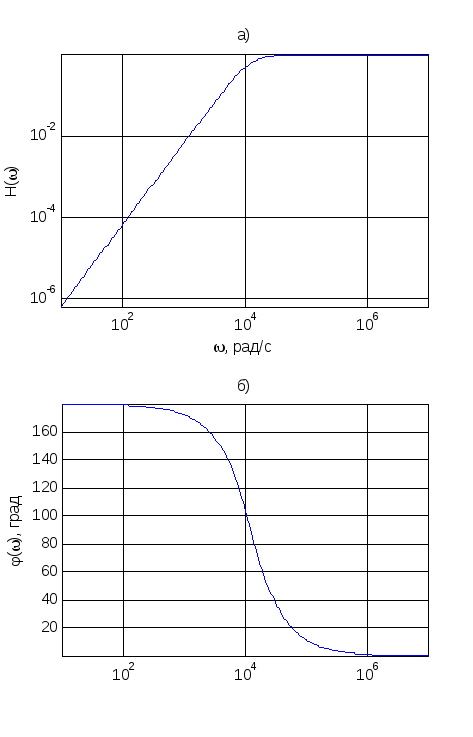
Рис. 6. Характеристики цепи: а – амплитудно-частотная; б–фазо-частотная

4. Определение устойчивости

Условие устойчивости состояния покоя электрической цепи заключается в том, что после прекращения действия внешних возмущений цепь возвращается в исходное состояние. Для этого необходимо, чтобы возникающие в цепи при нарушении состояния покоя переходные токи и напряжения были затухающими. Энергия переходного процесса преобразуется в активных сопротивлениях цепи в теплоту, которая отводится в окружающую среду. Достаточное условие устойчивости электрической цепи: если корни числителя – нули и корни знаменателя – полюса передаточной функции HU(p) = A(p)/B(p) имеют отрицательную вещественную часть, то цепь устойчива.

Bнашем случае имеется двукратный корень числителя (2),p=0, что является нейтральным условием по отношению к устойчивости. Приравняв нулю знаменатель (2) и решив полученное уравнение

,

найдем два комплексно-сопряжённых его корня:

. (6)

Это полюса передаточной функции. Отобразим положение полюсов и нулей фнкции на комплексной плоскости. Т.к. полюса (их отмечают крестиком) расположены в левой полуплоскости комплексной плоскости корней (рис. 7), это означает, что переходные процессы в цепи затухают и цепь устойчивая.

Рис.7. Полюса и нуль функции H_U(p) на комплексной плоскости

5. Определение реакции цепи на периодическое негармоническое входное воздействие

Фильтрующие свойства цепи во временной области проявляются в виде реакции цепи на периодическое несинусоидальное воздействие или воздействие более сложной формы. Разложение входного напряжения в бесконечный тригонометрический ряд Фурье имеет вид

Ограничим ряд Фурье первыми пятью гармониками.

Частоту внешнего воздействия подберем исходя из того условия, чтобы в диапазоне от ω₁до 9ω₁зависимостьH_U(ω) претерпевала существенное изменение. Для рассматриваемого варианта можно принятьf₁=1000 Гц,T₁=10^-3c. Амплитуду воздействия выберемU_m=1В.

У гармоник с нечётными номерами начальная фаза нулевая, с чётными – равная π. Занесём в таблицу характеристики первых пяти гармоник разложения входного сигнала:

№ гармоники	Цикл. частота, с-1	Амплитуда, В	Начальная фаза, рад
1
2
3
4
5

Построим амплитудный и фазовый частотные спектры входного воздействия. Амплитудный и фазовый спектры первых гармоник напряжения U₁(t) даны на рисунке:

a)б)

Рис.8. Амплитудный (а) и фазовый (б) частотные спектры входного воздействия.

Рис. 9. Первые гармоники входного напряжения (1-5) и их сумма (6)

Расчет и построение выходного напряжения. Сначала найдём реакцию цепи на каждую гармонику входного напряжения в отдельности. Результирующая реакция равна сумме составляющих реакций. Амплитуда n-й гармоники на выходе определяется выражением

,

а фаза – выражением

Вычисления по этим формулам сведены в таблицу:

№ гармоники n	Цикл. частота ωn,с-1	Амплитуда , В	Начальная фаза , град.
1	6,28·103	0,300	131,3
2	18,8·103	0,351	241,4
3	31,4·103	0,240	36,9
4	44,0·103	0,179	206,2
5	56,5·103	0,139	20,3

Построим амплитудный и фазовый частотные спектры выходной реакции.

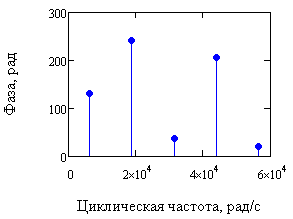
Рис. 10. Амплитудный и фазовый спектры по частоте для выходного сигнала.

Выведем на график пять первых гармоник выходного сигнала и их сумму, аппроксимирующую отклик цепи на периодически повторяющийся прямоугольный импульс, подаваемый на вход. На графике хорошо заметны искажения формы сигнала. Понизился и интегральный уровень сигнала, хотя пиковые значения по-прежнему достигают 1 вольта. Поэтому для более качественной аппроксимации не следует ограничиваться всего пятью гармониками, т.к. при увеличении частоты AЧXне спадает, а даже растёт, и вклад высоких гармоник существенен.

Рис. 11. Пять гармоник на выходе и их сумма