mex1

`ТИПОВОЙ РАСЧЕТ № 1

Вариант №1

1. Камень, брошенный с высоты h = 2,1 м под угломα = 45° к горизонту, падает на расстоянии S = 42м (по горизонтали) от места бросания. Найти начальную скорость камня, время полета и максимальную высоту подъема над уровнем Земли. Определить также радиусы кривизны траектории в верхней точке и в точке падения камня на Землю.

2.Шарик массой m , подвешенный на нити, имеющий длину , вращается в горизонтальной плоскости. Какова должна быть сила натяжения Т нити, чтобы радиус R окружности, по которой движется шарик, мог достигнуть величины

2 /5.

3.Момент инерции однородного шара относительно оси, проходящей через его центр, J = 2 / 5mR2 . Считая Землю однородным шаром, вычислите кинетическую энергию, обусловленную ее суточным вращением. Масса Землиm = 6i1024 кг, радиус R = 6.3i105 км.

Вариант № 2

1. По наклонной доске пустили катиться снизу вверх шарик. На расстоянии = 0,3 м от начальной точки движения шарик побывал дважды: через t1 =1с и

через t2 = 2с после начала движения. Определить начальную скорость и ускорение движения шарика, считая его постоянным.

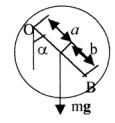
2.В установке, показанной на рисунке, массы тел равны m0 , m1 , m2 , массы блока и нитей пренебрежимо малы и трения в блоке нет. Полагая, что тело массыm0

опускается, найти его ускорение и натяжение нити, связывающей тела m1 , m2 ,

если коэффициенты трения между горизонтальной поверхностью и телами m1 , m2 одинаковы и равны k.

3. Тонкий однородный стержень длины =1м может свободно вращаться вокруг горизонтальной оси z, проходящей через точку O на стержне. Стержень отклонили от вертикали на уголα и отпустили. Определить для начального момента времени угловое ускорение ε и тангенциальное ускорение aτ

точки В на стержне. Вычисление произвести для следующих случаев:

1) a = 0,b = 2 / 3,α =π / 2; 2) a = / 3,b = ,α =π / 3; 3) a = / 4,b = / 2,α = 2π / 3;

Вариант № 3

1.Материальная точка начинает двигаться по окружности радиуса r =10см с постоянным касательным ускорением aτ =0.4м/с2. Через какой промежуток времени вектор ускорения а образует с вектором скорости v угол β , равный 60° и 80°? Какой путь пройдет за это время движущаяся точка?

2.В вагоне, движущимся горизонтально с ускорением α =2 м/с, висит на шнуре груз массы m=200г. Найти силу натяжения шнура и угол отклонения шнура от вертикали.

3.Однородный диск радиуса R=10 см может свободно вращаться вокруг горизонтальной оси, перпендикулярной плоскости диска и проходящей через точку О расположенную на нем. Диск отклонили на угол а, и отпустили.

произвести для следующих случаев:

1)a = R,b = R / 2,α =π / 2

2)a = R / 2,b = R,α =π / 6

3)a = 2R / 3,b = 2R / 3,α = 2π / 3

Вариант № 4

1.Частица движется в плоскости ху со скоростью v = ai +bxj , где i и j - орты

осей х и у соответственно, a и b - постоянные. В начальный момент частица находилась в точке х=у= 0. Найти: а) уравнение траектории частицы у(x); б) радиус кривизны траектории в зависимости от координаты x.

2.На гладкой наклонной плоскости, образующей угол α =30° с горизонту, находится тело массой m=50кг, на которое действует горизонтально направленная сила F=294Н. Найти ускорение тела и силуFН. Д. , с которой тело давит на плоскость (тело движется вниз).

3.На сплошной однородный цилиндр массы m2 =10 кг намотан шнур, к концу которого привязан груз массы m1 =2 кг. Определить ускорение а груза и силу F натяжения шнура. Массой шнура и трением пренебречь.

Вариант № 5

1.Воздушный шар начинает подниматься с поверхности Земли. Скорость его подъема постоянна и равна v0 . Благодаря ветру шар приобретает горизонтальную компоненту скоростиvx = ay , где а - постоянная, у - высота от поверхности Земли. Найти: а) величину сноса шара в зависимости от высоты подъема х(у); б) полное, тангенциальное и нормальное ускорения шара.

2.На экваторе некоторой планеты тело весит вдвое меньше, чем на полюсе. Плотность вещества этой планеты 3 г/см3. Определить период вращения планеты вокруг своей оси.

3.На барабан радиусом R=20 см, момент инерции JZ которого равен 0,1 кгм2, намотан шнур, к концу которого привязан груз массы m=0,5 кг. До начала вращения барабана высота h груза над полом равна 1 м. Найти: 1) времяτ , в течение которого груз опуститься до пола; 2) силу F натяжения нити. Массой шнура и трением пренебречь.

Вариант № 6

1.Материальная точка движется в плоскости ху по закону: x = at, y =bt −ct2 , где a=50,0 см/с, b=200 см/с, с=25,0 см/с2. Найти в момент времени t =3,00с: а) скорость и ускорение точки; б) угол между векторами скорости v и ускорения

а.

2.Определить плотность планеты, продолжительность суток на которой равна Т, если известно, что на экваторе планеты тела невесомы.

3.Два тела массами m1 =0.25 кг и m2 =0.15 кг связаны тонкой нитью, переброшенной через блок. Блок укреплен на краю горизонтального стола, по поверхности которого скользит тело массойm1 . С каким ускорением а движутся тела и каковы силы F1 иF2 натяжения нити (по обе стороны от блока)? Коэффициент трения k тела о поверхность стола равен 0,2. Масса m блока равна 0,1 кг и её можно считать равномерно распределённой по ободу. Массой веревки и трением в подшипниках оси блока пренебречь.

Вариант № 7

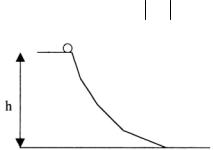
1.На горе с углом наклонаα к горизонту бросают мяч с начальной скоростью v0 перпендикулярно склону горы. Найти время полета мяча. На каком

расстоянии от точки бросания упадет мяч?

2.Найти среднюю плотность ρ планеты, если на экваторе показания

динамометра, к которому подвешено тело на 10% меньше, чем на полюсе. Продолжительность суток на планете τ =6 ч.

3.Через блок, имеющий форму диска, перекинут шнур. К концу шнура привязали грузики массами m1 =100 г и m2 =150 г. С каким ускорением а будут двигаться грузики и каковы силы F1 иF2 натяжения нити (по обе стороны от блока), если масса m блока равна 200г? Трение при вращении блока ничтожно мало. Массой шнура пренебречь.

Вариант № 8

1.За промежуток времени τ =10,0с частица прошла половину окружности радиусом R= 160см с постоянным тангенциальным ускорением. Вычислить за это время: а) средний модуль скоростиv ; б) модуль среднего вектора полного ускорения a .

2.Через блок, прикрепленный к потолку кабины лифта, перекинута нить, к концам которой привязаны грузыm1 =0,5кг иm2 =0,6кг. Найти силу давления

блока на ось при движении грузов в двух случаях: лифт поднимается равномерно и с ускорением a0 =1,2 м/с2. Масса блока пренебрежимо мала.

Трением в оси пренебречь.

3. Найти моменты инерцииJZ двух атомных молекул типов A2 и АВ относительно оси,

проходящей через центр инерции С молекулы перпендикулярно прямой, соединяющей ядра атомов. Вычисление произвести для следующих молекул: 1)H2 2)J2 3)HJ 4)NO

межатомные расстояния d:

1)0.741 10−10 м2)2.67 10−10 м3)1.61 10−10 м4)1.15 10−10 м

Вариант № 9

1.Тело брошено вертикально вверх со скоростью 20 м/с. Через сколько времени от начала движения оно упадет обратно? На какую высоту оно поднимется? Найдите перемещение и путь тела за 4 секунды движения.

2.Шарик, подвешенный на нити, имеющий длинуl , описывает окружность в горизонтальной плоскости. Нить составляет с вертикалью угол α . Найти период τ обращения шарика, если маятник находится в лифте, движущимся с постоянным ускорениемa < g , направленным вниз.

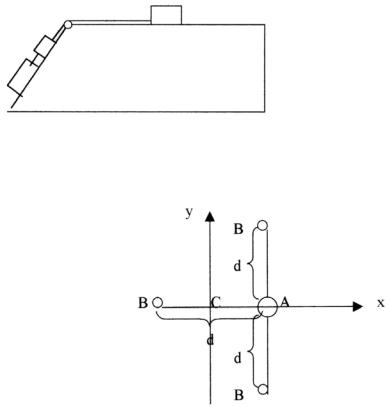
3.Определите моменты инерции Jz , J y , Jx трёх атомных молекул типа

AB2 относительно осей х, у, z проходящих через центры инерции С молекулы.

Положение осей х и у указаны на рисунке. Ось z перпендикулярна плоскости ху. Вычисления выполнить для следующих молекул: 1) H2O ; 2) H2S ; 3) SO2 ;

4) CO2 . Межъядерные расстояние d (d = AB) и валентные углыα : 1) 0.97i10−10 м,104.5°; 2)1.35i10−10 м,92.3°; 3)1.45i10−10 м,124°;

4) 1.13i10−10 м,180°.

Вариант № 10

1.Тело бросили под углом α к горизонту с начальной скоростьюv0 . Пренебрегая сопротивлением воздуха, найти:а) время полета; б) максимальную высоту подъема и горизонтальную дальность полета; в) уравнение траектории у(х), где у и х - перемещения тела по вертикали и горизонтали соответственно; г) радиусы кривизны начала и вершины траектории.

2.Наклонная доска, составляющая с горизонтом угол 60°, приставлена к горизонтальному столу. Три груза массой по 1 кг каждый соединены невесомой нерастяжимой нитью, перекинутой через неподвижный и невесомый блок, и могут перемещаться соответственно по доске и столу. Найти силу натяжения нити и ускорение системы, если коэффициент трения тел о поверхности доски и стола одинаков и равен 0,3.

3.Вычислить моменты инерцииJz , J y , Jx четырёх атомной Т - образной

молекулы ClF3 относительно осей x,y,z, проходящей через центр инерции С молекулы. Положение осей х и у указаны на рисунке. Ось z перпендикулярна плоскости ху. Межъядерные расстояния d считать известными: 2.33i10−10 м.

Вариант № 11

1. С башни высотой Н = 25м горизонтально брошен камень со скоростью

v0 =10м/ с . На каком расстоянии от основания башни он упадет? Какова его

начальная скорость? Какой угол образует вектор конечной скорости с горизонтом?

2.Груз массы m = 200г, привязанный к нити длиной l = 40см, вращают в горизонтальной плоскости с постоянной скоростью так, что нить описывает коническую поверхность. При этом угол отклонения нити от вертикали

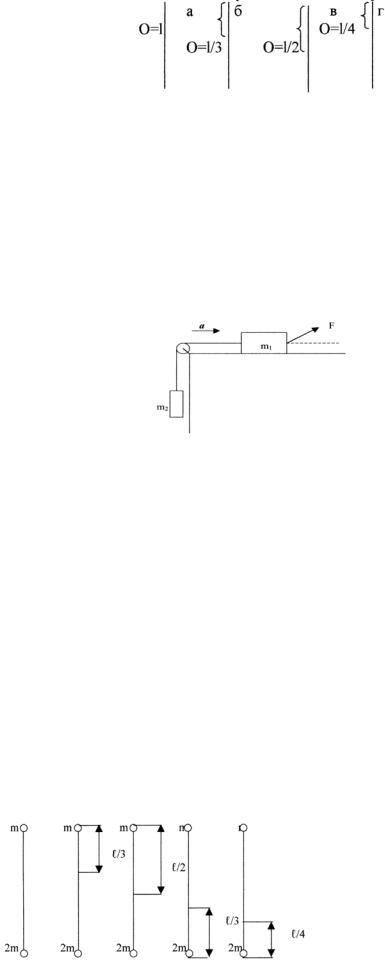
α =37°. Найти угловую скорость со вращения груза и силу натяжения нити. 3. Вычислить моменты инерции Iz тонкого однородного стержня длинной =1 м

массой m =1.2 кг относительно оси z, перпендикулярной стержню и проходящей через точку О, лежащую на оси стержня. Вычисление выполнить для случаев а, б, в, г, изображенных на рисунке:

Вариант № 12

1. Два тела бросили одновременно: одно - вертикально вверх со скоростью v1 = 25.0м/ с, другое - под углом α =37°к горизонту со скоростью

v2 =30,0м/ с. Пренебрегая сопротивлением воздуха, найти их относительную скорость во время движения.

2.Определить ускорение тел в системе, показанной на рисунке. Коэффициент трения между телом m1 и плоскостьюμ = 0.1 . Массой блока и нити можно пренебречь. Нить нерастяжима. Масса грузовm1 =1.5кг, m2 = 0,5кг , сила F образует уголα =30° к горизонту, а ее модуль равен 10 H.

3.Вентилятор вращается с частотой 900 об/мин. После выключения вентилятор, вращаясь равно замедленно, сделал до остановки N=75 оборотов. Работа сил торможения равна А = 44Дж. Найти: 1) момент инерции J вентилятора; 2)

момент сил торможения М.

Вариант № 13

1.Тело брошено с начальной скоростью под углом к горизонту. Найти скорость v0 и уголα , если известно, что максимальная высота подъема тела

hmax равна 5м и радиус кривизны траектории тела в верхней точке траектории R = 5м.

2.Доска массой М может двигаться без трения по наклонной плоскости с углом наклона α к горизонту. В каком направлении и с каким ускорением должна

бежать по доске собака массой m чтобы доска не соскальзывала с наклонной плоскости?

3. На концах тонкого однородного стержня длинны и массы 3m прикреплены маленькие шарики массой m и2m . Определить момент инерции

Jz относительно оси z, перпендикулярной стержню и проходящей через точку

О, лежащую на оси стержня. Вычисления выполнить для случаев а, б, в, г, д, изображенных на рисунке. При расчетах принять =1 м, m =0.1 кг.

Вариант № 14

1.Шкив радиусом 20 см приводится во вращение в вертикальной плоскости грузом, подвешенным на нити, постепенно сматывающейся со шкива. В

начальный момент груз был неподвижен, а затем стал опускаться с ускорением 2 м/с2. Найдите угловую скорость шкива в тот момент, когда груз опустится на 1м. Определите величину и направление ускорения произвольной точки шкива в этот момент.

2.На наклонной плоскости с углом наклона а неподвижно лежит кубик причем коэффициент трения между кубиком и плоскостью равенμ =tgα . Наклонная

плоскость движется с ускорением а в направлении указанном стрелкой. При каком минимальном значении этого ускорения кубик начнет соскальзывать?

3.Определить момент инерции тонкого однородного кольца радиусом R=10см и массой m=0.1кг относительно оси: 1) перпендикулярной плоскости кольца и проходящей через его образующую; 2) лежащей в плоскости кольца и проходящей через его центр; 3) лежащей в плоскости кольца и касательной к окружности.

Вариант № 15

1.Тело бросают под углом 30° к горизонту с начальной скоростью 14 м/с. На расстоянии 11м от точки бросания тело упруго ударяется о вертикальную стенку. На каком расстоянии от стенки оно упадет на землю?

2.На подставке лежит тело, подвешенное к потолку с помощью пружины. В начальный момент времени пружина недеформированная. Подставку начинают опускать вниз с ускорением . Через какое время тело оторвется от подставки. Коэффициент жесткости пружины равен k, масса тела - m.

3.Определить момент инерции Jz однородного диска радиуса R=20см и массой 5 кг, относительно оси z, перпендикулярной плоскости диска в двух случаях: 1) ось z проходит через середину радиуса; 2) ось z совпадает с образующей диска.

Вариант № 16

1.Материальная точка начинает двигаться без начальной скорости по окружности радиусом К=20см с постоянным тангенциальным ускорением

aτ =5 см/с2. Через какое число оборотов после начала движения нормальное ускорение точки станет равным тангенциальному?

2. Шарик массой m = 0.2 кг. скатывается по желобу с высоты h=2м. Начальная скорость v0 =0. Найти изменение импульса p1 шарика и импульс p2 полученный желобом при движения шарика.

3.К ободу однородного диска радиусом R=0.2м приложена постоянная касательная сила F=98.1H. При вращении на диск действует момент силы

трения M тр =0.5кгм. Найти вес диска, если известно, что диск вращается с постоянным угловым ускорением 100рад/с2.

Вариант № 17

1. Материальная точка движется по окружности со скоростью v = at,

гдеa =0.50м/ с. Найти ее полное ускорение в момент, когда она сделает n=0,10 оборота после начала движения.

2.Тело массой m=2 кг движется поступательно под действием некоторой силы согласно уравнению x=A+Bt+Ct2+Dt3, где С=1 м/с2 , D=- 0.2 м/с3. Найти значение F1 и F2 этой силы в моменты времени t1 =2c, t2 =5c. В какой момент времени t сила равна нулю?

3.Однородный стержень длиною 1м и весом 0,5кг вращается в вертикальной плоскости вокруг горизонтальной оси, и проходящей через середину стержня. С каким угловым ускорением вращается стержень, если вращающий момент

равен9.81 10−2 Hм?

Вариант № 18

1. Частица движется по дуге окружности радиусом R по закону = a sinωt , где - смещение из начального положения, отсчитываемое вдоль дуги, а и ω - постоянные. Полагая R=1,00м, a=0,80м и ω =2,00 рад/с, найти полное ускорение частицы в точках =0 и ± а.

2.Тело, имеющее постоянную массу, до торможения двигалось равномерно, а в

момент остановки тормозящая сила достигла значения FK=-40H. Определить тормозящую силу F через время t=3c после начала торможения, если тормозной путь в зависимости от времени изменялся по закону S=At+Bt3,

где А=12м/с и В=-0.25 м/с3.

3.Однородный диск радиусом 0,2м и весом 5кг вращается вокруг оси,

проходящей через его центр. Зависимость угловой скорости вращения диска от времени даётся уравнением ω = А + Bt, где В=8 рад/с2. Найти величину касательной силы, приложенной к ободу диска. Трением пренебречь.

Вариант № 19

1. Твердое тело вращается вокруг неподвижной оси по закону ϕ = at −br3 ,

где a =6,0 рад/с, b=2,0 рад/с3. Найти: а) среднее значение модулей угловой скорости ω и углового ускорения ε за промежуток времени от

t =0 до остановки; б) угловое ускорение ε1 в момент, когда тело остановится.

2.Два шарика падают в воздухе. Шарики (сплошные) сделаны из одного материала, но диаметр одного из шариков вдвое больше, чем у другого. В каком соотношении будут находиться скорости шариков при установившемся движении? Считать, что сила сопротивления воздуха пропорциональна площади поперечного сечения движущегося тела и квадратично зависит от скорости движения тела.

3.Маховик, момент инерции которого равен 63,6 кг.м2, вращается с постоянной угловой скоростью 31,4 рад/с. Найти тормозящий момент М, под действием которого маховик останавливается через 20с.

Вариант № 20

1. Тело брошено с башни под углом 30° к горизонту со скоростью 10м/с. Каково кратчайшее расстояние между местом бросания и местом нахождения тела спустя 3с после бросания.

2.Парашютист, масса которого m=80кг совершает прыжок с парашютом. Считая, что сила сопротивления воздуха пропорциональна скорости движения, определить, через какой промежуток времени τ скорость парашютиста будет равна 0.9 от скорости установившегося движения. Коэффициент сопротивления k принять равным 10 кг/с. Начальная скорость парашютиста равна 0.

3.К ободу колеса, имеющего форму диска, радиусом 0,5м и массой 50кг

приложена касательная сила 10H. Найти: 1) угловое ускорение колеса; 2) через сколько времени после начала действия силы колесо будет иметь скорость, соответствующую 100 об/с.

Вариант № 21

1.Твердое тело начинает вращаться вокруг неподвижной оси с угловым ускорениемε = at , где a = 2.0 10−2 рад/с3. Через сколько времени после начала вращения вектор полного ускорения произвольной точки тела будет составлять угол а=60° с ее вектором скорости?

2.Снаряд массы m=10кг выпущен из зенитного орудия вертикально вверх со скоростью v0 =800м/с. Считая силу сопротивления воздуха пропорциональной скорости, определить время τ подъема снаряда до высшей точки и высоту подъема. Коэффициент сопротивления k принять равным 0.26 кг/с.

3.Маховик радиусом 0,2м и массой 10кг соединен с мотором при помощи приводного ремня. Натяжение ремня, идущего без скольжения, постоянно и равно 14,7 Н. Какое число оборотов в секунду будет делать маховик через время 10с после начала движения? Маховик считать однородным диском. Трением пренебречь.

Вариант № 22

1.На берегу высотой 20м над уровнем моря под углом 30° к горизонту установлено орудие. Определить высоту подъема и дальность полета снаряда, если скорость вылета снаряда из ствола орудия 600 м/с, а сопротивление воздуха уменьшает дальность полета в 4 раза.

2.Катер трогается с места и в течении времени т равным 10с развивает скорость

v=4м/с. Определить силу тяги F мотора, считая ее постоянной. Сила

сопротивления Fc движению принять изменяющейся пропорционально скорости и коэффициент сопротивления k равным 100 кг/с. Масса m катера

равна 2 103 кг.

3.Маховое колесо, имеющее момент инерции 245 кгм, вращается, делая 20 об/с, через минуту после того как на колесо перестал действовать вращающий момент, оно остановилось. Найти: 1) момент силы трения; 2) число оборотов, которое сделало колесо до полной остановки после прекращения действия сил.

Вариант № 23

1.По дуге окружности радиусом R=5м движется точка. В некоторый момент времени нормальное ускорение точки ап= 2,5 м/с2. В этот момент времени векторы полного и нормального ускорений образуют угол γ =60° . Найти скорость v и тангенциальное ускорение am точки.

2.Доска массой M=400г движется по поверхности стола. Коэффициент трения между поверхностью стола и доской μ =0.2. В некоторый момент времени,

когда скорость доски была v0 =0.5 м/с, на нее осторожно опустили брусок массой m=200г. Определить путь, который пройдет брусок по доске, пока он не остановится относительно доски. Коэффициент трения между бруском и доской μ1 =0.3 поверхность стола считать горизонтальной.

3.Две гири весом 2кг и 1кг соединены нитью и перекинуты через блок весом 1кг. Найти: 1) ускорение, с которым движутся гири; 2) натяжение нитей, к которым подвешены гирьки. Блок считать однородным диском. Трением пренебречь.

Вариант № 24

1.Шар радиусом R= 10,0см начинает скатываться без скольжения по наклонной плоскости так, что его центр движется с постоянным ускорением a=2,50 см/с2. Найти через t=2,00 с после начала движения скорость точек А, В и С,

показанных на рисунке.

2.Четыре одинаковых груза массой m=2кг каждый, связанные невесомыми нерастяжимыми нитями, движутся по горизонтальной поверхности под действием силы F=10H, направленной под углом α =30° к горизонту. Коэффициент трения всех грузов о поверхность одинаков и равен μ =0.1. Найти силы натяжения всех нитей и ускорение грузов.

3.На барабан массой 9 кг намотан шнур к концу которого привязан груз массой 2кг. Найти ускорение груза. Барабан считать однородным цилиндром. Трением пренебречь.