
0,65 |
0,7920 |
1,80 |
0,0032 |
0,70 |
0,7112 |
1,90 |
0,0015 |
0,75 |
0,6272 |
2,00 |
0,0007 |
0,80 |
0,5441 |
2,10 |
0,0003 |
0,85 |
0,4653 |
2,20 |
0,0001 |
0,90 |
0,3927 |
2,30 |
0,0001 |
0,95 |
0,3275 |
2,40 |
00000 |
1,00 |
0,2700 |
2,50 |
00000 |
1) критерий Романовского (автор – В.И. Романовский) (Кр):
Кр = χ22-vv , где v – число степеней свободы. Если Кр<3, то
расхождения между распределениями случайны (то есть согласуются). Напротив, если Кр>3, то расхождения между распределениями не случайны, и модель данного теоретического распределения не годится для описания соответствующих эмпирических данных. Критерий Романовского наиболее удобен, поскольку здесь не нужны вспомогательные таблицы. Рассчитаем критерий Романовского для нашего примера:
Кр = |
|
χ2 -v |
= |
|
12,85 -5 |
|
= |
7,85 |
=2,48 . |
|
|
|
|
|
|
|
|
|
|
|
|
3,16 |
|
2v |
2 ×5 |
|
|
|
|
|
|
|
|
|
|
Поскольку полученное значение меньше трех, постольку можно утверждать, что эмпирическое и теоретическое распределения согласованы.
3) критерий Ястремского (автор – Б.С. Ястремский) (L):
|
|
|
|
|
|
|
|
å |
( fi - fT )2 |
- K |
|
|
|
i |
, где K – число вариантов или групп, N – число |
L = |
|
N × p ×q |
|
|
|
|
|
|
|
2 × K +4 ×Q |
|
|
наблюдений (объем совокупности); pq – дисперсия альтернативного признака: σ2 = pq , где p – доля единиц в совокупности, обладающих данным признаком, q – доля единиц в совокупности, не обладающих данным признаком; Q – принимает значение 0,6 при числе вариантов или групп от 8 до 20. Если L>3, то эмпирическое и теоретическое распределение согласованы.
В продвинутых программных пакетах такие критерии обычно вычисляются автоматически (достаточно указать соответствующий критерий).
Ответ: можно утверждать, что с вероятностью 0,95 (95%) распределение коэффициентов преступности (относительных уровней преступности) по субъектам Российской Федерации в 2010 году подчинялось нормальному, с параметрами: x =1792 ;σ = 530 .
Ниже представлены графики такого распределения:
1)Функция плотности распределения (дифференциальная функция) f(x) преступности по субъектам РФ в 2010 году построенная в программе Excel:
2)Интегральная функция распределения F(x) преступности по субъектам РФ в 2010 году построенная в программе Excel:
Таблица. Значения F(x) и f(x).
|
|
|
X, |
|
|
шт. |
F(x) |
f(x) |
|
|
|
|
0,00070 |
|
100 |
5 |
4,60811E-06 |
|
|
|
|
0,00133 |
|
200 |
3 |
8,26779E-06 |
|
|
|
|
0,00243 |
|
300 |
8 |
1,43151E-05 |
|
|
|
|
0,00431 |
|
400 |
4 |
2,39189E-05 |
|
|
|
500 |
0,00739 |
3,85678E-05 |
|
|
|
|
0,01225 |
|
600 |
4 |
6,00134E-05 |
|
|
|
|
0,01968 |
|
700 |
1 |
9,01178E-05 |
|
|
|
|
0,03062 |
|
800 |
4 |
0,000130591 |
|
|
|
|
0,04618 |
|
900 |
6 |
0,000182622 |
|
|
|
|
0,06754 |
|
1000 |
3 |
0,000246453 |
|
|
|
|
0,09583 |
|
1100 |
4 |
0,000320961 |
|
|
|
|
0,13200 |
|
1200 |
1 |
0,000403377 |
|
|
|
|
|
|
|
0,17662 |
|
1300 |
5 |
0,000489225 |
|
|
|
|
0,22976 |
|
1400 |
4 |
0,000572592 |
|
|
|
|
0,29083 |
|
1500 |
6 |
0,000646728 |
|
|
|
|
0,35857 |
|
1600 |
7 |
0,000704915 |
|
|
|
|
0,43109 |
|
1700 |
6 |
0,000741466 |
|
|
|
|
0,50602 |
|
1800 |
2 |
0,000752636 |
|
|
|
|
0,58073 |
|
1900 |
5 |
0,000737255 |
|
|
|
|
0,65263 |
|
2000 |
8 |
0,00069693 |
|
|
|
|
0,71942 |
|
2100 |
4 |
0,000635771 |
|
|
|
|
0,77929 |
|
2200 |
4 |
0,000559694 |
|
|
|
|
0,83109 |
|
2300 |
2 |
0,000475489 |
|
|
|
|
0,87434 |
|
2400 |
4 |
0,000389824 |
|
|
|
|
0,90920 |
|
2500 |
1 |
0,000308416 |
|
|
|
|
0,93631 |
|
2600 |
2 |
0,000235474 |
|
|
|
|
0,95666 |
|
2700 |
3 |
0,000173496 |
|
|
|
|
0,97140 |
|
2800 |
7 |
0,00012336 |
|
|
|
|
0,98171 |
|
2900 |
7 |
8,46446E-05 |
|
|
|
|
0,98867 |
|
3000 |
4 |
5,60484E-05 |
|
|
|
Ниже представлена гистограмма частот распределения коэффициентов преступности по субъектам Российской Федерации в 2010 году, аппроксимированная кривой нормального распределения, построенная в ППП Statistica. Видно, что
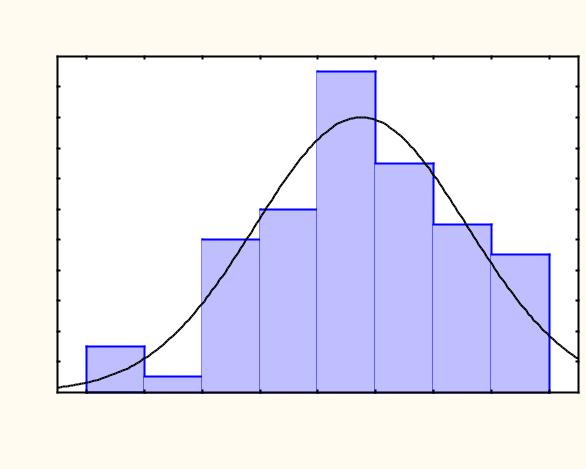
эмпирическое распределение частот вполне укладывается под |
кривой нормального распределения. |
|
|
|
|
|
Г и с т о г р а м м а ( H i s t o g r a m ( S p r e a d s h e e t 1 1 v * 8 2 c ) |
|
|
2 |
2 |
V a r 1 = 8 2 * 3 0 3 , 2 5 * n o r m a l ( x ; 1 7 9 2 , 3 2 9 3 ; 5 5 0 , 5 9 4 7 ) |
|
|
|
|
|
|
|
|
2 |
0 |
|
|
|
|
|
|
1 |
8 |
|
|
|
|
|
|
1 |
6 |
|
|
|
|
|
Частота |
1 |
4 |
|
|
|
|
|
1 |
2 |
|
|
|
|
|
1 |
0 |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
0 |
3 6 1 , 0 0 |
9 6 7 ,5 0 |
1 5 7 4 ,0 0 |
2 1 8 0 ,5 0 |
2 7 8 7 ,0 0 |
|
|
|
6 6 4 , 2 5 |
1 2 7 0 ,7 5 |
1 8 7 7 , 2 5 |
2 4 8 3 ,7 5 |
|
Х , ш т .
Можно обратить внимание, что стандартное отклонение в данном случае равно не 530, а 550, поскольку рассчитано непосредственно по всем наблюдениям. Мы же брали среднее взвешенное по серединам интервалов, получив в итоге значение стандартного отклонения не 550, а 530.
Найдем моду для распределения коэффициентов преступности по субъектам Российской Федерации для 2010 года:
для интервального ряда с равными интервалами:
|
Мо = xk −1 |
+hk × |
|
|
|
fk |
- fk −1 |
|
|
|
, где Мо – мода, хk-1 – нижняя |
|
( f |
k |
- f |
k −1 |
) +( f |
k |
- f |
k +1 |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
граница модального интервала, hk – длина модального интервала, fk- 1, fk и fk+1 – частота интервала предшествующего модальному, модального и следующего за модальным.
Мо =1561 +300 × |
21 −13 |
=1702 |
, из чего следует, что |
(21 -13) +(21 -12) |
наиболее типичным для субъектов Российской Федерации является коэффициент преступности, колеблющийся около 1702 преступлений на 100 тысяч человек. Видно, что мода немного меньше среднего значения (1792).
На практике существуют различные способы диагностики нормального распределения (о некоторых из них мы еще поговорим в следующем параграфе). Одним из наиболее простых и эффективных способов распознания нормального распределения является использование графика на нормальной вероятностной бумаге (или просто: вероятностной бумаге). Вероятностная бумага
– это бумага с линейной разметкой вдоль оси абсцисс и значениями вероятности в процентах от 0,1% до 99.99% по оси ординат. Замечательным свойством такой бумаги является то, что нормальное распределение на ней представляется прямой линией, где независимой переменной выступают верхние границы интервалов распределения, а зависимой накопленные частоты от значений границ интервалов. Если эмпирическое распределение
является нормальным, то его значения ложатся на прямую линию или близко к ней. Напротив, чем дальше точки эмпирического распределения ложатся от прямой линии (линии нормального распределения) тем меньше вероятность того, что данное эмпирическое распределение является нормальным. С помощью вероятностной бумаги можно найти среднее значение и стандартное отклонение соответствующего эмпирического распределения. Для данных с нормальным распределением площадь под нормированной кривой нормального распределения (табулирована) и величина z для единицы (то есть одного единичного отклонения) может быть получена из соответствующей таблицы стандартного распределения. При использовании вероятностной бумаги среднее квадратическое отклонение находится из выражения:
|
(G84% ) − (G16% ) |
, где G84% - значение переменной (x) для 84% |
|
2 |
|
|
накопленной частоты, G16% - значение переменной (x) для 16% 78

накопленной частоты. Среднее значение переменной (х – по оси абсцисс) соответствует значению 50% накопленной частоты (G - ордината). То есть мы находим на оси ординат значение накопленной частоты соответствующее 50%, проводим от этой точки горизонтальную линию до прямой нормального распределения и проводим от неё вертикальную линию до пересечения с осью абсцисс – это и будет среднее значение (х) для исследуемого эмпирического распределения. Далее на оси ординат находим значение для накопленной частоты в процентах, соответствующее 84%, проводим от этой точки горизонтальную линию до прямой нормального распределения и опускаем линию вниз до пересечения с осью абсцисс – определяем значение х соответствующее 84% накопленной частоты. Ту же процедуру выполняем и для 16%. Затем из значения х, соответствующего 84%, вычитаем значение х, соответствующее 16%, и полученное число делим на два, определяя среднее квадратическое отклонение. Нужно отметить, что в отечественной и зарубежной математической литературе данный метод описывается довольно редко. Подробно с решением примера на нормальной вероятностной бумаге можно ознакомиться в работе Джона Бёрда. 14 В настоящее время «вероятностная бумага» реализована в различных вариациях в компьютерных программах. Ниже приводится один из возможных вариантов выполненный в ППП
Statistica для данных о распределении преступности по субъектам РФ в 2010 году. По оси абсцисс здесь расположены значения переменной (х), а по оси ординат – ожидаемое нормальное распределение (expected normal value).
14 Бёрд Дж. Инженерная математика: Карманный справочник/Пер с англ. – М.: Издательский дом «Додэка-ХХI», 2008. С.469-471.

|
3 |
N |
o r m |
a l P |
r o b |
a |
b |
ilit y |
P lo t |
o f |
V a |
r 1 |
( |
1 |
v * 8 2 |
c ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Normal Value |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Expected |
- 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- 32 0 0 |
6 0 0 |
|
1 0 0 0 |
|
|
|
1 4 0 0 |
|
1 8 0 0 |
|
|
|
2 2 0 0 |
|
2 6 0 0 |
3 0 0 0 |
|
4 0 0 |
|
8 0 0 |
|
1 2 0 0 |
|
1 6 0 0 |
|
|
2 0 0 0 |
|
2 4 0 0 |
|
2 8 0 0 |
|
|
|
|
|
|
|
O b s e r v e d V a lu e |
|
|
|
|
|
|
В целом видно, что точки распределения неплохо ложатся на линию нормального распределения (за исключением хвостов).
Таким образом, подводя итог решения задачи о распределении преступности по субъектам Российской Федерации в 2010 году, можно утверждать, что она распределяется по закону Гаусса (закону нормального распределения) с параметрами распределения:
μ = х =1792 , σ = 530 . Наиболее типичным для российских регионов в этом году было 1702 преступления на 100 тысяч человек (мода равна 1702), что ниже среднего значения.
Пример № 2.
Дано: в ходе полевого криминологического наблюдения была составлена таблица числа заявлений об особо тяжких преступлениях, поступающих в УВД за одни дежурные сутки (графы №1 и №2 таблицы №1).
Требуется: 1) проверить, подчиняется ли распределение числа заявлений об особо тяжких преступлениях, поступающих в
дежурную часть УВД, закону Пуассона; 2) если подчиняется, то вычислить параметр данного распределения и измерить его теоретические частоты; 3) построить график зависимости p(у) от y; 4) рассчитать вероятности поступления в УВД 0, 1, 2, 3, 4 и 5 заявлений.
Решение:
Таблица №1. Данные к задаче №1 (графы №1 и №2) и
фрагмент решения (графы №3-№5) |
|
|
Число |
|
|
|
|
|
|
заявлений |
об |
|
|
|
|
особо |
тяжких |
Количество |
yi∙mi |
|
m΄ |
преступлениях |
дежурных |
( yi - y)2 × mi |
, поступающих |
суток |
|
|
|
в |
дежурную |
(mi) |
|
|
|
часть |
УВД |
за |
|
|
|
|
сутки |
(yi) |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
177 |
0 |
|
99,56 |
172 |
|
1 |
|
|
123 |
123 |
|
7,69 |
129 |
|
2 |
|
|
49 |
98 |
|
76,56 |
48 |
|
3 |
|
|
12 |
36 |
|
60,75 |
12 |
|
4 |
|
|
3 |
12 |
|
31,69 |
2 |
|
5 |
|
|
1 |
5 |
|
18,06 |
1 |
|
ВСЕГО |
|
|
365 |
274 |
|
294,31 |
365 |
|
|
5 |
|
|
5 |
|
|
|
|
|
λ= у = |
å yimi |
= |
274 =0,75 |
σ 2 = |
å(yi - y)2 × mi |
|
= 294,31 |
=0,8 |
|
i=1 |
i=1 |
|
|
|
5 |
|
5 |
|
|
|
åmi |
|
365 |
|
|
åmi |
365 |
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
i=1 |
|
|
|
|
Поскольку |
y ≈σ2 , можно полагать, что распределение числа |
заявлений об особо тяжких преступлениях, поступающих в дежурную часть УВД, подчиняется закону Пуассона с параметром λ=0,75, а далее это предположение (гипотезу) нужно будет

k |
(mi − mi′) |
2 |
|
проверить с помощью критерия согласия Пирсона χ2=å |
|
, |
mi′ |
|
i=1 |
|
|
где k – число пар эмпирических и теоретических частот, mi – эмпирическая частота, mi′ - теоретическая частота. Число степеней свободы для распределения Пирсона: df=k-2, поскольку при построении частот используются две ограничивающие связи: y и
k |
|
оценки |
статистической значимости различий |
åmi . Для |
i=1 |
|
|
|
|
|
эмпирического и теоретического распределений χрасч |
2 сравнивают с |
χтабл |
2 . Если |
χрасч |
2 > χтабл |
2 , то при заданном уровне значимости α |
(обычно принимают α=0,1 (р=0,9); 0,05 (р=0,95); 0,01 (р=0,99)15 и соответствующем числе степеней свободы гипотеза H0 о несущественности расхождений отклоняется и принимается альтернативная гипотеза H1 о наличии существенных различий между теоретическим и эмпирическим распределениями. Напротив, если χрасч 2 ≤ χтабл 2 , то принимается гипотеза H0 о несущественности расхождений, то есть эмпирическое и теоретическое распределения хорошо согласуются между собой.
Рассчитаем теоретические частоты для данного распределения, подставив в формулу для расчета теоретических частот:
|
|
m¢ = N × λy ×e−λ |
= N × p( y) |
|
|
|
|
|
y! |
|
|
|
параметр 0,75 и соответствующие значения числа, |
поступающих заявлений от 0 до 5: |
|
|
|
|
m¢ |
= 365 × |
0,750 ×0,4724 |
= 172,43 |
(0!=1). |
0 |
|
0! |
|
|
|
|
|
|
|
|
|
m1¢ = 365 × |
0,751 ×0,4724 |
=129,32 |
|
|
|
|
1! |
|
|
|
15 Так, уровень значимости α=0,01 означает, что из 100 случаев лишь в одном может быть отвергнута альтернативная гипотеза H1, которую мы проверяем на прочность. Следовательно, чем выше α, тем выше вероятность пропустить ошибку. При α=0,1 из 100 случаев мы можем пропустить ошибку в 10 случаях.











