Лабораторная работа № 2

ИССЛЕДОВАНИЕ

ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА

МЕТОДОМ НАЛОЖЕНИЯ

Цель работы: изучить схемы замещения источников электрической энергии; научиться методом наложения определять токи в ветвях резистивных электрических цепей, содержащих источники напряжения и тока.

2.1. Основные теоретические сведения

Нахождение токов в ветвях электрической цепи, напряжений на элементах цепи производится на основании законов Ома и Кирхгофа. Проверка правильности найденных величин производится частично с использованием законов Кирхгофа, а полная – путем проверки выполнения баланса мощностей.

Для различных схем, с учетом специфики их топологии, разработаны различные методы нахождения токов в электрических цепях:

• метод эквивалентных преобразований;

• метод наложения;

• метод уравнений Кирхгофа;

• метод контурных токов;

• метод узловых потенциалов (частный случай – метод двух узлов);

• метод эквивалентного источника тока;

• метод эквивалентного источника ЭДС.

Рассмотрим особенности нахождения токов в цепях методом наложения.

Для линейных цепей любой ток или напряжение на участке цепи могут быть определены суммой составляющих, рассчитанных отдельно от действия каждого источника или групп источников. Такое свойство линейных цепей называется принципом суперпозиций, или принципом наложения.

Рассмотрим схему, приведенную на рис. 2.1. Поскольку в схеме электрической цепи два источника энергии, то ток в каждой ветви будет складываться из двух составляющих (частичных токов), вызванных каждым из источников в отдельности. Следовательно, исходная схема рис. 2.1 может быть разбита на две вспомогательные (частичные) схемы (рис. 2.2, а и рис. 2.2, б), в каждой из которых остается лишь один источник, другой же заменяется эквивалентным сопротивлением (резистором), равным внутреннему сопротивлению источника.

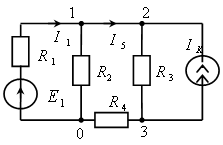
Рис. 2.1. Разветвленная электрическая цепь

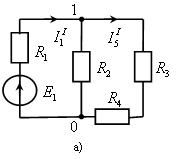
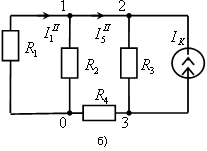
а б

Рис. 2.2. Преобразованные схемы разветвленной электрической цепи

В качестве примера определим метод наложения токов I₁ и I₅:

и

где составляющие ирассчитываются от действия источника ЭДСЕ₁, а составляющие и– от действия источника токаI_k.

Схема для определения составляющих от действия источника ЭДС представлена на рис. 2.2, а. При составлении этой схемы ветвь с источником тока разрывается (если внутреннее сопротивление источника тока не задано, то источник тока считается идеальным и его внутреннее сопротивление берется равным бесконечности).

На рис. 2.2, б изображена схема для определения составляющих токов в ветвях от действия источника тока. При составлении этой схемы источник ЭДС заменен проводником (если внутреннее сопротивление источника ЭДС не задано, то источник ЭДС считается идеальным и его внутреннее сопротивление берется равным нулю).

Составляющие токов в схемах рис. 2.2, а, б можно определить методом эквивалентных преобразований, заменяя параллельно (или последовательно) соединенные элементы на эквивалентные до тех пор, пока в схеме не останется источник энергии и один эквивалентный резистор. Ток в ветви с источником определяется по закону Ома. Далее, разворачивая схему до исходной, вычисляются токи в остальных ветвях:
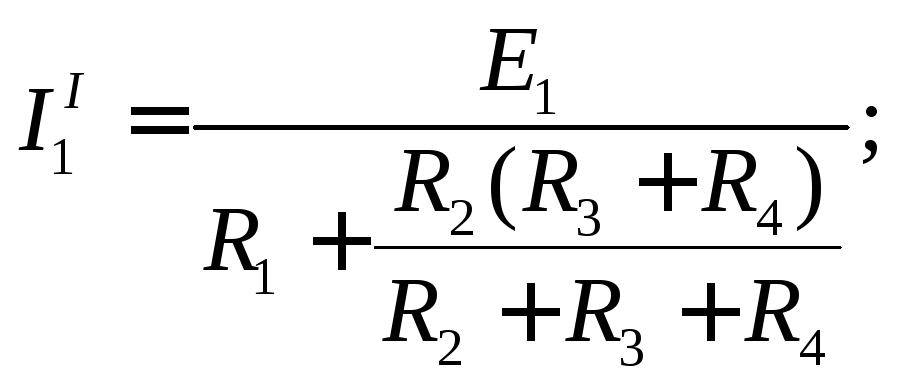