1. Основные теоретические сведения

Нахождение токов в ветвях электрической цепи и нахождение напряжений на элементах цепи производится на основании законов Ома и Кирхгофа.

Для различных схем электрических цепей с учетом специфики их топологии разработаны различные методы нахождения токов.

Рассмотрим методы узловых потенциалов и эквивалентных генераторов.

Ток в любой ветви схемы может быть определен с помощью обобщенного закона Ома по формуле через приложенное к ветви напряжение (разность потенциалов на концах ветви) и параметры элементов ветви (сопротивления резисторов, ЭДС источников). Но чтобы применить обобщенный закон Ома, нужно знать потенциалы узлов. Метод, в котором за неизвестные величины принимают потенциалы узлов, называется методом узловых потенциалов. Причем если один узел заземлить (принять его потенциал равным нулю), то число неизвестных потенциалов сокращается на единицу. Метод целесообразно применять для схем с небольшим числом узлов.

Для схемы с n узлами:

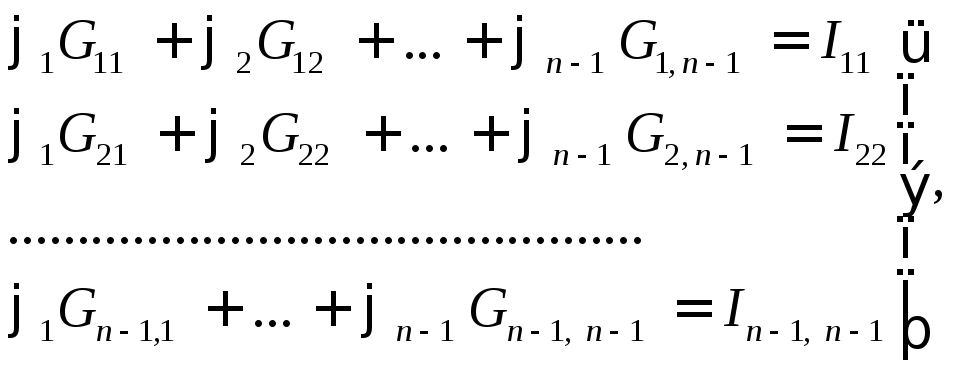(3.1)

где G_kk – сумма проводимостей ветвей, сходящихся в k-том узле;

G_km – сумма проводимостей ветвей, непосредственно соединяющих узлы k и m, взятая со знаком «минус», если между какими-либо двумя узлами нет ветвей, то соответствующая проводимость G_km равна нулю;

I_kk – узловой ток k-того узла (если в узел k втекает ток, то он должен быть добавлен к I_kk со знаком «плюс», а если вытекает – то со знаком «минус»).

Узловой ток I_кк – это расчетная величина, равная алгебраической сумме токов, полученных от деления ЭДС ветвей, подходящих к k-му узлу, на сопротивления данных ветвей (со знаком «плюс» токи тех ветвей, ЭДС которых направлены к данному узлу, иначе «минус»). Узловой ток может быть рассчитан как сумма произведений ЭДС источников, находящихся в ветвях, присоединенных к данному узлу, на проводимости этих ветвей.

После определения узловых потенциалов токи в ветвях определяются по обобщенному закону Ома.

Для примера рассмотрим схему рис. 3.1, содержащую четыре узла и 11 ветвей. Узел № 4 заземлим. Пусть задано:

E₁ = E₆ = 10 В; E₂ = 6 В; E₄ = 20 В; E₅ = 30 В;

E₇ = 14 В; E₈ = 8 В; E₁₀ = 12 В; E₁₁ = 7 В; J₉ = 1,5 А;

R₁ = 1 Ом; R₂ = R₇ =R₈ = R₁₀ = 2 Ом;

R₃ = 5 Ом; R₄ = R₅ = 10 Ом; R₆ = R₉ = 4 Ом.

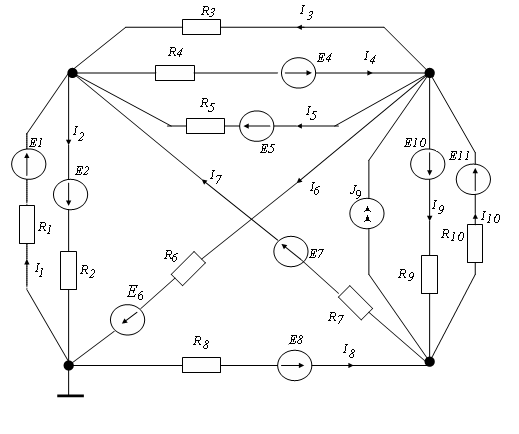
Рис. 3.1. Разветвленная электрическая цепь

Запишем систему уравнений относительно потенциалов узлов:

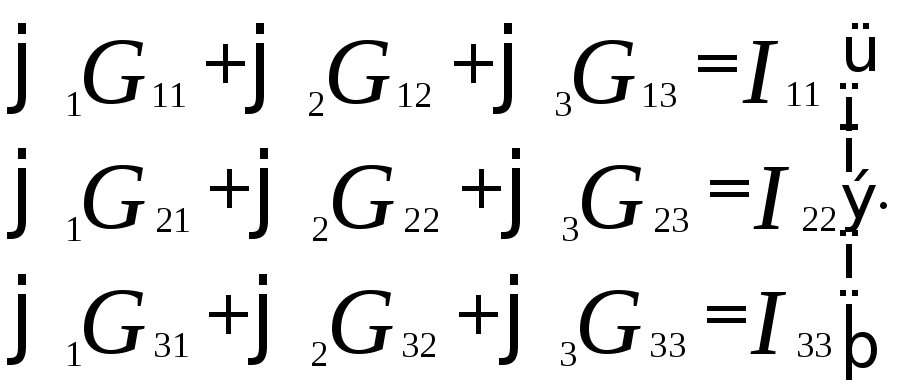
Подсчитаем проводимости:

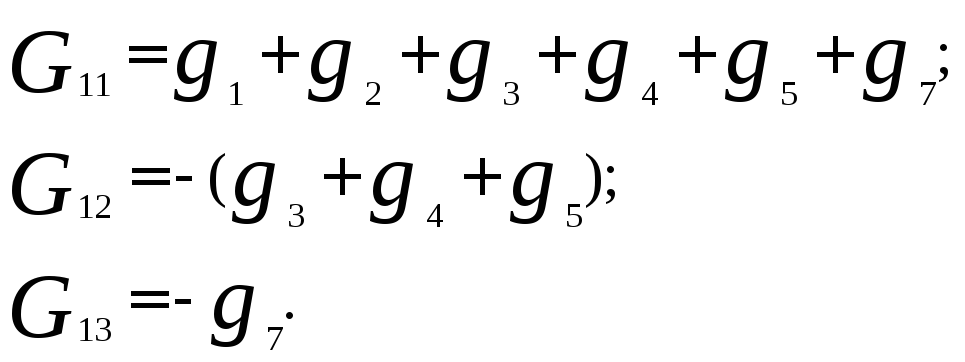
Определим узловые токи:

При вычислении G₂₃, G₃₃, G₂₃ учтем, что проводимость ветви с источником тока J₉ равна нулю.

Подставляем полученные данные в исходную систему уравнений:

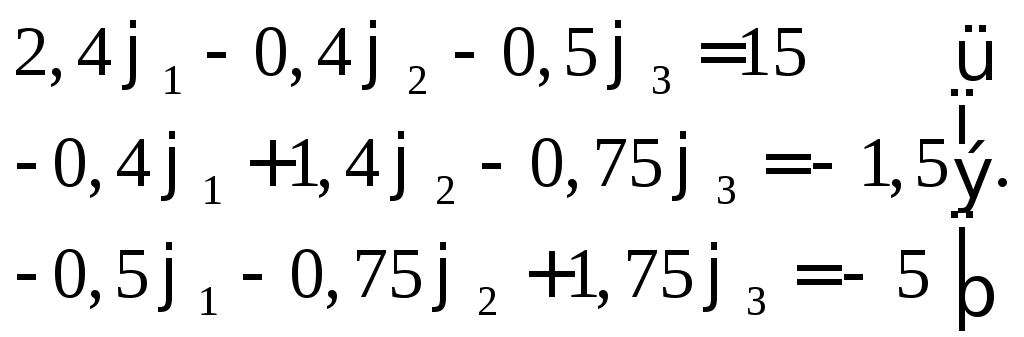
Решим полученную систему с помощью определителей:

3.1.1. Метод двух узлов

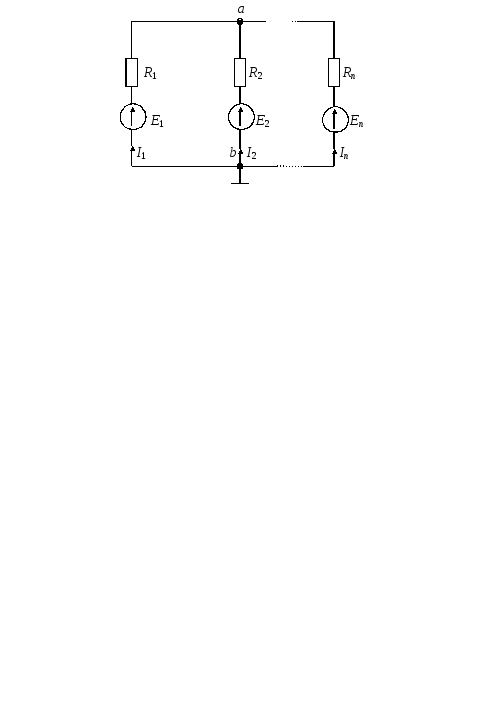
Метод двух узлов используется для расчета схем с двумя узлами и является частным случаем метода узловых потенциалов. Для схемы с n параллельными ветвями для рис. 3.2, согласно формуле (3.1), можно записать:

(3.2)

Рис. 3.2. Схема электрической цепи с двумя узлами

С учетом принятых на рис. 3.2 обозначений последнее соотношение перепишем для частного случая отсутствия источников тока:

(3.3)

После определения U_ab находятся токи в ветвях по уже известной формуле:

I_n = (E_n – U_ab)g_n. (3.4)

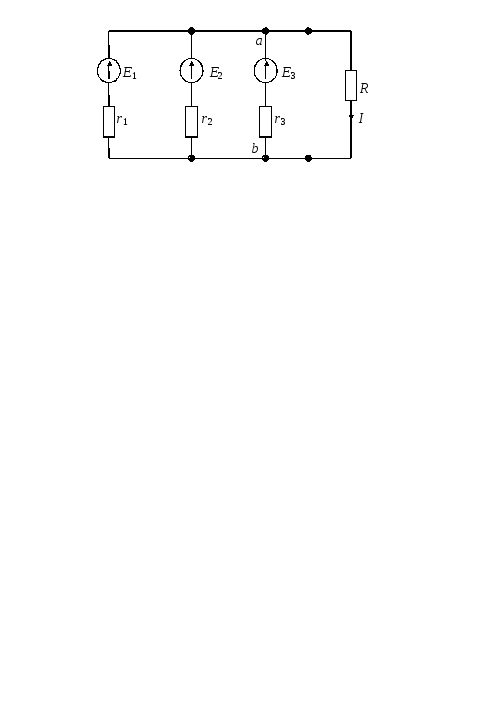
Рассмотрим пример. Три источника ЭДС с напряжениями Е₁ = 48 В; Е₂ = Е₃ = 45 В и внутренними сопротивлениями r₁ = 1,2 Ом, r₂ = 1 Ом, r₃ = 1,5 Ом работают параллельно на общую нагрузку R = 4,2 Ом, как показано на рис. 3.3. Необходимо определить токи в ветвях и напряжение между узлами U_аb.

По формуле (3.3) определяем напряжение U_аb:

Рис. 3.3. Расчетная схема с двумя узлами

По формуле (3.4) (с учетом использования сопротивлений вместо проводимостей) вычисляем искомые токи: