2.4 Решение задачи с использованием процедуры «поиск решения»
Для решения задачи с использованием процедуры «Поиск решения» создается таблица, в которой задаются все известные параметры. Затем вызывается диалоговое окно «Поиск решения», в котором:
Задается ячейка с функцией для оптимизации;
Выбирается, до какого значения будет оптимизирована функция;
Вводятся ячейки, данные в которых можно изменять;
Вводятся ограничения
Найдем максимум
3y1+2y2≤ 1
y2≤ 1
5y1+y2≤ 1
Ф(y) = y1+y2→ max
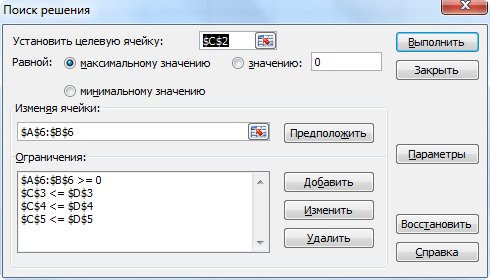
Рисунок 2.4.1 – Окно ввода ограничений
Рисунок 2.4.2 – Результаты работы процедуры «Поиск решений»
ОТЧЕТ «РЕЗУЛЬТАТЫ»
Рисунок 2.4.3 - Отчет «Результаты»
ОТЧЕТ «УСТОЙЧИВОСТЬ»
Рисунок 2.4.4 – Отчет «Устойчивость»
ОТЧЕТ «ПРЕДЕЛЫ»
Рисунок 2.4.5 – Отчет «Пределы»
Найдем минимум
3x1+5x3≥ 1
2x1+x2+x3 ≥ 1
F(x) = x1+x2+x3 → min
Рисунок 2.4.6 – Окно ввода ограничений
Рисунок 2.4.7 – Результаты работы процедуры «Поиск решений»
ОТЧЕТ «РЕЗУЛЬТАТЫ»
Рисунок 2.4.8 - Отчет «Результаты»
ОТЧЕТ «УСТОЙЧИВОСТЬ»
Рисунок 2.4.9 – Отчет «Устойчивость»
ОТЧЕТ «ПРЕДЕЛЫ»
Рисунок 2.4.10 – Отчет «Пределы»
ВЫВОДЫ
В ходе выполнения данного курсового проекта были изучены такие задачи линейного и нелинейного программирования, как метод Франка-Вульфа и решение матричных игр. Для решения задач нелинейного программирования методом Франка-Вульфа была реализована программа. Задача линейного программирования решалась 3 способами, а именно, графически, аналитически и при помощи встроенного средства MicrosoftExcel«Поиск решения».
В играх, где нет седловой точки, решение следует искать в смешанных стратегиях. Для определения оптимальных смешанных стратегий в играх m x n следует использовать симплекс-метод, предварительно переформулировав игровую задачу в задачу линейного программирования.
Таким образом, в данной работе также был изучен симплекс метод, который использовался при нахождении минимума и максимума линейной функции. Симплекс-метод является основным в линейном программировании. Решение задачи начинается с рассмотрений одной из вершин многогранника условий. Если исследуемая вершина не соответствует максимуму (минимуму), то переходят к соседней, увеличивая значение функции цели при решении задачи на максимум и уменьшая при решении задачи на минимум. Таким образом, переход от одной вершины к другой улучшает значение функции цели. Так как число вершин многогранника ограничено, то за конечное число шагов гарантируется нахождение оптимального значения или установление того факта, что задача неразрешима.
Матричные игры вида 2 x n и m x 2 можно решать графически. У таких игр всегда имеется решение, содержащее не более двух активных стратегий для каждого из игроков.
Список литературы
1. Конспект лекций по предмету «Методы и алгоритмы принятия решений» ст. преподаватель Михалевич А.П.
2. Большакова И. В., Кураленко М. В. « Нелинейное программирование. Учебно-методическое пособие к контрольной работе».
3. Васильков Ю.В., Василькова Н.Н. «Компьютерные технологии вычислений в математическом моделировании»
4. Электронный учебник, http://math.mrsu.ru/text/courses/method/metod_franka-vulfa.htm.
5. Электронный ресурс, http://ecosyn.ru/page0175.htmlпо решению матричных игр.