
Цель работы: Изучение алгебраических критериев устойчивости Гурвица и Рауса, частотных критериев устойчивости Михайлова и Найквиста.
Вариант 5

Т1 = 2; Т3 = 1; К1 = К2 = 8
W(p)=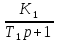 *
* =
=
W(p)= *
* =
=
Wэкв=
W(p)=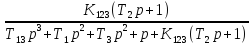
D(p)= =0
=0
a0= =2;
=2;
a1= =3;
=3;
a2=
a3=
Критерий Гурвица:
Δ1= a1>0
Δ2= =a1a2>a3a0
=a1a2>a3a0
3(64K3T2+1)>128K3; 3(64K3T2+1)- 128K3>0; K3(192T2-128)>-3; K3>-3; 192T2-128>-3; T2>0,657
.
Система устойчивая при K3=1, T2=1

Система неустойчивая при K3=1, T2=0,5

Исследование корней характеристического уравнения:
|
D(p)=
|
D(p)=
|
|
-0.2500 + 5.6513i -0.2500 - 5.6513i -1.0000 |
0.1815 + 4.1405i 0.1815 - 4.1405i -1.8630 |
|
Все корни находятся в левой полуплоскости – устойчивая система. |
Корни p1 и p2 находятся в правой полуплоскости – неустойчивая система. |
Критерий Рауса:

 и
и
 :
:
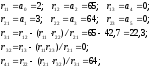
 и
и
 :
:

|
Система устойчива
при:
|
Система неустойчива при: |
|
Результат: элементы первого столбца положительны |
|
Критерий Михайлова:
. =0
=0
3 2=64
2=64
 2=21,3
2=21,3
. =±4,6
=±4,6
.
 (65-
(65- 2)=0
2)=0
 =0, w=±5,7
=0, w=±5,7
______________________________________
. =0
=0
3 2=64
2=64
 2=21,3
2=21,3
. =±4,6
=±4,6
.
 (33-
(33- 2)=0
2)=0
 =0, w=±4,06
=0, w=±4,06
______________________________________
|
Система
устойчивая при:
|
Система неустойчивая при: |
|
D(jw)=
|
D(jw)=
|

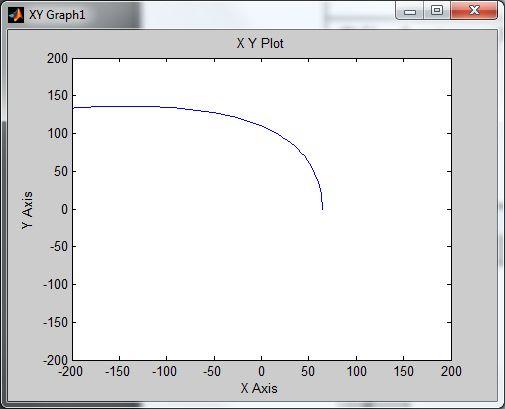
Критерий Найквиста:
|
Замкнутая
исходная система устойчивая при
|
Замкнутая исходная система
неустойчивая при:
|
|
|
|
Передаточная функция замкнутой системы:
W(p)=
Передаточная функция разомкнутой системы:
W(p) =
=
W(p) =
=
T2=1, K=1
a=64p
b=64
c=Re=-3p2
d=Im=p+2p3

T2=0,5, K=1
a=32p
b=64
c=Re=-3p2
d=Im=p+2p3

Вывод: Устойчивость является одним из главных требований, предъявляемых к автоматическим системам. Выбирая любой критерий устойчивости, можно определить устойчивость всей системы до n-го порядка. Причем, алгебраический критерий Гурвица целесообразно применять при n≤4, критерий Рауса – при n=4÷6. Критерий Михайлова применим для исследования сложный многоконтурных систем, когда необходимо выяснить влияние изменение структуры системы и средств ее стабилизации на устойчивость. Если система имеет одноконтурный вид, и отдельные элементы заданы экспериментально, то применяют критерий Найквиста.

 =0
=0 =0
=0 и
и

 и
и


 и
и
 :
: и
и

 =0
=0

 =0
=0

 и
и
 :
: и
и


