8
.pdf
Скачано с http://antigtu.ru
Задача Кузнецов Пределы 1-8
Условие задачи
Доказать, что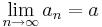 
(указать 
).
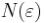Решение
По определению предела:
:
Проведем преобразования:
(*)
Очевидно, что предел существует и равен 2.
Из (*) легко посчитать 
:
Задача Кузнецов Пределы 2-8
У этой задачи может быть и другое условие (возможно из-за разных изданий или ошибки).
Условие задачи
Вычислить предел числовой последовательности:
Решение
Задача Кузнецов Пределы 2-8(2)
Условие задачи
Вычислить предел числовой последовательности:
Решение
Задача Кузнецов Пределы 3-8
Условие задачи
Вычислить предел числовой последовательности:
Решение
Задача Кузнецов Пределы 4-8
Условие задачи
Вычислить предел числовой последовательности:
Решение
Задача Кузнецов Пределы 5-8
Условие задачи
Вычислить предел числовой последовательности:
Решение
Задача Кузнецов Пределы 6-8
Условие задачи
Вычислить предел числовой последовательности:
Решение
={Используем второй замечательный предел}=
Задача Кузнецов Пределы 7-8
Условие задачи
Доказать, что (найти 
):
Решение |
|
|
|
|
Согласно определению предела функции по Коши: |
|
|
||
если дана функция |
и |
— предельная точка множества |
Число |
|
называется пределом функции |
при |
стремящемся к |
, если |
|
Следовательно, необходимо доказать, что при произвольном 
найдется такое 
, для которого будет выполняться неравенство:
, если выполнено 
При 
:
или
Таким образом, при произвольном 
неравенство
будет выполняться, если будет выполняться неравенство
, где 
.
Следовательно, при 
предел функции существует и равен 7, а 
.
Задача Кузнецов Пределы 8-8
Условие задачи
Доказать, что функция 
непрерывна в точке 
(найти 
):
Решение
По определению функция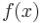 
непрерывна в точке 
, если 
.
Покажем, что при любом 
найдется такое 
, что 
при
.
Следовательно:
Т.е. неравенство 
выполняется при 
. Значит,
функция непрерывна в точке 
и 
.
Задача Кузнецов Пределы 9-8
Условие задачи
Вычислить предел функции:
Решение
Задача Кузнецов Пределы 10-8
Условие задачи
Вычислить предел функции:
Решение
Задача Кузнецов Пределы 11-8
Условие задачи
Вычислить предел функции:
Решение
Воспользуемся заменой эквивалентных бесконечно малых:
, при 
Получаем:
Задача Кузнецов Пределы 12-8
Условие задачи
Вычислить предел функции:
Решение
Замена:
Получаем:
Воспользуемся заменой эквивалентных бесконечно малых:
, при 
Получаем:
Задача Кузнецов Пределы 13-8
Условие задачи
Вычислить предел функции:
Решение
Замена:
Получаем:
Воспользуемся заменой эквивалентных бесконечно малых:
, при 
Получаем:
Воспользуемся заменой эквивалентных бесконечно малых:
, при 
Получаем:
Задача Кузнецов Пределы 14-8
Условие задачи
Вычислить предел функции:
Решение
Воспользуемся заменой эквивалентных бесконечно малых:
, при 
, при 
, при 
, при 
Получаем:
Задача Кузнецов Пределы 15-8
Условие задачи
Вычислить предел функции:
Решение
Воспользуемся заменой эквивалентных бесконечно малых: