МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Нижегородский государственный университет им. Н.И. Лобачевского»

Механико-математический факультет

Кафедра теоретической механики

КУРСОВАЯ РАБОТА

Динамика вращения ротора с демпфером.

Исполнитель:

Студент 646 группы

Юкалов А.В.

Научный руководитель:

Доцент кафедры

теоретической механики

Ляхов А.Ф.

Нижний Новгород

2012

Оглавление

1. Введение.............................................................................................................................3

2. Постановка задачи…………………………………………...……...…………………...3

3. Моделирование движения ротора на горизонтальной плоскости ……………………3

4. Заключение……………...………………………………………………………..............6

5. Список литературы ...........................................................................................................6

Введение

При вращении упругого ротора с угловой скоростью, превышающей первую критическую скорость, внутреннее трение в материале ротора может при определенном сочетании параметров внутреннего и внешнего демпфирования приводить к неустойчивости вращения ротора. Этот факт хорошо известен и описан в научной и учебной литературе. Тем не менее, для каждой конкретной конструкции ротора целесообразно изучать этот вопрос на основе соответствующих математических моделей. В настоящем отчете анализируется математическая модель ротор – демпфер.

Постановка задачи

• Вывести уравнения движения ротора с демпфером, найти уравнение зависимости для момента

• Написать для данной системы программу позволяющую рассчитать траекторию движения и построить её график

• С помощью программы исследовать динамику вращения ротора при различных параметрах системы.

• Найти критическую скорость вращения

Моделирование движения ротора на горизонтальной плоскости

Представим вертикальный невесомый вал круглого сечения сосредоточенным диском, центр которого перемещается в плоскости, параллельной плоскости Oxy . Вал вращается равномерно с угловой скоростью ω.

Рис. 1. Модель взаимодействия ротора и ограничивающего демпфера

m1 − масса ротора, m2 − масса демпфер, I − момент инерции ротора, k0 − коэффициент упругости самого ротора, k1 – упругость роторной иглы, k2 − упругость основного демпфера

Рассмотрим перемещения центра масс ротора в плоскости демпфера ограничителя.

центр масс ротора С смещён от геометрического центра ротора O1 , (рис. 2).

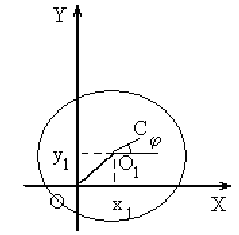
Рис. 2. Связь между положением геометрического центра и центра масс ротора

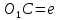− эксцентриситет. В плоскости диска введём неподвижную систему координат

OXY. Координаты центра масс:

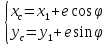
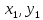− координаты геометрического центра ротора. Эти координаты определяют

смещение ротора как целого.

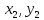− координаты смещения демпфера.

Запишем функцию Лагранжа в неподвижной системе координат.

Кинетическая энергия ротора:

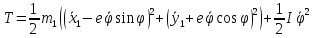
Потенциальная энергия магнитного подвеса ротора:

Потенциальная энергия иглы ротора:

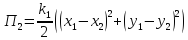
Функция Лагранжа демпфера:

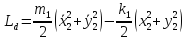
Полная функция Лагранжа имеет вид:

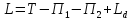
Уравнения движения ротора:

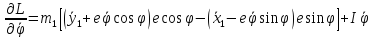
Или

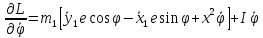
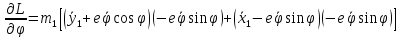
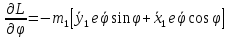
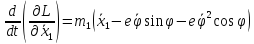
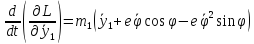
Уравнения движения:

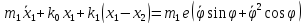
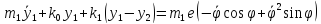
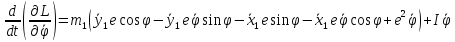
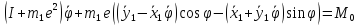
Где 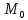− внешний момент, приложенный к ротору.

Пусть ротор вращается с постоянной скоростью, то есть

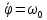
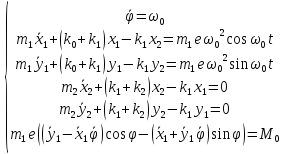
Введем обозначения:

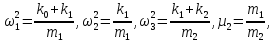
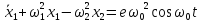
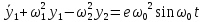
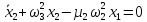
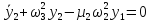
Введём, как это принято в теории динамики ротора, внешнее и внутреннее

демпфирование:

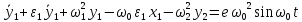
Где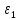− коэффициент внутреннего демпфирования ротора,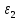 − коэффициент

демпфирования закрепления.

Заключение.

Написана программа в среде Matlab, позволяющая проводить непосредственное вычисление динамики ротора и демпфера при заданных параметрах.

Рассмотрено вращение ротора при различных параметрах.

Используемая литература

1. Болотин В.В. Неконсервативные задачи теории упругой устойчивости. М: ФИЗМАТГИЗ. 1961, 339 с.

2. Бабицкий В.И. Теория виброударных систем М.: Наука 1978, 352с.