
определитель
.rtf3. Определители
3.1. Определители 2-го и 3-го порядков
Каждое число считают, по определению, определителем (детерминантом) 1-го порядка.
Определение 1. Дана квадратная матрица 2-го порядка
А= .
.
Определителем 2-го порядка называется число, вычисленное из элементов этой матрицы по следующему правилу:
D
= det(A) =
 =
a1b2
– a2
b1.
=
a1b2
– a2
b1.
Определение 2. Дана квадратная матрица 3-го порядка
A
=
 .
.
Определителем 3-го порядка называется число, вычисленное из элементов этой матрицы по следующему правилу:
D
= det(A) =
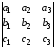 = a1
= a1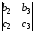 – a2
– a2 + a3
+ a3 .
.
Таким образом, определитель 3-го порядка вычисляется через определители 2-го порядка.
3.2. Определитель n-го порядка
Определение 3. Дана квадратная матрица n-го порядка
А
=
 .
.
Определителем n-го порядка называется число, вычисленное из элементов этой матрицы по следующему правилу:
D
= det(A) =
 =
=
= a11D1 – a12 D2 + a13 D3 – … + (–1)n+1 a1n Dn,
где Di (i = 1, 2, … , n) – определитель (n–1)-го порядка, полученный из D вычеркиванием 1-й строки и i-го столбца.
Например, определитель 4-го порядка вычисляется через определители 3-го порядка
D
=
 =
=
= a11D1 – a12 D2 + a13 D3 – a14 D4 =
=
a11 –
a12
–
a12 +
a13
+
a13 –
a14
–
a14 .
.
Определитель 5-го порядка вычисляется через определители 4-го порядка, которые, в свою очередь, уже вычислены через определители 3-го порядка. И т.д. вплоть до определителя произвольного порядка.
3.3. Свойства и преобразования определителей
1. При транспонировании матрицы определитель не изменяется.
2. Если квадратная матрица содержит две одинаковые строки (столбца), то ее определитель равен нулю.
3. Если
все элементы какой-либо строки (столбца)
матрицы умножить на число
![]() ,
то ее определитель умножится на это
число
,
то ее определитель умножится на это
число
![]() .
.
4. Если элементы какой-либо строки (столбца) матрицы представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующий определителей. Например,
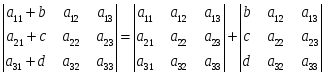 .
.
5. Определитель не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), предварительно умноженные на одно и то же число.
 .
.
6. Если какая-либо строка (столбец) матрицы состоит из одних нулей, то ее определитель равен нулю.
7. Сумма произведений элементов какой-либо строки (столбца) на алгебраические дополнения соответствующих элементов другой строки (столбца) этой матрицы равна нулю.
8. Если матрица А имеет треугольный вид
А
=
 ,
,
то ее определитель равен
|А|
= = a11
a22
a33
…
ann.
= a11
a22
a33
…
ann.
Определение
4.
Пусть
дана квадратная матрица А n-го
порядка. Минором
![]() элемента
элемента
![]() матрицы n-го
порядка называется определитель матрицы
(n–1)-го
порядка, полученной из матрицы А
вычеркиванием i-ой
строки и j-го
столбца.
матрицы n-го
порядка называется определитель матрицы
(n–1)-го
порядка, полученной из матрицы А
вычеркиванием i-ой
строки и j-го
столбца.
Например,
минором элемента
![]() матрицы А
третьего порядка будет:
матрицы А
третьего порядка будет:
 .
.
Каждая
матрица n-го
порядка имеет
![]() миноров (n–1)-го
порядка.
миноров (n–1)-го
порядка.
Определение
5.
Алгебраическим
дополнением
![]() элемента
элемента
![]() матрицы
n-го
порядка называется его минор, взятый
со знаком
матрицы
n-го
порядка называется его минор, взятый
со знаком
![]() :
:
![]() ,
,
т.е. алгебраическое дополнение совпадает с минором, когда сумма номеров строки и столбца (i+j) – четное число, и отличается от минора знаком, когда (i+j) – нечетное число.
Например,
![]() ,
,
![]()
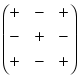
Для
определителей третьего порядка знаки
![]() ,
с которыми миноры входят в алгебраические
дополнения, таковы:
,
с которыми миноры входят в алгебраические
дополнения, таковы:
Теорема Лапласа (теорема о разложении определителя). Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
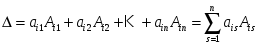
(разложение по элементам i-й строки; i =1, 2,…, n );
![]()
(разложение по элементам j-го столбца; j=1,2,…,n );
Наиболее эффективный способ вычисления определителя состоит в сочетании теоремы о разложении и свойств определителя: целесообразно так преобразовать исходную матрицу, чтобы преобразованная матрица имела строку (или столбец), содержащую как можно больше нулей, а потом найти определитель разложением по этой строке (столбцу).
