
Шпаргалки (фу!) / МП 2 курс / шпора
.pdf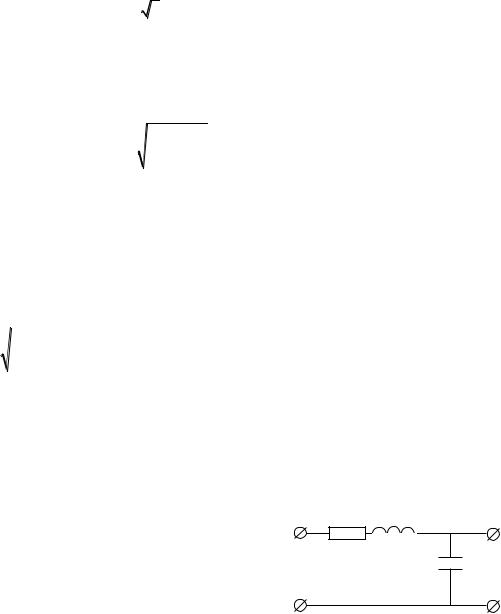
48. Задача на А – параметры.
Зная результаты измерений, вычислим А – параметры и затем построим эквивалентную схему замещения.
Дано:
В результате опытов были получены следующие данные:
U1x 100 В. |
|
|
|
U1k |
70.7 В. |
|
|
U2k |
56.6 В. |
||||||||||
I1x 20 А. |
|
|
|
I1k 10 А. |
|
|
|
|
|
|
I2k 8 А. |
||||||||
P |
2 кВт. |
|
|
|
P |
0.5 кВт. |
|
|
P |
320 Вт. |
|||||||||
1x |
|
|
|
|
|
|
1k |
|
|
|
|
|
|
|
|
|
|
2k |
|
|
|
|
|
1k 0 |
|
|
|
|
2k 0 . |
|
|
|
|||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итак, определим Z1x : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
U1x |
5 |
|
|
|
|
|
0 |
|
|||||||
|
|
|
|
||||||||||||||||
|
|
|
1x |
|
|
I1x |
|
|
|
|
|
|
|
1x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Определим Z1k : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U1k |
7.07 5 |
|
|
|
|
|
|
|
45 , |
|||||||
|
Z |
2 |
|
|
|||||||||||||||
|
|
|
|||||||||||||||||
|
1k |
|
I1k |
|
|
|
|
|
|
|
|
|
|
|
1k |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
Z1k |
|
5 5 j |
|
|
|
|
|
|
|
|
||
Проделав аналогичные вычисления, получим, что |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
Z2k |
5 5 j . |
|
|
|
|
|
||||||
Определяем À параметры: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
Z1x |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Z2 x Z2k |
|
|
|
|
|
|||||
а Z2 x нам взять неоткуда. Воспользуемся такой формулой:
|
|
|
|
|
|
|
|
|
|
|
Z1x |
|
Z1k |
|
, |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Z2 x |
|
|
Z2k |
|
|
|
|
|
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
Z |
Z2k |
5 |
5 5 j |
|
5 |
1 j |
5 j . |
|||||||
|
|
|
|
|
5 5 j |
|
|||||||||||||
|
|
|
|
2 x |
1x Z |
|
|
|
|
|
1 j |
||||||||
|
|
|
|
|
|
|
|
1k |
|
|
|
|
|
|
|
|
|
|
|
Теперь можем определить наши À параметры: |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
5 |
|
|
|
j |
|
|
|
|
|
|
|
|
B j 5 5 j 5 5 j |
|||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
5 j 5 5 j |
|
|
|
|
|
|
|
|
|||||||||||
C |
j |
0.2 j |
|
|
|
|
|
|
|
|
|
|
D 5 j 0.2 j 1. |
||||||
5 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теперь построим Т – образную схему замещения:
Z |
A 1 |
|
|
j 1 |
5 5 j . |
|
|
||||
1 |
C |
|
0.2 j |
||
|
|
||||
Z |
|
|
D 1 |
|
0 |
Z |
|
|
1 |
|
1 |
5 j . |
|
2 |
C |
3 |
C |
0.2 j |
|||||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||
Таким образом, эквивалентная схема замещения будет иметь вид, изображенный на рисунке.
61
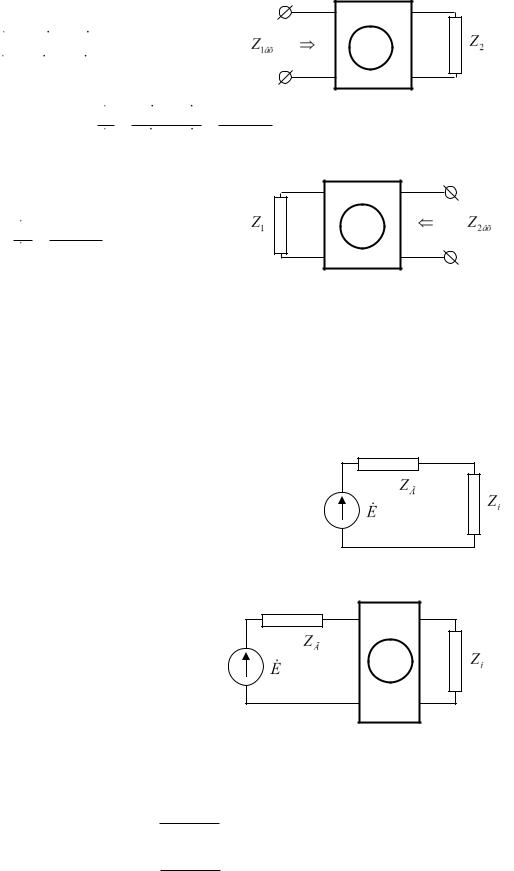
49. Характеристические параметры четырехполюсников. |
|||||||||||||||||
Здесь мы как раз обращаемся к той самой 6-й системе, описывающей четырехполюсники: |
|||||||||||||||||
системе в характеристических параметрах. |
|
|
|
|
|||||||||||||
Пассивный четырехполюсник, изображенный справа, |
|
|
|
||||||||||||||
описывается следующей системой: |
|
|
|
|
|
|
|
||||||||||
|
|
|
U |
AU |
|
BI |
|
|
|
|
|
|
П |
|
|||
|
|
|
|
1 |
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
I1 CU2 DI2 |
|
|
|
|
|
|
|
|||||||
Посмотрим на Z1âõ : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
Z |
U1 AU2 BI2 AZ2 B . |
|
|
||||||
|
|
|
|
|
|
|
|
1âõ |
|
I1 |
CU2 DI2 |
CZ2 D |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Возьмем тот же самый четырехполюсник, поставим на вход сопротивление Z1 |
и |
||||||||||||||||
посмотрим на входное сопротивление Z2âõ |
со |
|
|
|
|
||||||||||||
стороны вторичных зажимов: |
|
|
|
|
|
|
|
|
|
||||||||
|
|
Z |
2âõ |
U2 DZ1 B - |
|
|
|
|
|
П |
|
||||||
|
|
|
|
I2 |
CZ1 A |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
с учетом того, что токи будут протекать в обратном |
|
|
|
|
|||||||||||||
направлении. Т.е. получили очень любопытную вещь: |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
Z1âõ f Z2 , A, B,C, D |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
Z2âõ f Z1, A, B,C, D |
|
|
|
||||
Т.е. наш четырехполюсник является преобразователем сопротивления. Т.е. |
|||||||||||||||||
сопротивление |
нагрузки |
|
|
Z2 |
|
источник, подключаемый ко |
входным |
зажимам, |
|||||||||
воспринимает как совершенно другое, преобразованное сопротивление. Аналогично для |
|||||||||||||||||
нагрузки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим |
|
цепь, |
|
изображенную |
справа; |
здесь |
ZÃ |
|
|
||||||||
сопротивление генератора, |
Zí сопротивление нагрузки. Одна из |
|
|
||||||||||||||
задач радиоэлектроники – передача максимальной мощности от |
|
|
|||||||||||||||
источника в нагрузку. Т.е. задача в том, чтобы обеспечить |
|
|
|||||||||||||||
согласованный режим работы генератора и нагрузки (их |
|
|
|||||||||||||||
сопротивления должны отличаться только знаком мнимой части). |
|
|
|||||||||||||||
Итак, пусть в общем случае сопротивления |
|
|
|
|
|||||||||||||
генератора и нагрузки несогласованны. Тогда мы |
|
|
|
|
|||||||||||||
включаем для их согласования пассивный |
|
|
|
|
|||||||||||||
четырехполюсник (см. рисунок), который как раз и |
|
|
П |
||||||||||||||
обеспечит режим согласования. При согласовании |
|
|
|
|
|||||||||||||
генератора с нагрузкой четырехполюсник содержит |
|
|
|
|
|||||||||||||
только реактивные элементы (если добавить |
|
|
|
|
|||||||||||||
активный элемент, на нем будет только |
|
|
|
|
|||||||||||||
рассеиваться мощность). Наши характеристические параметры как раз и служат для |
|||||||||||||||||
обеспечения согласованного режима. |
|
|
|
|
|
|
|
||||||||||
Выберем Z1 |
и Z2 |
таким образом, чтобы два уравнения выполнялись одновременно: |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
AZ2c B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z1c |
CZ2c D |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
DZ2c B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
2c |
|
CZ1c A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
62 |
|
|
|
|
|
|

Решив эту систему уравнений, найдем:
Z1c AB CD
Введем следующие обозначения: ch g 
 AD Вспомним:
AD Вспомним:
ch x |
ex e x |
sh x |
ex e x |
|
2 |
2 |
|||
|
|
Тогда:
Z2c DB CA
sh g 
 BC
BC
ch2 x sh2 x 1 |
AD BC 1. |
|
|
|
|
Z1c |
|
|
A |
|
|
|
Z |
Z |
|
|
|
|
|
B |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2c |
|
|
|
|
|
|||||||||||||
|
|
|
|
Z2c |
|
|
|
D |
|
|
|
|
1c |
|
|
|
|
C |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Вспоминаем об A параметрах: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
U AU |
|
BI |
|
|
|
|
Z1c |
|
ch g U |
|
|
|
|
|
|
|
|
|
|
|
|
sh g I |
|
1 |
|||||||||
2 |
2 |
|
|
|
2 |
|
Z |
|
|
|
Z |
2c |
|
2 |
|||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
Z2c |
|
|
|
|
1c |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
I CU |
|
DI |
|
|
|
|
1 |
|
|
sh g U |
|
|
|
|
|
Z2c |
ch g I |
|
|
2 |
|||||||||||||
2 |
2 |
|
|
|
|
|
|
|
2 |
|
|
2 |
|||||||||||||||||||||
1 |
|
|
|
|
|
|
|
Z1c Z2c |
|
|
|
|
|
|
|
Z1c |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
В общем случае g комплексная величина: |
g a jb |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
a коэффициент затухания или коэффициент амплитуды, |
|
b коэффициент фазы. |
|||||||||||||||||||||||||||||||
1 |
|
Z1c |
|
|
Z2c |
|
|||
|
|
|
|
|
2 |
|
Z2c |
|
|
|
Z1c |
|
||
|
|
|
|
|
ch g U |
2 |
Z |
||
|
|
|
|
|
|
1 |
sh g |
U2 |
|
|
|
|||
|
||||
Z2c |
|
|
|
|
2c sh g I |
|
3 |
2 |
ch g I2 4
|
|
|
|
|
Z2c Z2 |
|
|
U |
2 |
I2 |
||||
Согласованный режим работы означает, что |
|
|
||||||||||||
|
|
|||||||||||||
|
|
|
|
|
Z2 I2 U2 |
|
|
|
|
|
|
Z2 |
|
|
3 |
Z1c |
|
ch g sh g U2 |
|
Z1c |
|
egU2 |
|
|
|
||||
|
|
|
|
|
|
|
||||||||
|
|
Z2c |
|
Z2c |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||
4 |
|
Z2c |
sh g ch g I2 |
Z2c |
eg I2 , |
|
|
|
||||||
|
|
|
|
|
|
|||||||||
|
|
|
Z1c |
|
Z1c |
|
|
|
||||||
здесь g a jb . В согласованном режиме отношение амплитуд будет определяться так:
|
|
U1 |
|
|
|
|
Z1c |
|
ea |
|
|
|
|
I1 |
|
|
|
|
|
|
|
|
Z2c |
|
ea |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
U2 |
|
|
|
|
Z2c |
|
|
|
|
|
|
|
I2 |
|
|
|
|
|
|
|
|
|
Z1c |
|
|||||
Коэффициент a показывает затухание. Чтобы окончательно прояснить физический |
||||||||||||||||||||||||||||||
смысл, рассмотрим симметричный четырехполюсник, у которого Z1c Z2c . |
||||||||||||||||||||||||||||||
Тогда для симметричного четырехполюсника получаем: |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U1 |
ea |
|||||||||
|
|
U |
egU |
|
|
|
|
|
U |
2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
I1 eg I2 |
|
|
|
|
|
|
|
|
I1 |
|
e |
a |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I2 |
|
|
|
||||||
Теперь ясно, |
почему a коэффициент амплитуды. Единицы измерения коэффициента |
|||||||||||||||||||||||||||||
затухания: Í ï |
- непер. 1 Нп соответствует затуханию амплитуды в е раз. |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
a |
|
|
e |
U2 |
|
e |
|
I2 |
. |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
Í ï |
|
|
n U |
1 |
|
|
n |
|
I |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
63

В радиотехнике принята еще одна единица затухания – Бэл – это отношение кажущихся мощностей:
|
S |
U |
1 |
|
I |
|
U |
1 |
2 |
|
U |
1 |
|
||
aÁ lg |
1 |
lg |
|
|
1 |
|
для сим м етричн ы х четы рехп о лю сн ико в lg |
|
|
2lg |
|
. |
|||
|
|
|
|
|
|
|
|
|
|||||||
|
S2 |
U2 |
|
I2 |
U2 |
|
U2 |
||||||||
Один Бэл соответствует затуханию амплитуды в 10 раз, два Бэла – в сто раз! Единица измерения децибел - в 10 раз меньше:
aäÁ 20 lg U1 20 lg I1 .
U2 I2
1 Í ï 8,686 äÁ .
1 äÁ 0,115 Í ï .
1 äÁ соответствует затуханию амплитуды в 1,12 раз.
64
50. Последовательное соединение четырехполюсников.
Задача: Даны два элементарных четырехполюсника, соединенных определенным образом. Нужно определить любые параметры результирующего четырехполюсника, который получился, в данном случае, в результате последовательного соединения. Мы имеем дело
с |
пассивными |
линейными |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
четырехполюсниками. |
|
|
На |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
прошлой |
лекции |
мы |
записали |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
признаки соединения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
U1 U1 U1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
U |
|
U |
U |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
2 |
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1 I1 I1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
I |
2 |
I |
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Параметры |
|
|
|
|
|
|
первого |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
четырехполюсника: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
U Z |
I |
Z I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
11 |
1 |
12 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
Z |
I Z |
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
2 |
|
|
21 1 |
22 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично, параметры второго четырехполюсника: |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
U Z I Z |
I |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
11 |
1 |
|
|
12 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
Z |
I Z |
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
21 |
1 |
|
22 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
Суммируем почленно системы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
U1 U1 |
U1 |
|
Z11 |
Z11 |
I1 Z12 Z12 |
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
U2 U2 |
U2 |
|
Z21 |
Z22 I1 |
|
Z21 |
Z22 |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
Z |
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
11 |
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
21 |
Z |
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
Z |
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
12 |
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
22 |
|
Z |
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Или в матричном виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
U |
U |
|
U |
|
|
|
Z |
|
I |
|
|
|
Z |
|
|
I |
|
|
Z |
|
|
|
Z |
|
I |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Z Z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
При последовательном соединении складываются матрицы Z параметров исходных четырехполюсников.
65
51. Параллельное соединение четырехполюсников.
Записываем признаки соединения:
U1 U1 U1 |
||||||
U |
|
|
U |
U |
|
|
|
|
2 |
2 |
|
2 |
|
|
|
I1 I1 I1 |
|
|||
|
I |
2 |
I |
I |
|
|
|
|
|
2 |
2 |
|
|
Результирующий ток определяется как сумма токов:
I |
I I |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
Y |
U |
|
U |
|
|||||
Y Y U
Y Y Y
При параллельном соединении складываются матрицы Y параметров исходных четырехполюсников.
66
52. Каскадное соединение четырехполюсников.
Каждое соединение описывается своими параметрами. Признаки соединения:
|
|
|
|
|
|
|
I1 I1 |
|
|
|
U1 U1 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
I |
|
I |
|
|
|
U |
|
U |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
I |
2 |
|
|
|
U |
|
U |
2 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||
U |
|
U |
A |
U |
A |
U |
A A |
U |
A |
A |
U |
|
|
||||||||||||||||
|
1 |
|
|
1 |
|
|
|
|
2 |
|
|
1 |
|
|
|
2 |
|
|
|
|
2 |
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
I |
|
|
I |
|
|
|
I |
|
|
|
|
|
I |
|
|
|
|
I |
|
|
|
|
|
I |
2 |
|
||
1 |
1 |
|
|
|
2 |
|
|
1 |
|
|
|
2 |
|
|
|
||||||||||||||
При каскадном соединении матрица A параметров |
равна произведению матриц A |
||||||||||||||||||||||||||||
параметров исходных четырехполюсников.
67
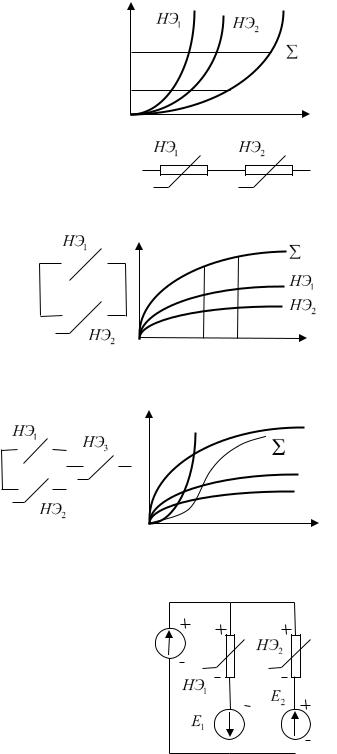
54, Методы расчета нелинейных элементов.
Существуют графические, графо-аналитические и аналитические методы расчета.
1. Графические методы расчета. |
I |
|
|
Пусть даны два нелинейных элемента НЭ1 и НЭ2 |
|
(см. рис.). Для графического метода расчета оба эти элемента должны быть заданы своими графическими характеристиками.
Последовательное соединение:
Вслучае последовательного соединения ток через нелинейные элементы одинаков, результирующую характеристику строим путем
сложения значений напряжений при одинаковых
значениях тока:
U I U1 I U2 I
|
Параллельное соединение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|||||
|
В |
случае параллельного |
соединения |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
напряжение |
|
на |
|
нелинейных |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
элементах |
|
будет |
одинаково, |
|
|
|
|
|
|
||||||||||
|
следовательно, |
|
результирующую |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
характеристику |
|
строим |
путем |
|
|
|
|
|
|
||||||||||
|
сложения |
значений |
тока |
при |
|
|
|
|
|
|
||||||||||
|
одинаковых значениях напряжения: |
|
|
|
|
|
|
|||||||||||||
|
|
|
I U I1 U I2 U |
|
|
|
|
|
|
|||||||||||
|
Смешанное соединение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
||||
|
В |
данном |
случае |
(см. |
рис.) |
3 |
||||||||||||||
|
характеристики |
первого |
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
второго |
элемента |
будут |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||||||
|
складываться при |
одинаковых |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
значениях напряжения, а затем |
|
|
|
|
|
|
|||||||||||||
|
результирующий для 1 и 2 |
|
|
|
|
|
|
|||||||||||||
|
элементов график будет складываться с характеристикой 3 элемента при |
|||||||||||||||||||
|
одинаковых значениях токов. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
U
U
1+2
2
1
U
Все проделанные рассуждения проводились для случая, когда в рассматриваемом участке цепи нет источников. В том случае, если источники в цепи присутствуют, нужно U учитывать сдвиг, который эти источники обеспечивают.
Для случая, изображенного на рисунке, имеем:
E1 UНЭ2 E2 . Характеристика «средней» ветви будет смещена влево на
величину E1 , характеристика «правой» ветви – вправо на 

 величину E2 . Перпендикуляр к оси напряжений в точке U соответствует источнику, поддерживающему постоянное напряжение на зажимах оставшейся системы. Поэтому зафиксировав значения токов I1 и I2 , при которых на системе
величину E2 . Перпендикуляр к оси напряжений в точке U соответствует источнику, поддерживающему постоянное напряжение на зажимах оставшейся системы. Поэтому зафиксировав значения токов I1 и I2 , при которых на системе
«нелинейный элемент – источник» достигается напряжение U , и сложив эти значения, можно получить результирующий ток:
68
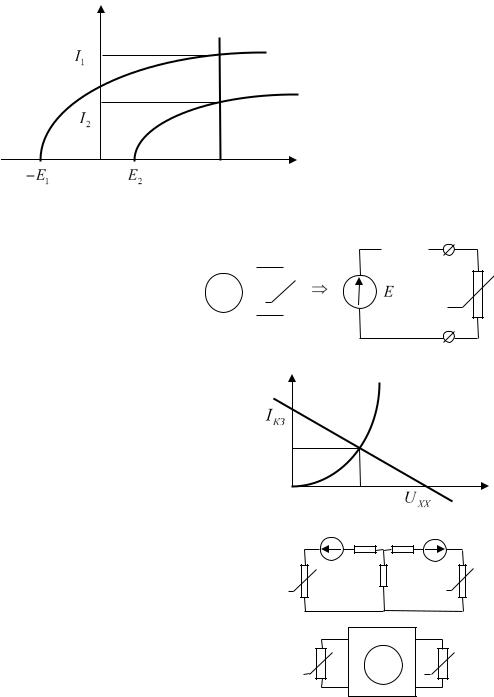
I
|
|
U |
|||||||
Рассмотрим |
еще один случай: пусть |
|
|
|
|
|
|
|
R |
имеется сложная схема, содержащая один |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
нелинейный элемент. Например, пусть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
дан активный двухполюсник (см. рис.), |
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
нагруженный на нелинейный элемент и |
|
|
|
|
|
|
|
||
наша задача – определить ток и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
напряжение на нелинейном элементе. По |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
теореме об |
эквивалентном генераторе, |
|
|
|
|
|
|
|
|
приводим исходную схему к виду, изображенному |
I |
|||||
на рисунке ниже. После чего поступаем |
||||||
|
||||||
следующим образом. Нагрузочная характеристика |
|
|||||
эквивалентного генератора характеризуется двумя |
|
|||||
особыми точками: IКЗ |
и U XX . |
Тогда построив на |
I |
|||
|
|
|
|
|
||
том же |
графике ВАХ нелинейного элемента |
и |
U |
|||
определив точку пересечения двух графиков, |
||||||
|
||||||
получим |
значения |
тока и |
напряжения |
на |
U |
|
нелинейном элементе.
Пусть теперь в рассматриваемой схеме два нелинейных элемента, расположенных так, как это показано на рисунке. В этом случае определяем параметры Т- образного четырехполюсника, пользуемся теоремой об
активном четырехполюснике и строим нужные графики.
А
69
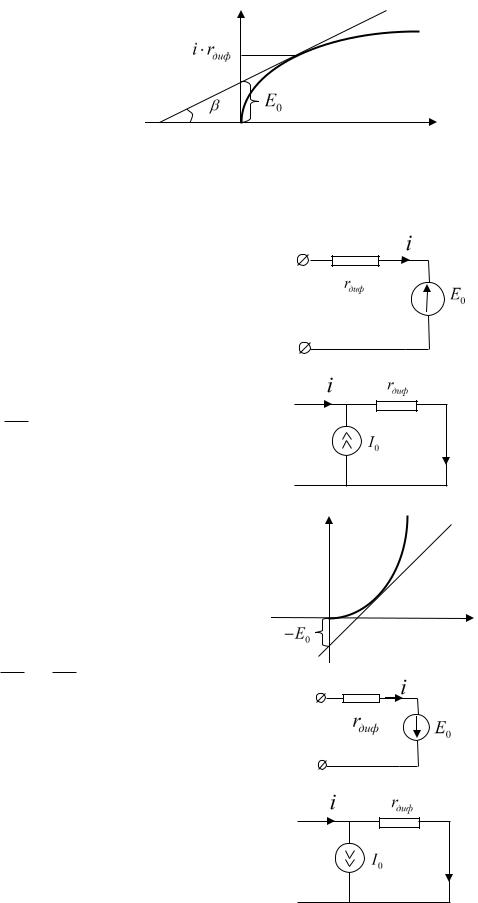
2.55. Графо-аналитические методы.
Этот метод, как следует из названия,
совмещает элементы графического и |
U |
||||||
аналитического |
методов. |
ВАХ |
|
||||
нелинейных |
элементов должна |
быть |
|
||||
задана графиком. В данном методе |
|
||||||
главная |
проблема |
состоит |
в |
|
|||
определении |
|
рабочей |
точки. |
|
|||
Предположим, |
рабочую |
точку |
нам |
I |
|||
определить |
|
удалось. |
Как |
нам |
уже |
|
|
известно,
rдиф k tg .
Тогда напряжение на нелинейном элементе в окрестности рабочей точки будет описываться выражением:
U E0 i rдиф ,
где E0 - напряжение на нелинейном элементе в отсутствие
тока, что соответствует эквивалентной схеме, изображенной на рисунке. Разделив полученное выражение на rдиф ,
получим ток через нелинейный элемент:
I |
U |
|
E0 |
i . |
|
|
|||
|
rдиф |
|
rдиф |
|
Вводя обозначение |
E0 |
I |
0 |
, получим, что i I I |
0 |
, что |
|
|
rдиф |
|
|
|
I |
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
соответствует эквивалентной схеме с источником тока. |
|
||||||
Однако ВАХ нелинейного элемента может иметь вид, |
|
||||||
сходный, например, с характеристикой диода, т.е. |
|
для |
U |
||||
данной характеристики касательная в рабочей точке |
|
||||||
пересекает ось напряжений в точке E0 . В этом случае |
|
||||||
эквивалентные схемы строятся точно так же с точностью |
|
||||||
до направления полярности источника E0 и I0 : |
|
|
|
||||
U E0 i rдиф . |
|
|
|
||||
Для схемы с источником тока: |
|
|
I |
||||
|
|
|
|||||
I |
U |
E0 i |
|
|
|
||
|
rдиф |
rдиф |
|
|
|
||
|
E0 |
I |
|
|
i I I |
|
. |
|
rдиф |
0 |
0 |
||||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
Эквивалентные схемы для обоих случаев изображены на |
|
||||
рисунках ниже. |
|
|
|
|
|
Итак, определим порядок расчета нелинейных элементов |
|
||||
графо-аналитическим методом: |
|
|
|
||
|
определяем рабочую точку; |
|
|
|
|
|
строим |
линеаризованную |
схему |
замещения |
I |
|
нелинейного элемента; |
|
|
||
|
|
|
|
||
|
проводим расчет для линейного участка любым |
|
|||
|
известным методом. |
|
|
|
|
70
