
Шпаргалки (фу!) / МП 2 курс / шпора
.pdf
Полученный |
результат |
также |
соответствует |
|
||||
результату, полученному ранее для частного |
|
|||||||
примера. |
|
|
|
|
|
|
|
|
Если мы теперь посмотрим на уравнение |
|
|
|
|
||||
|
|
|
|
|
|
|
|
, |
|
|
|
Yузловые |
|
J |
узловые |
||
где в J |
|
могут входить как источники тока, так и источники ЭДС, умноженные на |
||||||
|
узловые |
|
|
|
|
|
|
|
проводимость, |
Yii - собственные проводимости, берутся со знаком « + », Yij - взаимные |
|||||||
проводимости, берутся со знаком « – ». |
|
|
|
|
|
|||
Получим эту же систему уравнений в стандартном виде, т.е. через стандартную ветвь. Для стандартной ветви:
I i j
U e E .
Опираясьна закон Ома и записанные выше уравнения, получим:
I i j Y U Y e Y E .
Вспомним про редуцированную матрицу инциденций, умножим правую и левую часть на
A :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A Y |
e |
|
|
A |
|
I |
|
Y |
|
E |
|
|
A i |
|
0 по первому закону Кирхгофа
Сравниваем число уравнений и число неизвестных. Матрица A дает нам N-1 уравнений,
а число неизвестных – это число ветвей графа. Вспоминаем, что
A T e
Подставляем это в полученное ранее выражение:
A Y A T A I Y E
матрица узловых |
матрица токов в узлах |
проводимостей |
Jузлов |
|
Свели уравнение к полному. Получаем относительно :
A Y A T 1 A I Y E
Теперь можем найти все необходимое:
e A T ,U e E
i A Y e A I Y Ej i I
Замечание: Матрица A не требует составления дерева, поэтому вычислительный алгоритм для машин будет относительно простым.
21
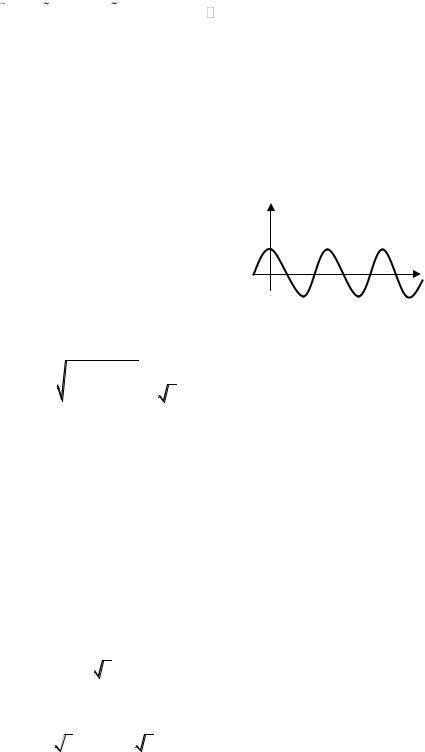
22. Расчет цепей на синусоидальном токе.
Переменными называются токи и напряжения, изменяющиеся во времени. Токи и напряжения, значения которых повторяются через определенное время,
называются периодическими:
i(t) f (t) f (t T ) f (t kT ), |
k , |
где Т – минимальный промежуток времени, через которое это равенство выполняется –
период. Величина f |
1 |
частотой. Величина 2 f |
2 |
называется циклической |
|
T |
T |
||||
|
|
|
частотой.
Преимущество синусоидальных токов:
1.при трансформации форма токов и напряжений не меняется;
2.реакцией цепи на синусоидальное воздействие является синусоидальная функция той же частоты (доказательство этого утверждения оставим на первый семестр);
3.нет помех радиоприему.
Частными |
случаями периодических переменных функций |
i |
||
являются синусоидальные функции: |
|
|||
|
|
|||
|
i(t) Im sin( t i ) , |
|
|
|
|
u(t) Um sin( t u ) . |
|
t |
|
|
|
|
||
Рассмотрим некоторые параметры синусоидальных функций. |
|
|||
Очевидно, |
синусоидальная |
функция |
характеризуется |
|
максимальным значением Im , |
частотой |
и сдвигом фаз i . Есть еще одна |
||
характеристика синусоидальной функции – ее действующее значение:
|
|
|
|
1 |
T |
|
|
I |
m |
|
I |
|
I |
|
0 |
i2 (t)dt |
|
||||
ä |
T |
|
|
|
||||||
|
2 |
|||||||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||
Теперь поясним выше сказанное, отдельно взяв интеграл под корнем:
|
|
1 |
|
T |
i2 |
(t)dt |
1 T |
I |
2 sin2 |
( t)dt |
|
I |
m |
2 |
|
T 1 cos 2 t |
dt |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
T 0 |
T 0 |
|
|
|
|
0 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
m |
|
|
|
T |
|
|
2 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
Im2 |
T |
1 |
|
Im2 |
T cos 2 t d 2 t |
Im2 |
|
Im2 |
sin 2 t |
|
T0 |
|
Im2 |
. |
|||||||||||||||
|
||||||||||||||||||||||||||||||
T |
2 |
4 t |
|
4 t |
2 |
|||||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||
ВНИМАНИЕ: Амперметр всегда показывает действующее значение.
Введем понятие среднего значения – средневыпрямленное за период значение функции.
|
|
2 |
T |
|
|
2 |
|
|
|
|
T |
|
2 |
|
|
0 |
|
1 |
|
|
|
2 |
|
|
|
|||
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 1)) |
|
|
|
|||||||||
|
|
|
2 I |
|
sin t dt |
|
I |
|
cost |
|
2 |
|
|
I |
|
cost |
|
|
|
(1 cos |
|
|
I |
|
. |
|||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
ñð |
|
T 0 |
m |
|
T |
|
m |
|
|
0 |
|
T |
|
m |
|
|
|
|
|
2 |
|
|
|
m |
|
|||
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||||||
Рассмотрим коэффициенты, характеризующие синусоиду:
коэффициент амплитуды:
|
|
|
|
|
|
Im |
|
|
|
|
1, 41. |
|||||||||
|
|
|
K |
a |
2 |
|||||||||||||||
|
|
I |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
коэффициент формы: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
|
|
I |
|
I |
m |
|
|
|
|
|
|
|
|
|
|
1,11. |
|||
ф |
Iф |
|
|
|
2Im |
|
|
|
||||||||||||
|
|
|
||||||||||||||||||
|
|
|
2 |
|
|
|
|
2 |
2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
Поскольку частоты воздействия и реакции цепи одинаковы, при решении задач нас будут интересовать амплитудные значения и сдвиги фаз.
22
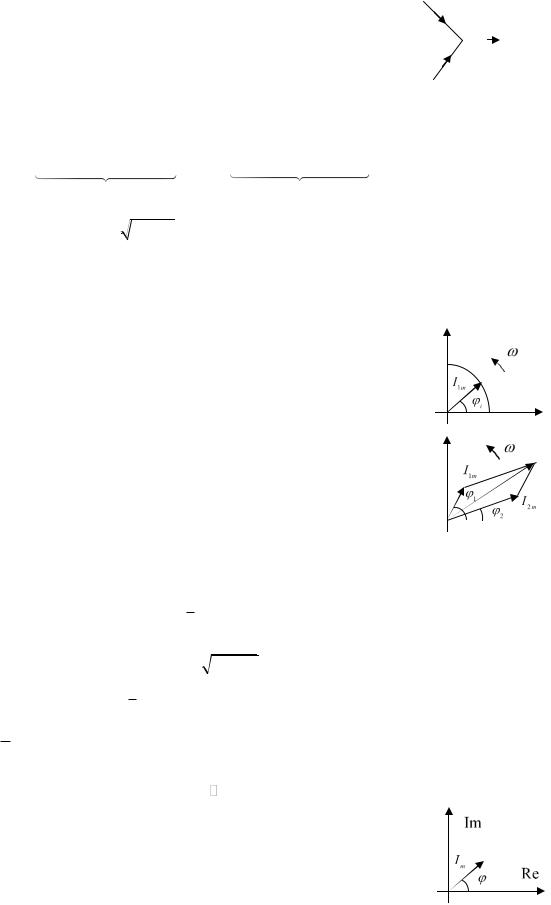
23. Изображение синусоидальных величин векторами и комплексными числами.
Итак, наша задача – найти амплитудные значения и начальные фазы всех токов и напряжений. Воспользовавшись непосредственно законами Кирхгофа, получим систему интегро-дифференциальных уравнений, которая решается достаточно сложно. До
проведения каких-либо расчетов посмотрим, почему возникает задача представления |
||||||||||||
векторов в виде комплексных чисел. |
|
|
|
|
|
|
|
|||||
Рассмотрим следующую задачу (см. рисунок). Даны два тока: |
i1 |
|
||||||||||
|
i (t) I |
sin( t ) |
|
|
|
|
i3 |
|||||
|
|
|
|
|
|
|||||||
|
1 |
|
1m |
|
|
1 |
|
|
|
|
|
|
i2 (t) I2m sin( t 2 ) |
|
|
|
|
i2 |
|
||||||
|
|
|
|
|
||||||||
Наша задача – найти i3 (t) I3m sin( t 3 ) . |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
i3 (t) i1 (t) i2 (t) Im1 sin( t 1) Im2 sin( t 2 ) |
|
|
||||||||||
I1m sin t cos 1 I1m cos t sin 1 |
I2m sin t cos 2 I2m cos t sin 2 |
|
|
|||||||||
Im cos 1 I2m cos 2 sin t (I1m sin 1 I2m sin 2 ) cos t , |
|
|
||||||||||
|
|
a |
|
|
|
|
|
b |
|
|
||
тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
arctg |
b |
. |
|
|
I |
3m |
|
a2 |
b2 |
|
3 |
|
|
||||
|
|
|
||||||||||
|
|
|
|
|
|
|
a |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
Решение достаточно простой задачи, где мы не имели дело с индуктивностями и емкостями, выглядит весьма громоздко. Поищем другой способ решения данной задачи.
Заметим, что наш ток i1 t мы можем изобразить в виде вращающегося на плоскости против часовой стрелки вектора, обладающего длиной I1m , частотой
вращения и начальный угол отклонения от горизонтальной оси i .
Тогда проекция этого вектора на вертикальную ось как раз будет изменяться по закону (см. рисунок):
i1 (t) I1m sin( t 1 ) .
Тогда мы можем легко применить первый закон Кирхгофа к двум токам из нашей задачи: задача сложения токов сводится к сложению двух векторов (см. рисунок ниже). Такой подход к решению задачи допустим, потому что все три вектора (и исходные, и результирующий) будут вращаться на плоскости с одной и той же угловой частотой, взаимное расположение
векторов в любой момент времени остается постоянным.  Совокупность векторов, отображающих синусоидальные токи и напряжения, построенных с учетом относительной ориентации и масштабов, называется векторной диаграммой. Проводим аналогию с обобщенным комплексным воздействием. Рассмотрим комплексное число:
Совокупность векторов, отображающих синусоидальные токи и напряжения, построенных с учетом относительной ориентации и масштабов, называется векторной диаграммой. Проводим аналогию с обобщенным комплексным воздействием. Рассмотрим комплексное число:
A a jb ,
тогда модуль этого числа:
A 
 a2 b2 ,
a2 b2 ,
тогда мы можем записать:
A Aei Acos jAsin ,
где arctg ba . Возьмем нашу синусоидальную функцию и поставим ей в соответствие комплексное число:
i(t) I |
m |
sin( t ) |
I |
m |
e j ( t ) I |
m |
e j e j t . |
|
|
|
|
|
Мы знаем, что
23

e j cos j sin ,
т.е. эта величина определяет начальный сдвиг фаз на комплексной плоскости. Рассмотрим фактор e j t :
e j t cos t j sin t .
Это единичный вектор, который определяет направление вращения вектора тока на комплексной плоскости против часовой стрелки с угловой скоростью . Можно записать еще и следующим образом:
|
|
|
i(t) I |
m |
sin(t ) |
I |
m |
e j ( t ) I |
m |
e j t , |
|
|
|
|
|
|
|
|
|||
где I |
m |
e j |
- комплексная амплитуда. |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Величины, зависящие от времени: токи, напряжения, значения источников ЭДС и тока изображаются на комплексной плоскости векторами и обозначаются I , U , E, J ( с
точкой). Величины не зависящие от времени (сопротивление,..), отображаются
отрезками.
Если при решении задачи с помощью комплексных числе мы нашли комплексную амплитуду, то для нахождения временной функции мы обязаны помножить эту амплитуду
на e j t и взять от полученной величины мнимую часть:
Im((Ime j )e j t ) Im sin(t ) .
1)соответствие временных функций и комплексных величин (векторов), которое справедливо только для линейных цепей (принцип суперпозиции);
2)из двух составляющих - sin и cos - физическая реализация возможна только для синуса.
3)переход в область действительных времен (оригиналов) осуществляется путем выделения мнимой части.
24

24. Основная идея состояла в том, чтобы уйти от системы интегральных и дифференциальных уравнений. Путь у нас есть ток, у него есть отображение:
i t Im sin t |
Ime j e j t Ime j t , |
посмотрим, что происходит с его производной:
dit t Im cos t 1 .
Мы говорили, что переход осуществляется по синусу, поэтому
|
t |
|
2 . |
1 Im sin |
|
||
|
|
2 |
|
Теперь переходим в область комплексных времен (изображений):
|
|
t |
|
|
j |
|
|
2 |
j |
|
Ime j e j t e |
|
j Ime j t . |
||
Ime |
|
2 |
|
2 |
Вывод: В области комплексных величин операция дифференцирования заменяется умножением на фактор j .
Посмотрим теперь на интеграл:
|
I |
|
|
I |
|
|
|
|
I |
|
|
t |
|
|
I |
|
|
|
|
|
I |
|
|
i t dt |
m |
cos t |
m |
|
m |
j |
|
|
m |
j |
|
|
m |
|
|||||||||
|
|
sin |
t |
|
|
e |
|
2 |
|
|
e j e j t e |
|
2 |
|
|
e j t . |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
j |
|
|||||||
Вывод: В области комплексных величин операция интегрирования заменяется делением на фактор j .
Теперь ясно, что мы от системы интегро-дифференциальных уравнений можем уйти в область комплексных величин, решить задачу, а потом вернуться к область действительных функций путем выделения мнимой части.
Еще мы ранее говорили о системе вращающихся векторов: у них у всех одинаковая частота. В этом мы сейчас и убедились: действительно, у всех рассматриваемых векторов
есть множитель e j t – единичный вектор, обеспечивающий вращение всей системы против часовой стрелки с одной частотой. Значит мы может рассматривать только
взаимное расположение наших векторов на комплексной плоскости, а о факторе e j t нужно вспоминать только тогда, когда переходим в область действительных времен.
Расчет синусоидальных функций с использованием комплексных величин называется
комплексным или символическим методом.
25
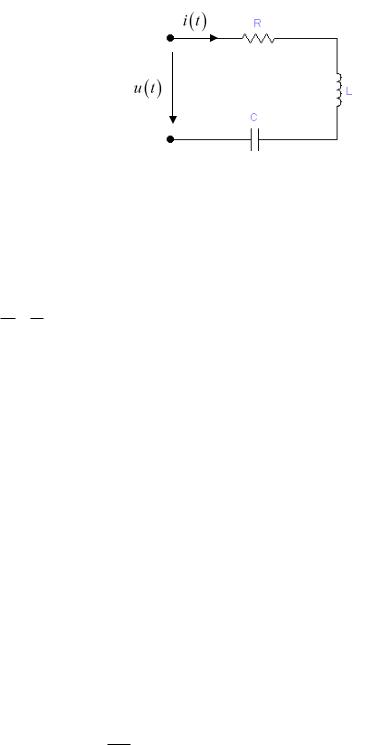
|
25. Задача. |
|
|
|
|
|
Возьмем RLC цепь (см. рисунок ниже). Известно, что |
|
|
|
|
|
|
|
u t Um sin t u . |
|
|
|
|
|
Нужно найти ток: |
|
|
|
|
|
|
|
i t Im sin t i |
|
|
|
|
|
|
|
R |
|
|
|
|
Частота тока и напряжения одна и та же, значит |
|
|
|
|
|
|
|
|
|
|
|
||
необходимо найти Im и i . |
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
L |
||
Выполним решение двумя способами: |
|
|
|
|
||
|
|
|
|
|
||
1) |
непосредственным интегрированием с |
|
C |
|
|
|
|
|
|||||
|
использованием заданных функций; |
|
|
|
|
|
|
|
|
|
|
|
|
2) |
символическим методом; |
|
|
|
|
|
1 способ:
Т.к. вектора тока и напряжения вращаются с одинаковой частотой, их взаимное расположение будет зафиксировано. Тогда пусть u i , и будем считать, что
u t Um sin t i t Im sin t .
Записываем второй закон Кирхгофа для цепи:
u t iR L di 1 t i d UC 0 . dt C 0
Здесь мы возьмем определенный интеграл, чтобы не выпускать начальные значения и смотреть, что происходит в цепи. Далее определенным интегралом пользоваться не будем (впоследствии будет показано, почему). Подставляем в это уравнение начальные:
U |
|
sin t I |
|
R sin t LI |
|
cos t |
1 |
I |
|
cos t |
Im |
U |
|
0 . |
m |
m |
m |
|
m |
C |
C |
||||||||
|
|
|
|
C |
|
|
|
|||||||
Мы уже говорили, что реакцией цепи на синусоидальное воздействие будет синусоидальное воздействие той же частоты. Поэтому в установившемся режиме (а мы
сейчас рассматриваем установившиеся режимы) сумма |
Im |
UC 0 0 . В общем случае |
|
C |
|||
|
|
эти слагаемые обусловлены переходным процессом. Казалось бы, вполне естественно
t |
|
писать определенный интеграл i d . Но |
UC 0 - некая «предыстория», это |
0 |
|
напряжение, которое имеется в нулевой момент времени на конденсаторе (это напряжение появляется в результате переходного процесса, по сути UC 0 - интеграл от до 0 ).
Итак, к этому материалу мы вернемся в следующем семестре, а пока будем писать неопределенный интеграл. Теперь решим получившееся уравнение, взяв два удобных момента времени:
1) t 0 :
Um sin LIm Im ;
C
2) t 2 :
Um cos Im R ;
Получили два уравнения с двумя неизвестными. Решаем:
26
1 |
2 |
2 |
2 |
|
|
2 |
|
|
|
1 |
|
2 |
|
|
Um Im R |
|
|
L |
|
|
|
|
|||
|
|
|
C |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||
Сдвиг фаз находим делением 1 / 2 : |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
L |
1 |
||
|
|
|
|
|
arctg |
C |
||||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
R |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
|
Im |
|
|
|
|
Um |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
||||||
|
|
|
|
2 |
|
|
|
1 2 |
|||
|
|
|
R |
|
|
L |
|
|
|
||
|
|
|
|||||||||
|
|
|
|
|
|
|
|
C |
|||
.
Из этого уравнения следует, что угол сдвига фаз между током и напряжением определяется только параметрами самой цепи.
Вернемся к первоначальному уравнению для этой задачи и посмотрим размерность:
U |
|
sin t |
I |
|
|
R |
sin t LI |
|
cos t |
1 |
I |
|
cos t |
Im |
U |
|
0 |
, |
|
m |
m |
m |
|
m |
C |
C |
|||||||||||||
|
|
|
|
|
|
|
C |
|
|
|
|
||||||||
Вольт |
|
Ампер Ом = |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Вольт |
|
|
|
|
|
|
|
|
|
|
|
|
||||
получаем, что L X L |
и |
|
|
1 |
|
XC - реактивные X |
|
|
|
|
|
|
|
|
|
||||
C |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
сопротивления – сопротивления индуктивности и емкости на переменном токе, измеряются, как и активные сопротивления, в Омах. График зависимости реактивных сопротивлений от изображен на рисунке.
2 способ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теперь те же самые выражения получим |
|
|
|
|
|
|
|||||||||||||||||
символическим методом: |
|
|
|
|
|
|
|
|
|
|
1 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
U |
m |
sin |
|
t |
u |
|
U |
m |
e j t |
|
Im Re j t j LIme j t |
|
Ime j t Ume j t . |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
I sin t |
|
I e j t |
j C |
||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
m |
|
|
|
|
i |
|
|
m |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Видно, что все вектора вращаются с одной частотой, |
у всех величин будет фактор e j t . |
||||||||||||||||||||||
Тогда, сокращая на e j t |
и вынося I |
m |
в левой части за скобку, получим: |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Um Im R j L |
|
|
Im Z , |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где Z R j L |
|
|
|
|
- комплексное сопротивление цепи. |
|
|
||||||||||||||||
C |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ВАЖНО!!!
Здесь Z именно неперечеркнуто!!! Z будет иметь другой смысл: Z Z
При этом комплексное сопротивление индуктивности и емкости соответственно имеют вид:
ZL |
jL jX L , |
|||||
Z |
|
|
j |
|
j |
. |
C |
|
|
||||
|
|
C |
XC |
|||
|
|
|
||||
Комплексные величины равны тогда и только тогда, когда равны их амплитуды и фазы:
U |
|
I |
Z |
|
I |
|
|
Um |
|
|
|
|
|
Um |
|
|
|
|
|
, |
m |
m |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
m |
|
|
|
|
Z |
|
|
|
|
1 |
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
|
|
27
|
|
|
L |
1 |
|
|
|
|
|
C |
|
||
|
|
|
arctg |
|
. |
|
u |
|
|
||||
|
i |
|
R |
|
|
|
|
|
|
|
|
|
|
Посмотрим на реактивные сопротивления, на uL и uC . Пусть для тока есть
i t Im sin t |
Ime j t , |
тогда для индуктивности:
uL L didi j LIm
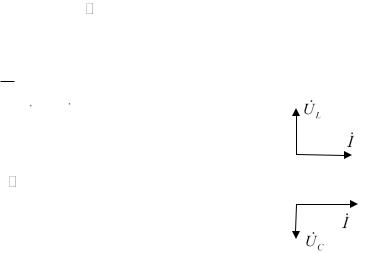
Из последнего уравнения следует, что U L и I будут располагаться так, как
j
показано на рисунке (действительно, j e 2 ). Аналогично для емкости:
u |
1 |
|
i t dt |
Im |
j |
Im |
. |
C |
|
|
|||||
c |
|
j C |
|
C |
|||
|
|
|
|||||
Тогда вектор напряжения относительно вектора тока будет направлен вниз (см. рисунок).
Итак, если вращение вектора тока и вектора напряжения по кратчайшему пути происходят против часовой стрелки, то такой угол сдвига фаз является положительным, если по часовой стрелке – отрицательным.
28
27. Мощности в цепях синусоидального тока.
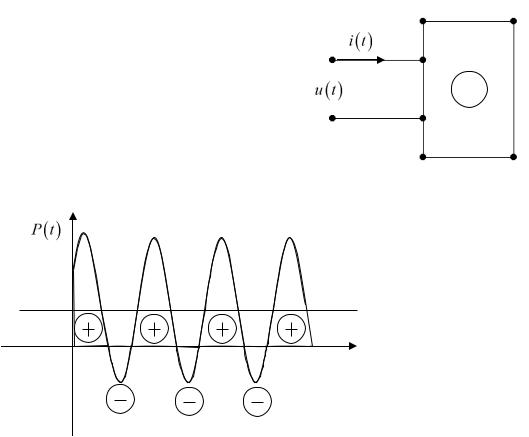
Пусть у нас есть пассивный двухполюсник, есть входной ток и входное напряжение:
i t Im sin t ,
u t Um sin t .
Как мы знаем, мгновенная мощность: |
|
|
|
|
П |
|||||||||
|
|
|
|
|
||||||||||
|
|
p t i t u t Im sin t Um sin t |
|
|
||||||||||
|
ImUm |
|
cos cos |
|
2 t |
|
IU |
|
cos cos |
|
2 t |
|
, |
|
2 |
||||||||||||||
|
|
|
|
|
|
|
||||||||
где I |
и U - действующее значения. Посмотрим теперь |
|
|
|||||||||||
график мгновенной мощности: |
|
|
|
|
|
|
|
|||||||
t
Есть некая средняя линия IU cos (пунктир), не зависящая от времени, и
накладывающаяся на нее периодическая функция, причем обладающая удвоенной частотой по отношению к внешнему воздействию и реакции цепи. Положительное
значение p t («положительная» площадь) говорить нам о том, что ток и напряжение совпадают по фазе, и источник отдает энергию в нагрузку. Отрицательное значение p t
обусловлено возвращением энергии, накопленной элементами цепи в электрическом и магнитном поле, в источник.
t
p t dt - энергия, которая закачивается источником в нагрузку. Определим активную
0
мощность – среднюю за период энергию, передаваемую от источника в нагрузку:
|
1 |
T |
|
P |
p t dt . |
||
T |
|||
|
0 |
||
|
|
Эта мощность измеряется в Âò - Ваттах. Определение справедливо для периодического
как синусоидального, так и несинусоидального воздействия. Для синусоидального тока имеем:
P IU cos .
Это не определение мощности, это следствие из общего определения, записанного чуть выше.
Посмотрим, в каких пределах может меняться . Т.к. двухполюсник у нас пассивный,
мощность он только потребляет (действующие значения тока и напряжения положительны по определению). Тогда
29
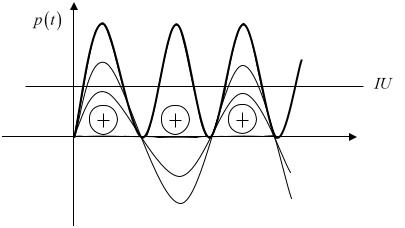
P 0 |
|
cos 0 |
|
|
|
|
. |
|
|
|
|
|
2 |
|
2 |
Посмотрим теперь мощности на активном сопротивлении, на индуктивности и на емкости.
1) активное сопротивление;
i t Im sin t
p t IU cos IU cos 2t .
Ток и напряжение по фазе совпадают, 0 , активная мощность p IU , тогда p t IU IU cos 2t
Построим график:
t
Причем всегда P 0 . Действительно, из энергетических соображений: не происходит накопления энергии в магнитном и электрическом полях, а сопротивление всегда потребляет мощность.
2) индуктивность;
i t Im sin t
|
t |
|
u t LIm cost LIm sin |
. |
|
|
|
2 |
Посмотрим на физический смысл p t :
p t i t u t i t L |
di |
|
d |
i2 |
|
d |
Wмагн |
||
|
|
L |
|
|
|
||||
|
|
|
|
||||||
|
dt |
|
dt |
2 |
|
|
dt |
|
|
Мгновенная мощность равна скорости изменения энергии, запасаемой в магнитном поле катушки. Из обсуждаемой выше векторной диаграммы тока и напряжения на
индуктивности, 2 , тогда
p t IU sin 2 t .
30
