
Шпаргалки (фу!) / МП 2 курс / шпора
.pdf
1. Электрической цепью называется система заряженных частиц и проводников с током, которые могут быть описаны такими интегральными понятиями, как ток (I), напряжение
(U), ЭДС E , мощность Р и энергия W , или для мгновенных значений i t , |
u t , |
t , p t и w t соответственно. |
|
Элементы цепи – то из чего состоит цепь; они призваны отображать одно из нескольких свойств:
1)генерировать энергию или преобразовывать другие виды энергии в электрическую;
2)рассеивать энергию;
3)накапливать энергию в магнитном поле;
4)накапливать энергию в электрическом поле.
Понятно, что реальные элементы каким-либо одним свойством обладать не могут (катушка индуктивности – это и провод (сопротивление), и индуктивность; а так как работаем на высоких частотах, возникает еще и межвитковая емкость. Итого – 2, 3 и 4 пункты). Мы будем использовать математические модели элементов.
Классификация элементов.
Элементы бывают:
1)линейные (с постоянными параметрами) и нелинейные (с параметрами, зависящими от токов и напряжений); соответственно различают линейные и нелинейные цепи;
2)элементы с параметрами, зависящими от времени – параметрические элементы; иначе элементы называют время-инвариантными.
3)Элементы с сосредоточенными параметрами – если ток через любое сечение
элемента неразветвленной ветви в любой момент времени t остается постоянным, т.е. i1 t i2 t i t . Если же ток зависит от координаты, то имеем дело с
элементами с распределенными параметрами.
Конечно, элементы могут комбинировать несколько свойств (линейные с сосредоточенными параметрами и т.п.).
Любая часть цепи, содержащая 2 зажима, называется двухполюсником. Двухполюсники бывают активные и пассивные. Пассивным принято считать двухполюсник, для которого
t |
|
|
|
w t u i d 0 t . |
П |
|
А |
|
|
|
|
|
|
|
|
|
|
|
Математическое определение: активный двухполюсник содержит в своем составе нескомпенсированные источники энергии; пассивный не содержит источников энергии, либо они взаимно скомпенсированы.
1
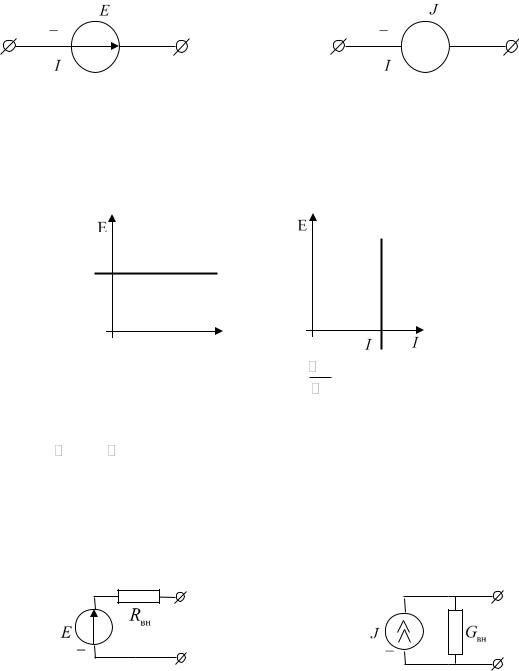
2. Элементы, генерирующие энергию.
Идеальный источник ЭДС |
Идеальный источник тока |
+ |
+ |
>>
Основные свойства:
разность потенциалов на зажимах идеального источника ЭДС не зависит от величины и направления протекающего тока;
величина и направление тока в ветви с идеальным источником тока не зависит от разности потенциалов на зажимах источника.
Вольт-амперные характеристики идеальных источников:
0 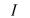 0
0
Еще одна характеристика двухполюсника - Rвн UI . Для идеального источника ЭДС
имеем: ток может иметь конечное приращение, а разность потенциалов = 0, поэтому Rвнутр 0 . Для идеального источника тока – наоборот: внутреннее сопротивление
Rвнутр , т.к. |
I 0 , |
U const . |
Неидеальные (реальные) источники тока и ЭДС.
Реализовать идеальный источник тока или ЭДС на практике невозможно. Значит, неидеальные источники тока и ЭДС будут выглядеть следующим образом:
Неидеальный источник ЭДС |
Неидеальный источник тока |
+ |
+ |
|
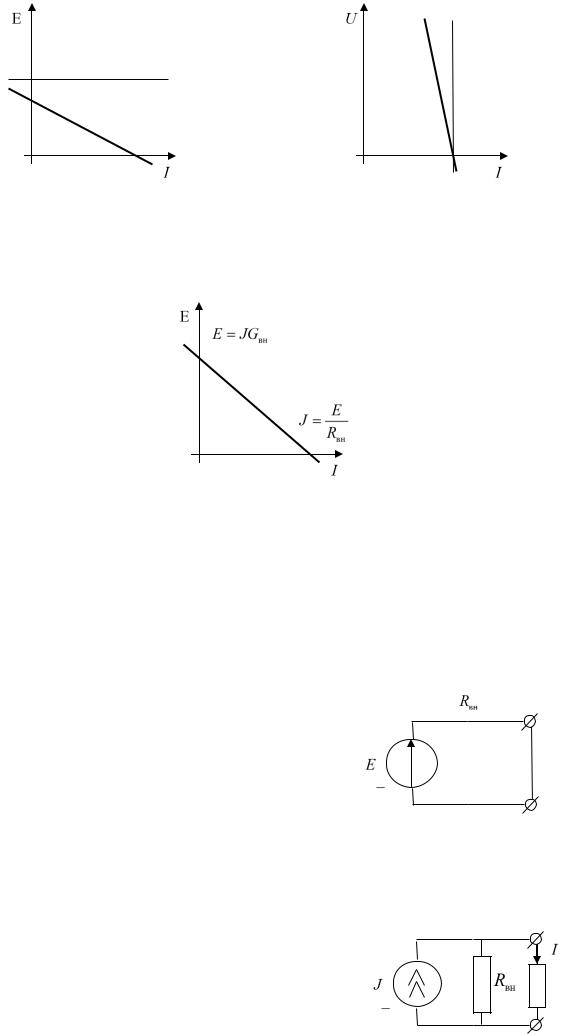
Посмотрим, как изменятся вольт-амперные характеристики. Теперь для неидеального источника ЭДС в зависимости от протекающего тока разность потенциалов будет меняться. Очевидно, будет наблюдаться падение напряжения (ток через внутреннее сопротивление течет от + к –). Значит и характеристика будет падающей. Аналогично для неидеального источника тока, падение напряжение будет происходить на внутренней проводимости.
2
0 |
0 |
Заметим, что характеристики неидеальных источником тока и ЭДС практически ничем не отличаются, разве что наклоном к вертикали. Этого достаточно, чтобы преобразовать неидеальный источник ЭДС в неидеальный источник тока, и наоборот. Построим по двум известным точкам (значения тока и напряжения на координатных осях) общую прямую для неидеальных источников:
0
При совпадении характеристик мы получаем, что Gвн Rвн . Т.е. мы можем преобразовать
неидеальный источник ЭДС в неидеальный источник тока, и наоборот. Идеальный источник тока к идеальному источнику ЭДС и наоборот преобразовать невозможно.
Это есть пример эквивалентного преобразования элементов. Преобразование считается эквивалентным, когда для внешней цепи токи, напряжения и мощности (внешние характеристики) сохраняются. С внутренними дело обстоит несколько по-другому. Рассмотрим этот случай.
Возьмем цепи, состоящие из неидеальных источников (тока и напряжения) и нагрузки.
В |
случае |
|
для источника |
ЭДС |
ток |
через нагрузку |
|
|
|
|
|
||
I |
|
E |
, |
значит, мощность, которая |
выделяется на |
+ |
|
|
|
|
|||
|
|
|
|
||||||||||
|
|
|
|
|
|
||||||||
|
R Rвн |
|
|
|
R |
||||||||
|
|
|
|
|
|
|
|
|
|
||||
нагрузке, равна: |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
P I 2 R |
E2 R |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
R R |
2 |
|
|
|
|
|
|
||
|
|
|
|
R |
|
|
|
|
|
|
|
||
|
|
|
|
|
вн |
|
|
|
|
|
|
|
|
Теперь рассмотрим аналогичную схему с источником
тока. По нашему эквивалентному преобразованию,
+
R
3
J |
E |
. Тогда ток, который будет протекать через |
|||||||
|
|||||||||
|
Rвн |
|
|
|
|
|
|
||
нагрузку, будет равен |
|
|
|
|
|
|
|||
|
|
IR J Rвн / R Rвн |
|
E |
. |
|
|
||
|
|
|
|
|
|
|
|||
|
|
R Rвн |
|
|
|||||
|
|
|
|
|
|
||||
Тогда для мощности получаем: P E2 |
R |
|
|
|
|||||
|
|
|
|
|
|||||
R R |
2 |
||||||||
|
|
R |
|
||||||
|
|
|
|
|
|
вн |
|
|
|
Т.е. при таком изменении сохранились напряжение и мощность на нагрузке.
Посмотрим, что происходит с внутренними соотношениями. Для этого вычислим мощность, выделяющуюся на внутреннем сопротивлении источников.
В первом случае (для источника ЭДС " E "):
|
|
P |
I |
2 R |
E2 |
Rвн |
|
|
|
|
|
|
|
||||
|
|
R+R |
|
2 |
|
|
|
||||||||||
|
|
|
вн |
|
|
вн |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
вн |
|
|
|
|
|
|
|
Во втором случае (для источника тока " J ") |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
JR |
|
2 |
|
|
|
|
R |
2 |
|
Rвн |
|
||
Pвн |
IR2 Rвн |
|
|
|
|
Rвн |
E2 |
|
|
|
|
||||||
|
|
|
|
|
R R |
2 |
|||||||||||
|
вн |
|
R Rвн |
|
|
|
Rвн |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вн |
|
Если R Rвн , то внутренние соотношения при эквивалентном преобразовании цепей в общем случае не сохраняются.
4
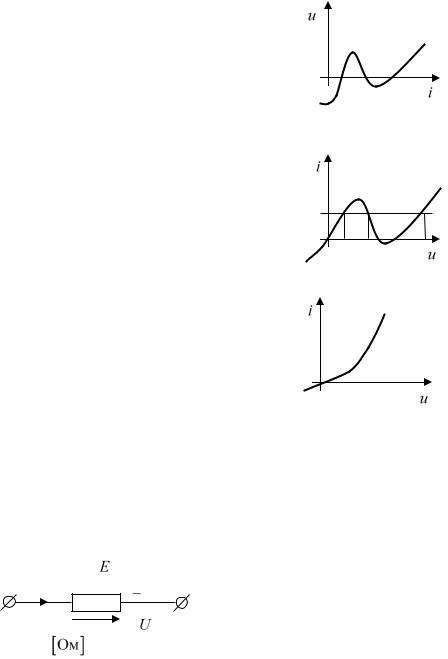
3. Элементы, рассеивающие энергию.
Резисторы.
Любой двухполюсник называется двухполюсником резистивного типа, если ток и
напряжение на нем связаны соотношением f i t ,u t ,t 0 , где |
f - алгебраическая |
|
|
|
|
функция, т.е. не содержащая производных и интегралов.
Источник ЭДС – элемент резистивного типа.
Исходя из определения, двухполюсник резистивного типа может быть задан своей вольтамперной характеристикой. В зависимости от видов характеристик, существует несколько классификаций двухполюсников резистивного типа.
1. u t f i t ,t |
- резистивный элемент, управляемый током. В |
|
|
|
|
этом случае:
для любого i из области определения f существует одно и
|
только одно значение напряжения; |
|
|
|||
|
второй |
параметр |
t говорит |
о том, что |
резистивный |
|
|
двухполюсник может быть параметрическим. |
|
||||
2. |
i t g u t ,t |
- |
резистивный |
элемент, |
управляемый |
|
|
|
|
|
|
|
|
напряжением.
(пример – туннельный диод). Он не является управляемым током, поскольку существует более одного значения напряжения для одного значения тока.
3. Монотонный элемент – двухполюсник резистивного типа, управляемый одновременно и током, и напряжением. Пример – характеристика обычного диода:
|
i t |
e u t |
1 |
u t |
1 |
ln |
|
i t |
1 |
|
|
||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
Это означает, |
что |
f u t ;i t ;t 0 |
- |
|
обратима, т.е. существует обратная |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
g u t ;i t ;t 0 , которая определена однозначно. |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Важным |
частным |
случаем |
является |
линейный |
резистивный |
двухполюсник: |
|||||||
u t R t i t , |
или для время-инвариантных элементов, |
u t Ri t |
- закон Ома для |
||||||||||
линейного время-инвариантного резистора.
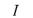 +
+
5
4. Двухполюсник индуктивного типа.
Они призваны накапливать энергию в магнитном поле. Характеризуются двухполюсники
индуктивного типа магнитным потоком Ф t .
коэффициентом L , то |
говорим |
о линейном |
||||
индуктивного типа. |
|
|
|
|
||
u t |
dФ t |
L |
di |
, |
и обратно: |
|
dt |
dt |
|||||
|
|
|
|
|||
Если Ф I с неким постоянным время-инвариантном двухполюснике
i t 1 t u d i0 L 0
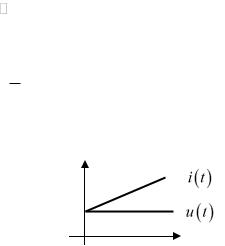
Вопрос: может ли на зажимах линейного время-инвариантного двухполюсника индуктивного тока поддерживаться постоянное напряжение, отличное от нуля?
Решение: если у нас есть постоянное напряжение, то ток будет линейной характеристикой (см. рисунок). Если мы сумеем обеспечить нарастание тока по линейному закону (например, переходной процесс: суперпозиция экспонент, разложение в ряд, первые два члена которого будут содержать только нулевую и первую степень аргумента –линейная функция – но это для начального момента времени, переходного процесса!), то и напряжение на зажимах будет постоянным.
Ответ: может.
Вопрос: может ли на зажимах линейного время-инвариантного двухполюсника индуктивного тока поддерживаться постоянное напряжение в установившемся процессе? Ответ: не может.
Нужно внимательно следить за постановкой вопроса, особенно на экзамене
Из полученных выше соотношений следует, что индуктивность является дифференциатором тока (производной по току) и интегратором напряжения. Единицы измерения индуктивности – Генри.
6

5. Емкость.
Характеристикой емкости является заряд. Если заряд пропорционален напряжению с некоторым постоянным коэффициентом С, то имеем дело с линейным времяинвариантным двухполюсником емкостного типа:
q Cu
Известно, что i t |
dq t |
, i t C |
dUC |
dt |
dt |
UC t 1 t i d U0 C 0
Тот же вопрос: может ли через емкость протекать постоянный ток?
Ответ: может, если мы обеспечим линейно возрастающее напряжение в переходном процессе. В постоянном режиме – не может.
Емкость является дифференциатором напряжения и интегратором тока
7
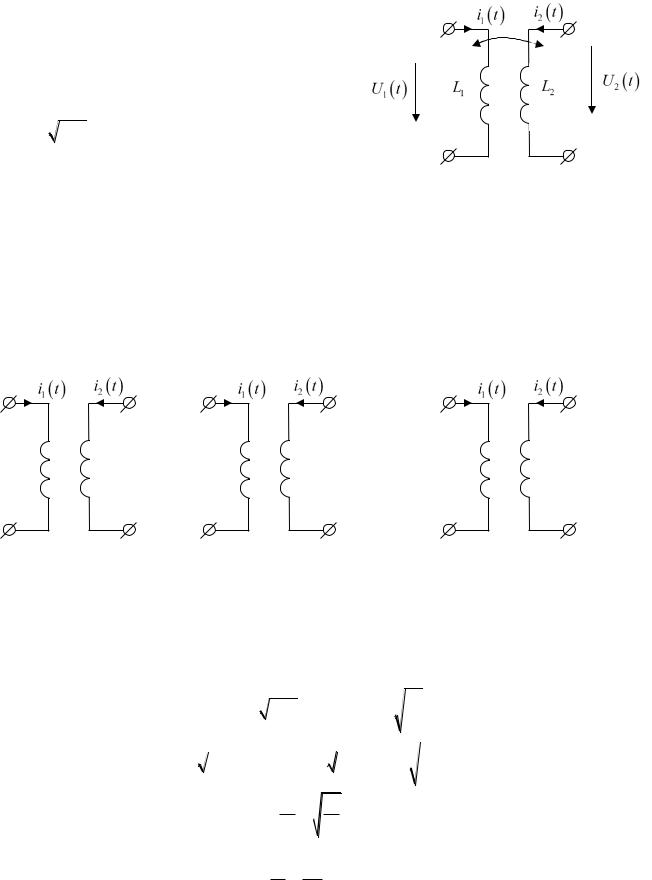
6. Взаимная индуктивность.
Это уже не двухполюсник, а четырехполюсник: 2 входных и 2 выходных зажима. * * - одноименные зажимы.
|
|
U |
t L |
di1 |
|
M |
di2 |
|
|
вход |
|||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
||||||||
|
|
|
1 |
1 |
|
dt |
|
|
dt |
|
|||
|
|
U |
|
t L |
|
di2 |
M |
di1 |
|
|
|||
|
|
|
|
|
|
||||||||
|
|
|
2 |
2 |
|
dt |
|
|
dt |
|
|||
Коэффициент взаимной индукции: |
|
||||||||||||
|
|
|
|
|
|
|
|||||||
M K L1L2 , где K |
- |
|
коэффициент связи, |
|
|||||||||
лежащий в диапазоне 0;1 ; |
выход |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* 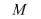 *
*
если K 0 , то имеем дело с несвязанными индуктивностями;
если K 1 (полная связка), то имеем дело с идеальным трансформатором.
Если входной и выходной токи втекают или вытекают из одноименных зажимов, то имеем дело с согласным включением. Иначе – встречное включение (на рисунках ниже
i1 t - входной ток, i2 t - выходной ток). Т.е. если сначала и входной, и выходной токи
сначала проходят зажим, а затем заходят в катушку (сначала оба проходят катушку, а потом оба входят в зажим), то речь идет о согласном включении. В противном случае (один из токов втекает в зажим, а потом идет в катушку, а другой, наоборот, сначала проходит катушку, а потом – в зажим), то имеем дело со встречным включением.
Согласное Встречное
* |
* |
или |
|
* |
|
|
|
|
|
|
|
* |
* |
* |
|
|
|
При согласном включении слагаемое со взаимной индуктивностью имеет тот же знак, что и слагаемое с собственной индуктивностью (а знак перед этим слагаемым зависит от условного направления тока в данной индуктивности). При встречном включении – наоборот, знаки противоположны.
Соотношение для идеального трансформатора.
Возьмем согласное включение.
|
|
|
|
|
|
|
|
|
|
|
|
|
di |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
t L1 |
di |
|
|
|
|
|
di |
L1 |
|
|
|
L |
|
|
|
di |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
u1 |
|
1 |
|
L1L2 |
|
|
2 |
|
|
|
1 |
|
|
2 |
|
|
2 |
|
|
; |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
dt |
|
|
|
|
|
dt |
|
|
dt |
|
|
|
L1 |
|
|
|
dt |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
di |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
di |
|
|
di |
|
|
|
|
|
|
|
|
|
L di |
|
|
|||||||||||||||
u2 t L1L2 |
L2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
1 |
|
2 |
|
L1L2 |
|
|
1 |
|
2 |
|
|
|
2 |
|
. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
dt |
|
|
dt |
|
|
|
|
|
|
dt |
|
|
|
|
L1 |
dt |
|
|||||||||||||
u1 L1 u2 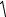 L2
L2
Как известно, индуктивность катушки прямо пропорциональна квадрату числа витков W :
u1 W1 n , u2 W2
n - коэффициент трансформации.
8
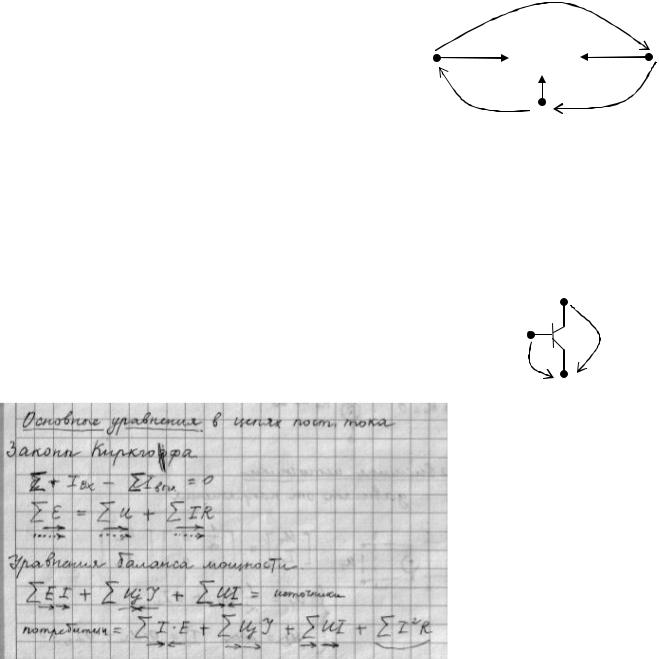
7. Многополюсник.
Многополюсником называется часть цепи, имеющая более |
|
|
|
двух зажимов. (Пример: взаимная индуктивность). |
|
|
|
Рассмотрим простейший многополюсник с тремя зажимами. |
|
|
|
|
|
||
Как и для любого участка цепи, для него справедливы |
|
|
|
законы Кирхгофа: |
i1 |
|
i2 |
|
|||
i1 i2 i3 0 . |
|
i3 |
|
|
|
|
|
Хотя может показаться не справедливым, что |
три |
|
|
положительных числа в сумме дают ноль, но дело в том, что при записи закона мы можем выбирать произвольное направление токов на рисунке, а уже при расчетах появятся определенные знаки, которые и покажут истинное направление тока. Также справедлив и второй закон Кирхгофа:
U12 U23 U31 0 .
То есть для любого трехполюсника можно задать шесть характеристик, с помощью которых он будет полностью описываться: i 1,i2 ,i3 ,U12 ,U23 ,U31 . Причем, зная четыре из
них, мы всегда можем найти оставшиеся. То есть 4 независимых и 2 зависимых параметра |
|||||
описывают трехполюсник. |
|
|
К |
|
|
Рассмотрим |
конкретный пример трехполюсника, а именно |
|
|
|
|
Б |
|
|
|
||
транзистор. Как известно транзистор имеет базу, эммитор и |
|
|
|
||
|
|
|
|
||
коллектор. Транзистор описывают четыре независимые переменные: |
|
|
|
|
|
iáàç , iêî ë , Uáý , Uêý |
(других быть просто не может). Получаем семейство из |
Uбэ |
|
U |
кэ |
|
|
Э |
|
||
двух вольтамперных характеристик: базовая и коллекторная. |
|
|
|||
|
|
|
|
||
9
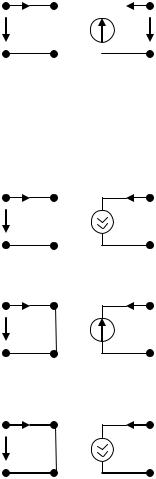
8. Зависимые источники энергии. |
|
|
||
1. Источник ЭДС, управляемый напряжением: |
i1 |
|
i2 |
|
Рассмотрим четырехполюсник, изображенный на рисунке. |
|
|
||
|
|
|||
Можем сказать, что |
i1 0 - разрыв цепи, |
а U2 U1 . U1 |
|
U2 |
Четырехполюсники |
описываются |
матричными |
|
|
|
|
|||
уравнениями, поэтому, чтобы иметь возможность моделировать зависимые источники энергии, запишем полученные уравнения в матричном виде:
|
|
|
|
|
|
|
|
|
0 |
0 U |
|
|
1 |
0 I |
|
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
. |
|
|
|||
|
|
|
|
|
|
|
|
|
|
1 U2 |
0 |
0 I2 |
0 |
|
|
|||||||
2. |
Источник тока, управляемый напряжением: |
|
|
|
i1 |
|||||||||||||||||
|
i1 0 , i2 |
U1 . Это соответствует матричному уравнению: |
|
|||||||||||||||||||
|
|
|
||||||||||||||||||||
|
|
0 |
|
0 |
U |
|
1 |
0 |
I |
|
|
|
0 |
|
|
|
U |
|
||||
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
1 |
||||||
|
|
|
|
0 |
U2 |
0 |
1 |
I2 |
|
|
0 |
|
|
|
|
|
||||||
3. |
Источник ЭДС , управляемый током: |
|
|
|
|
|
|
i1 |
||||||||||||||
|
Ток в первой цепи должен протекать, тогда U1 0 (кинули |
|
||||||||||||||||||||
|
|
|
||||||||||||||||||||
|
закоротку), U2 I1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
U1 |
|||||||
|
|
1 |
|
0 U1 |
|
0 |
0 |
I1 |
|
|
0 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
0 |
|
1 U2 |
|
|
0 |
I2 |
|
|
0 |
|
|
|
|
|
||||||
4. |
Источник тока, управляемый током: |
|
|
|
|
|
|
i1 |
||||||||||||||
|
Это, как раз, наш транзисторный источник тока: |
|
|
|
||||||||||||||||||
|
|
|
|
|
||||||||||||||||||
|
U1 0; I2 |
I1 . Тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
U1 |
||||||
|
|
1 |
0 U |
|
0 |
0 I |
|
|
0 |
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
0 |
0 |
|
|
1 |
|
|
|
I |
1 |
|
|
0 |
|
|
|
|
|
||
|
|
|
U |
2 |
|
1 |
2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Итак, коллекторный ток управляется током, который мы загоняем в базу транзистора. Однако не только источником тока, управляемым током, стоит какая-то физическая модель. Об этом в следующей теме.
i2
 U2
U2
i2
 U2
U2
i2
 U2
U2
10
