
Шпоры / once and for all
.pdf
K |
экв |
K |
|
|
|
R |
|
|
|
|
|||
оу |
оу |
|
|
R |
||
|
|
R |
|
|||
|
|
|
|
н |
||
|
|
|
|
|
|
н |
|
вых |
_ ОУ |
21
R |
экв |
R |
|
|
R |
|
|
вых _ оу |
н |
вых _ ОУ |
|||||
|
|
|
|
22
Билет №5
Вопрос №1
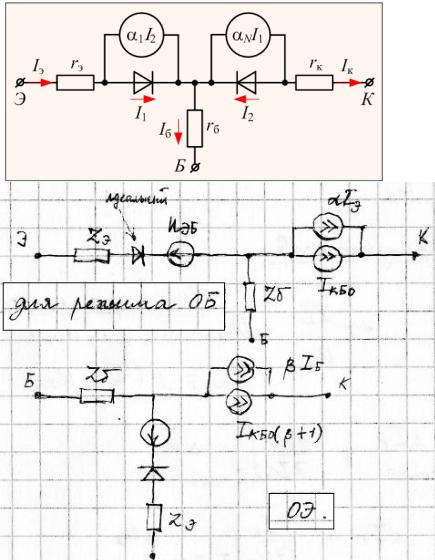
Реальный транзистор при расчете электронных схем можно представить в виде эквивалентной схемы. Здесь оба электронно-дырочных перехода, эмиттерный и коллекторный, представлены диодами VD1 и VD2, а их взаимодействие учитывается
генераторами токов, которые генерируют токи: 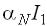 – в нормальном включении (
– в нормальном включении (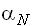 –
–
коэффициент передачи транзистора в нормальном включении); 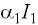 – в инверсном включении. (
– в инверсном включении. (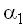 – коэффициент передачи по току в инверсном включении). Собственные сопротивления различных областей транзистора учитываются сопротивлениями:
– коэффициент передачи по току в инверсном включении). Собственные сопротивления различных областей транзистора учитываются сопротивлениями: 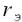 –
–
сопротивление эмиттерной области, 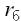 – сопротивление базы,
– сопротивление базы, 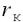 – сопротивление коллектора. Рассмотренная схема, является эквивалентной схемой транзистора по постоянному току, так как не учитывает ряда факторов, оказывающих существенное влияние на переменную составляющую.
– сопротивление коллектора. Рассмотренная схема, является эквивалентной схемой транзистора по постоянному току, так как не учитывает ряда факторов, оказывающих существенное влияние на переменную составляющую.
23
||
||
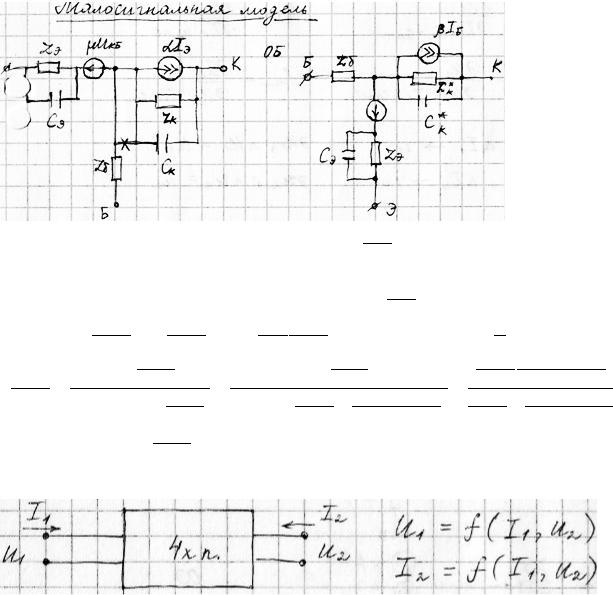
Н-параметры:
|
|
| |
|
|
|
|
|
|
|
|
| |
|
|
|
|
||||||||
|
| |
|
|
|
| |
|
| |
||||
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
| |
|
|
|
|
||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
| |
|
|
|
|
||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
| |
|
|
|
|
||
|
|
|
|
|
|
|
|
||||
24
|
|
|
|
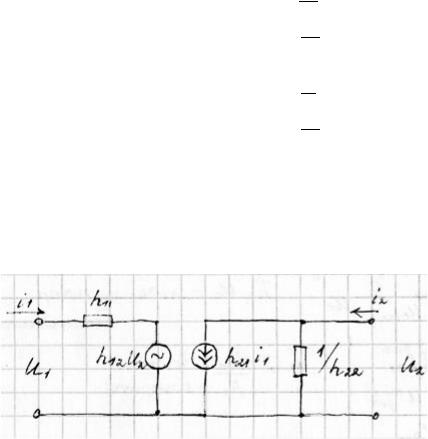
Физ смысл Н-параматров
h11 – вх сопр-е в режиме к.з. выхода
h12 – коэф обр связи по напряжению в режиме хх вх. цепи h21 – коэф передачи входного тока в режиме кз вх цепи h22 – выходная проводимость в режиме хх вых цепи Режим хх и кз д.б. обеспечены только для перем. Сигнала
Для схем с ОБ добавляют индекс б: h11б ОЭ – индекс э.
25
Билет №5
Вопрос №2
Активные RC фильтры. Типы фильтров. Аппроксимация АЧХ ФНЧ. Фильтры Баттерворта и Чебышева.
Электрический фильтр представляет собой частотно-избирательное устройство, пропускающее сигналы в требуемой полосе частот, называемой полосой пропускания, и задерживающее сигналы других частот, относящихся к полосе задерживания. В зависимости от полосы частот прохождения сигнала фильтры с одной полосой пропускания классифицируются на фильтры нижних частот (ФНЧ), верхних частот (ФВЧ) и полосно-пропускающие (полосовые). Существуют и другие типы фильтров, такие, как всепропускающие, частотовыделяющие (узкополосные) и частотоподавляющие (режекторные). Другая классификация фильтров основана на тех положениях теории цепей, по которым они рассчитываются. Она включает фильтры по характеристическим параметрам и фильтры по рабочим параметрам. Также выделяют пассивные и активные фильтры. Примером пассивного фильтра является LC-фильтр, а примером активного – RC-фильтр.
Рассматриваемые активные RC-фильтры относятся к классу линейных электрических цепей с сосредоточенными и постоянными во времени параметрами.
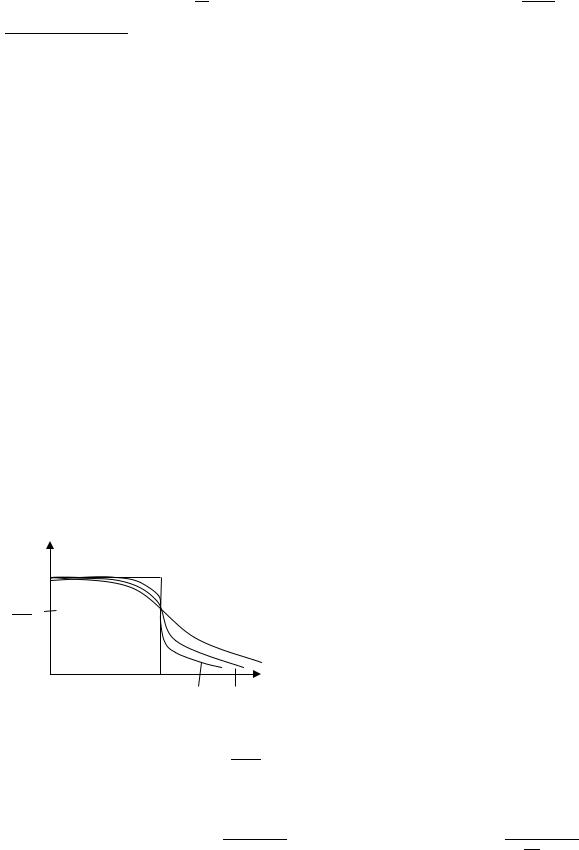
Аппроксимация АЧХ – фильтров.
1) |
|
|
|
- нормирование частоты |
|
|
{
2)Норм. передачи:
M
1
Ω
1
√
{
( )
26
|
|
|
|
|
|
|
∑ |
|
|
|
|
| |
| |
|
|
|
|
| |
| |
|
|
||
|
|
|
|
||||||||
| |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Нужно перейти от | |
| к самому коэффициенту. Для этого приравниваем к 0 |
||||||||||
знаменатель и находим корни. По ним восстанавливаем полиномы Баттерворта.
Полиномы Баттерворта (сомножители степени |
) |
|
|
|
|
n |
|
Сомножители |
1 |
(1+p) |
|
2 |
(1+1,4142p + p2) |
|
3 |
(1+p)(1+p+p2) |
|
4 |
(1+0,7654p+p2)(1+1,847p+p2) |
|
|M|
1
√
 n=2
n=2
1 |
n=6 |
n=4 |
Ω |
|
|
M1
M3 , Ω3

27
√
Чаще всего указывают не значение |M|, а величину a=-20lg(M) ,
По виду полинома, стоящего в знаменателе коэффициента передачи, различают фильтры Баттерворта, Чебышева, Весселя и др.
Фильтры Баттерворта, или фильтры с максимально плоской АЧХ Этот фильтр во многих отношениях обеспечивает определѐнный компромисс. Он
обладает максимально плоской АЧХ в полосе пропускания, но это достигается за счѐт линейности ФЧХ и плавности нарастания затухания. Однако крутизна затухания фильтра Баттерворта достаточно хорошая, и поскольку он обладает приемлемой импульсной характеристикой, обеспечивает отличную универсальную аппроксимацию идеальной характеристики фильтра. Этот фильтр является одним из наиболее употребляемых типов фильтров.
Фильтры Чебышева.
Если же крутизна нарастания затухания, особенно в районе частоты среза, является более важным параметром, чем прямолинейность характеристики в полосе пропускания, то часто используется фильтр с характеристикой Чебышева. Он характеризуется возрастающей длительностью переходного процесса при воздействии на него ступенчатого сигнала и проектируется с заранее определѐнным размахом колебаний коэффициента передачи (т.е. равноволновым) в полосе пропускания, например от 0,01 до 3 дБ. Отсутствие гладкой характеристики в полосе пропускания дает определенные преимущества, а именно обеспечивается высокая скорость нарастания затухания вблизи края полосы пропускания. За исключением диапазона частот, вблизи полосы пропускания характеристическая кривая вне еѐ идѐт параллельно кривой характеристике фильтра Баттерворта эквивалентного порядка.
| |
| |
|
{ |
|
{
| |
Существуют таблицы, как и для Баттерворта.

28
1
n=4
√ |
|
n= |
|
|
Ω
√
1) |
|
- Коэффициент передачи в оп. форме. |
|
∏ |
|||
|
|
2)Максимальная степень полинома в знаменателе коэффициента передачи определяет порядок фильтра.
3)Скорость спада АЧХ за пред. Полосы пропускания nlg20
Как фильтры Баттерворта, так и фильтры Чебышева нижних частот обеспечивают бесконечное затухание только на бесконечной частоте, т.е. вес нули передачи расположены в бесконечности. На любой другой частоте некоторые сигналы будут проходить через фильтр, т.е. даже в полосе задерживания. Если же на неопределѐнной частоте в полосе задерживания требуется бесконечное подавление, то можно использовать характеристику инверсного фильтра Чебышева. В полосе пропускания колебания коэффициента передачи отсутствуют, но они существуют в полосе задерживания, и затухание на определѐнных частотах (так называемых полюсах затухания) становится бесконечным.
Преобразование ФВЧ к ФНЧ
|M|
K(0
ФВЧ
ФНЧ
Ω
(0 - 1)=Ω

29
∏
30
Билет №6
Вопрос №1
Статический режим работы усилительных каскадов. Выбор и стабилизация рабочей точки усилительных каскадов.
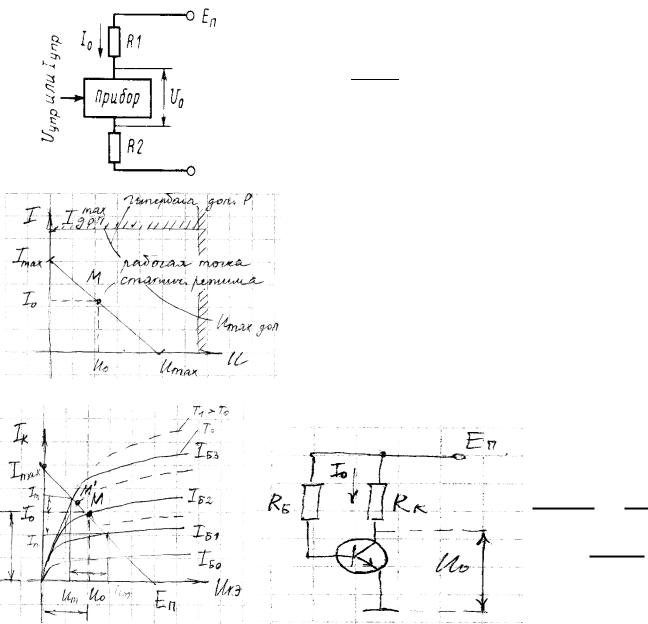
Для корректной работы усилительного каскада его параметры выбирают таким образом, чтобы при отсутствии входного сигнала падала выбранная из определенных соображений величина постоянного U, и протекал постоянный I.
Режим по постоянному току/ статический режим.
1)
2)
График зависимости |
от |
представляет собой |
линию, проходящую через |
и |
|
– линия нагрузки по постоянному току. Для обеспечения статического режима работы
каскада на управляемый вход прибора нужно подать определенную величину I и U – ток и напряжение смещения.
1)
2)
3)
;
;
