15.7. Алгоритмы разбиения области

Во всех алгоритмах разбиения области применяется стратегия «разделяй и властвуй», о которой мы уже говорили при рассмотре-. нии алгоритмов отсечения отрезков прямых и многоугольников. Таким образом, мы отходим от принципов, лежащих в основе пре­дыдущих алгоритмов. Теперь мы будем исследовать область рисунка на картинной плоскости, и те из многоугольников, расположенных в данной области, видимость которых можно определить достаточно «легко», будут изображаться на экране. В противном случае область разбивается на более мелкие области, и процедура принятия реше­ния рекурсивно применяется к каждой из них. По мере того как

размеры области сокращаются, каждую область перекрывает все меньшее и меньшее число многоугольников, так что в конце концов решение будет принято. Очевидно, что при таком подходе работа ведется в пространстве изображения. Этот подход основывается на когерентности области, т. е. считается, что в конечном итоге будут найдены такие области изображения, которые содержат не более одного многоугольника.

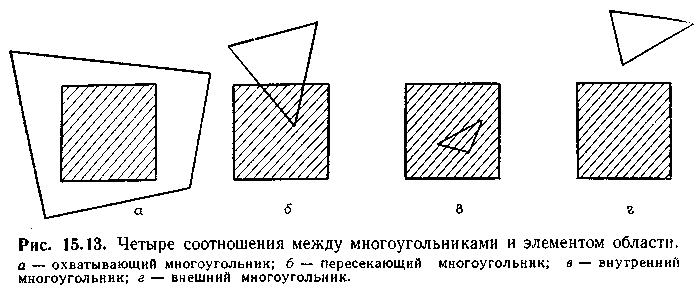
На каждой стадии процесса рекурсивного разбиения проекция каждого многоугольника располагается относительно рассматри­ваемой области одним из следующих четырех способов (рис. 15.13):

а) охватывающие многоугольники полностью включают иссле­дуемую (закрашиваемую) область;

б) пересекающие многоугольники пересекают область;

в) внутренние многоугольники полностью лежат внутри области;

г) внешние многоугольники целиком находятся за пределами об­ласти.

Очевидно, внешние многоугольники не оказывают влияния на область. Можно также не рассматривать ту часть пересекающего многоугольника, которая лежит за пределами области. Другая же часть, находящаяся внутри области, обрабатывается как и вну­тренний многоугольник.

Имеются четыре случая, когда можно непосредственно принять решение относительно области и тем самым прекратить процесс дальнейшего разбиения:

1. Ни один из многоугольников не пересекается с областью, поэтому пэлы области можно окрасить в цвет фона.

2. Имеется либо только один пересекающий многоугольник, либо только один внутренний. Сначала пэлам области присваивается значение фона, а затем многоугольник преобразуется в растровую форму. (На многих дисплеях более удобно вначале весь буфер ре­генерации заполнить значениями фона.) Если многоугольник яв­ляется пересекающим, то растровому преобразованию подвергается лишь та его часть, которая попадает внутрь области.

3. Имеется лишь один-единственный охватывающий многоугольник и нет ни одного пересекающего или внутреннего многоугольника. Пэлам области присваивается значение охватывающего многоуголь­ника.

4. Имеется сразу несколько пересекающих, внутренних и охваты­вающих многоугольников, причем по крайней мере один из них является охватывающим. В этом случае, чтобы определить, распо­ложен ли охватывающий многоугольник впереди всех других мно­гоугольников, применяется простой тест; вычисляются г-коорди-наты плоскостей всех охватывающих, пересекающих и внутренних многоугольников в четырех угловых точках рассматриваемой об­ласти; если существует охватывающий многоугольник, для которого все четыре такие г-координаты меньше (т. е. ближе к точке зрения), чем любые из других вычисленных г-координат, во все пэлы области

можно занести значения, соответствующие охватывающему много­угольнику.

Случаи 1, 2 и 3 обнаруживаются легко. Случай 4 более подробно иллюстрируется на рис. 15.14. На рис. 15.14, а все четыре точки пересечения с охватывающим многоугольником расположены бли­же к точке зрения (которая находится в бесконечности на отрица­тельной полуоси z_v), чем остальные пересечения. Поэтому вся об­ласть закрашивается в цвет охватывающего многоугольника. На рис. 15.14, б, хотя и кажется, что охватывающий многоугольник находится впереди пересекающего, никакого решения принять нель­зя, поскольку слева плоскость пересекающего многоугольника рас­положена перед плоскостью охватывающего многоугольника. От­метим, что алгоритм Ньюэла, Ньюэла и Санча [341] справляется с этим случаем без дальнейшего разбиения области, если пересекаю­щий многоугольник целиком лежит с той стороны от охватываю­щего многоугольника, которая находится дальше от точки зрения. В рассматриваемом же алгоритме для упрощения задачи разбиение области производится всегда.

После того как выполнено разбиение области, необходимо проверить лишь внутренние и пересекающие многоугольники. Ох­ватывающие и внешние многоугольники первоначальной области остаются такими и по отношению к каждой из вновь образованных частей области. Процесс разбиения завершается, когда при умень­шении области достигается разрешение экрана дисплея: при растре

512x512 делается не более девяти разбиений. Если после выпол­нения максимального числа разбиений ни один из рассмотренных выше четырех случаев не обнаруживается, в центре такой недели­мой области размером с пэл вычисляется глубина для всех остав­шихся многоугольников^ Закраску области определяет многоуголь­ник с минимальной координатой г. Кроме того, можно воспользо­ваться несколькими дополнительными уровнями разбиения для устранения лестничного эффекта. При этом определяется такое значение пэла, в котором учитывается сочетание всех видимых в об­ласти многоугольников (разд. 11.7.5).

Первый алгоритм разбиения, предложенный Варноком [484], делил область на четыре квадратные подобласти. На рис. 15.15 показана простая сцена и приведены разбиения, необходимые для ее изображения. Числа, стоящие в каждой из подобластей, соответ­ствуют четырем перечисленным выше случаям завершения процес­са разбиения. Незанумерованные области — это те области, к ко­торым ни один из этих случаев применить нельзя. В данном примере глубина процесса разбиения для большей наглядности ограничена пятью уровнями.

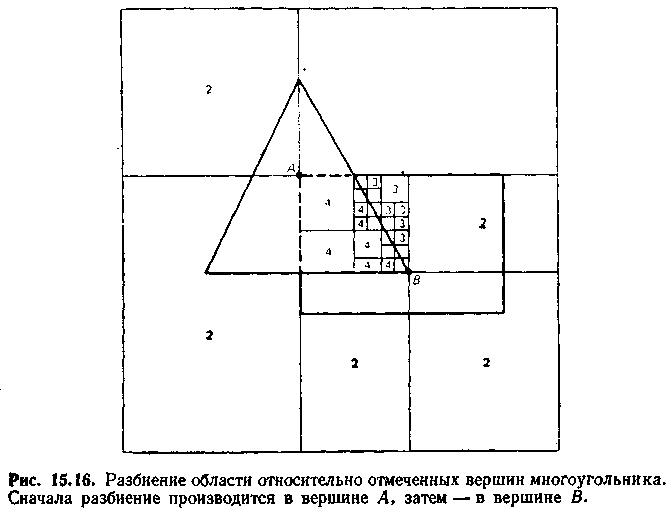
Широко распространенным вариантом разбиения на одинаковые подобласти является разбиение относительно вершины многоуголь­ника (если существует вершина, попадающая в область) (рис. 15.16). Тем самым делается попытка избежать ненужных разбиений.

В другом методе, разработанном Вейлером и Азертоном [490], область экрана разбивается вдоль границ не прямоугольника, а многоугольника. На первом шаге, который не обязателен, но поле­зен для повышения эффективности, производится упорядочение многоугольников в соответствии с некоторым значением z (можно взять минимальную z-координату среди вершин каждого много­угольника). Для начального разбиения, которое выполняется с по­мощью алгоритма, описанного в разд. 11.6.2, выбирается много­угольник, стоящий первым в упорядоченном списке. Например, в случае сцены, показанной на рис. 15.15 и 15.16, был бы взят тре­угольник. Результирующее разбиение прямоугольника на два многоугольника показано на рис. 15.17. Затем, выбирая треуголь­ник в качестве рассматриваемой области и применяя введенную вы­ше терминологию, классифицируем треугольник как охватывающий многоугольник, меньшую часть (А) прямоугольника — как вну­тренний многоугольник, а большую его часть (В) — как внешний многоугольник. После этого обнаруживается случай 4, поскольку охватывающий многоугольник (треугольник) находится далеко впереди внутреннего многоугольника. Поэтому закон закраски треугольника применяется к треугольной области С. По отношению к большей части (В) прямоугольника в качестве охватывающего многоугольника выступает лишь она сама, а два других многоуголь­ника А ч С являются внешними. Это характерно для случая 3, и, следовательно, правило закраски прямоугольника применяется к области В.

Алгоритм разбиения Вейлера—Азертона позволяет резко сокра­тить число разбиений по сравнению с тем, которое требуют два дру­гих метода. Однако в этом алгоритме при каждом разбиении выпол­няется больший объем вычислений, чем в других алгоритмах.